💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 算例1
2.2 算例2
2.3 算例3
2.4 算例4
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
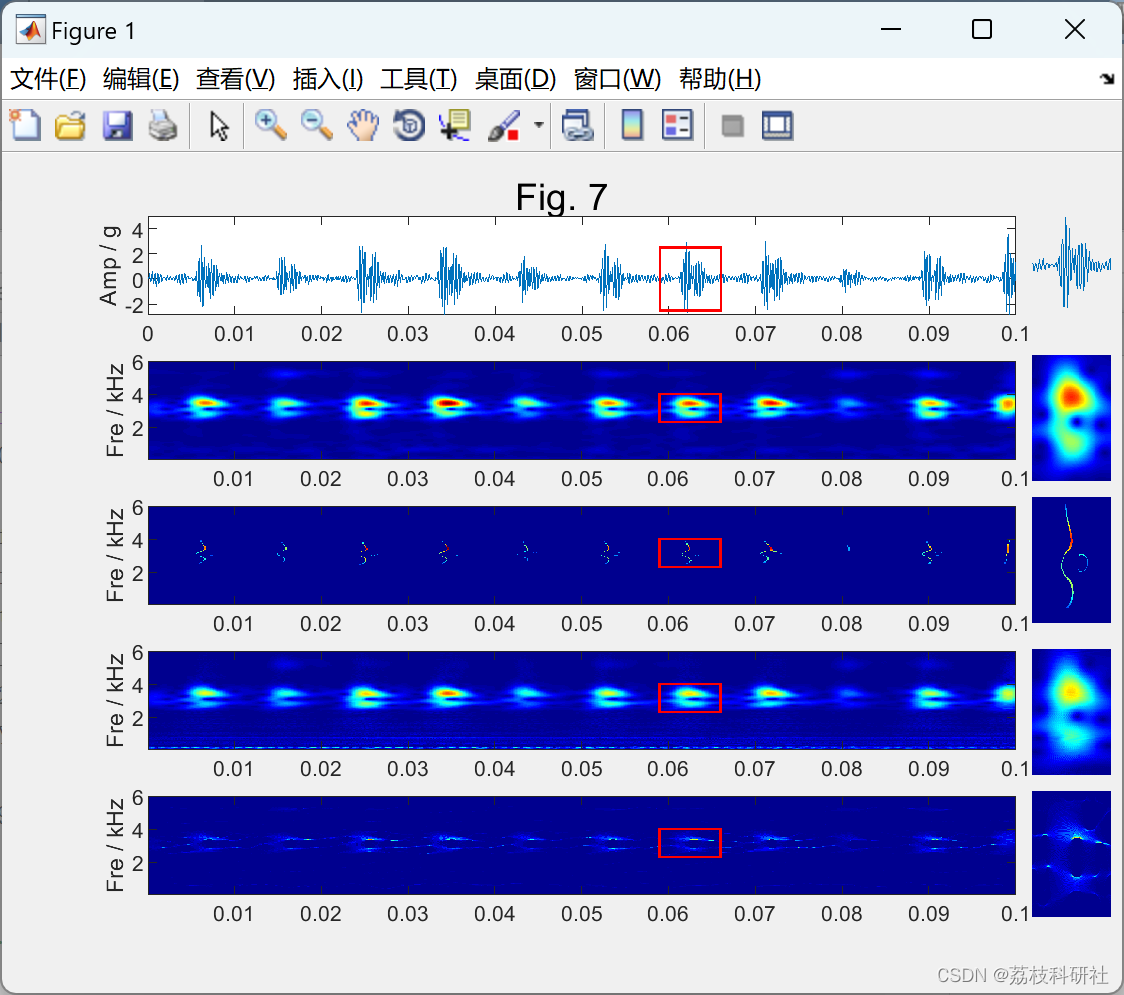
在工业旋转机械中,瞬态信号通常对应于初级元件(例如轴承或齿轮)的故障。然而,面对实际工程的复杂性和多样性,提取瞬态信号是一项极具挑战性的任务。本文提出了一种称为瞬态提取变换的时频分析方法,该方法可以有效地表征和提取故障信号中的瞬态分量。该方法基于短时傅里叶变换,不需要扩展参数或先验信息。采用Rennyi熵和峰度等量化指标将所提方法的性能与其他经典和高级方法进行比较。比较表明,所提方法可以提供能量集中度更高的时频表示,并且可以通过明显更大的峰度提取瞬态分量。数值和实验信号验证了该方法的有效性。
在旋转机械故障诊断领域,广泛应用信号处理方法查找与机械故障密切相关的特征[1],[2]。在记录的振动和声音信号中,故障通常显示短时间内出现的瞬态特征[3]。考虑到不同的故障信号占据不同的频段,联合时频(TF)分析(TFA)是表征具有非平稳TF特征的瞬态故障的有效工具[4]。尽管许多研究报告了TFA方法在故障诊断中的直接应用,但经典TFA方法的固有缺点从未得到有效解决。线性TFA方法,例如短时傅里叶变换(STFT)和小波变换(WT),用于计算信号与具有定位TF特征能力的基函数之间的内积。然而,由于没有可以在TF域中同时紧凑支持的TF基函数,线性TFA方法表征精确TF特征的能力很差。双线性TFA方法,如Wigner-Ville分布和Cohen类分布,用于计算局部信号相关性的傅里叶变换。然而,意外的交叉项极大地限制了双线性TFA方法的应用。经典TFA方法的这些缺点会降低诊断系统对一些不明显故障的敏感性,例如早期的弱故障和被强噪声包围的故障。为了增强TFA方法在复杂环境中检测故障的能力,在过去十年中已经提出并引入了一些先进的方法,例如经验模态分解(EMD)[5],光谱峰度(SK)方法[6],[7]和同步挤压变换(SST)[8]-[10]。
EMD 是一种数据驱动的方法,用于将一维信号分解为一系列固有模式函数 (IMF)。由于不同的IMF占用不同的频段,因此与原始信号相比,包含故障频带的IMF的瞬态特性可以大大增强。由于这种优越性,已经开发了许多基于EMD的故障诊断方法,并在[1]中找到全面的综述。虽然我们不能很好地理解这种方法的数学基础,但一些研究表明,在处理高斯噪声时,EMD表现为二元滤波器组。它表示在执行时间序列信号处理时,EMD 使用固定的二元滤波器组分解信号的因素。由于无法事先知道真实信号中故障分量的频带,因此分解结果是这样的,一些IMF可能包含预期的故障分量,或者一个故障分量可能分解成几个IMF,这通常称为模式混合。由于EMD的处理行为难以控制,有时基于EMD的故障诊断方法不可预测且不稳定。最近,建立了更先进的方法来改善EMD的性能,例如局部均值分解[11],集成EMD [12]和极点加权模态分解[13]。
SK方法是一种基于峰度指标提取最瞬态分量的技术。峰度是用于测量时间序列信号的时间色散的统计变量,也可用于检测故障信号中包含的瞬变。SK方法首先需要基于STFT或带通滤波器将一维信号扩展到二维TF平面,然后重建或选择与峰度最大的断层最相关的分量。得益于峰度指示器对瞬态故障的敏感性,SK方法显示了其在诊断机械故障方面的有效性[1],[2]。
SST方法作为线性TFA方法的后处理工具引入,并已应用于旋转机械的故障诊断[10]。SST旨在获得更清晰的TF表示,可以在高TF分辨率下表征故障。同时,可以从更清晰的TF结果中提取瞬态分量。为了从SST结果中提取信号,必须首先估计与瞬态分量对应的IF轨迹。然而,精确估计瞬态分量的IF具有挑战性,因为故障信号通常不能满足SST框架的弱时变要求。此外,意外的背景噪声会对SST结果造成严重干扰,这可能导致IF无法准确表征。为了进一步提高SST的性能,提出了一些先进的方法,例如解调SST [17],匹配SST [18],高阶SST [19]和同步提取变换(SET)[4]。
从上面的介绍中,我们可以看到,已经引入了许多先进的技术来从原始信号中提取暂态分量,这是提高诊断系统故障检测能力的本质问题。本文提出了一种新的TFA方法,可以精确表征TF平面上的瞬态特征,并在时域中提取。将所提方法与SK、EMD、SST及其改进版本等高级故障诊断方法进行了比较。本文的其余部分组织如下。第二部分详细介绍了我们提出的方法的理论。在第三部分中,使用仁义熵和峰度指标来说明不同TFA方法生成的TF结果的量化比较。实验验证在第四节和第五节中提供。结论见第六节。
📚2 运行结果
2.1 算例1



2.2 算例2
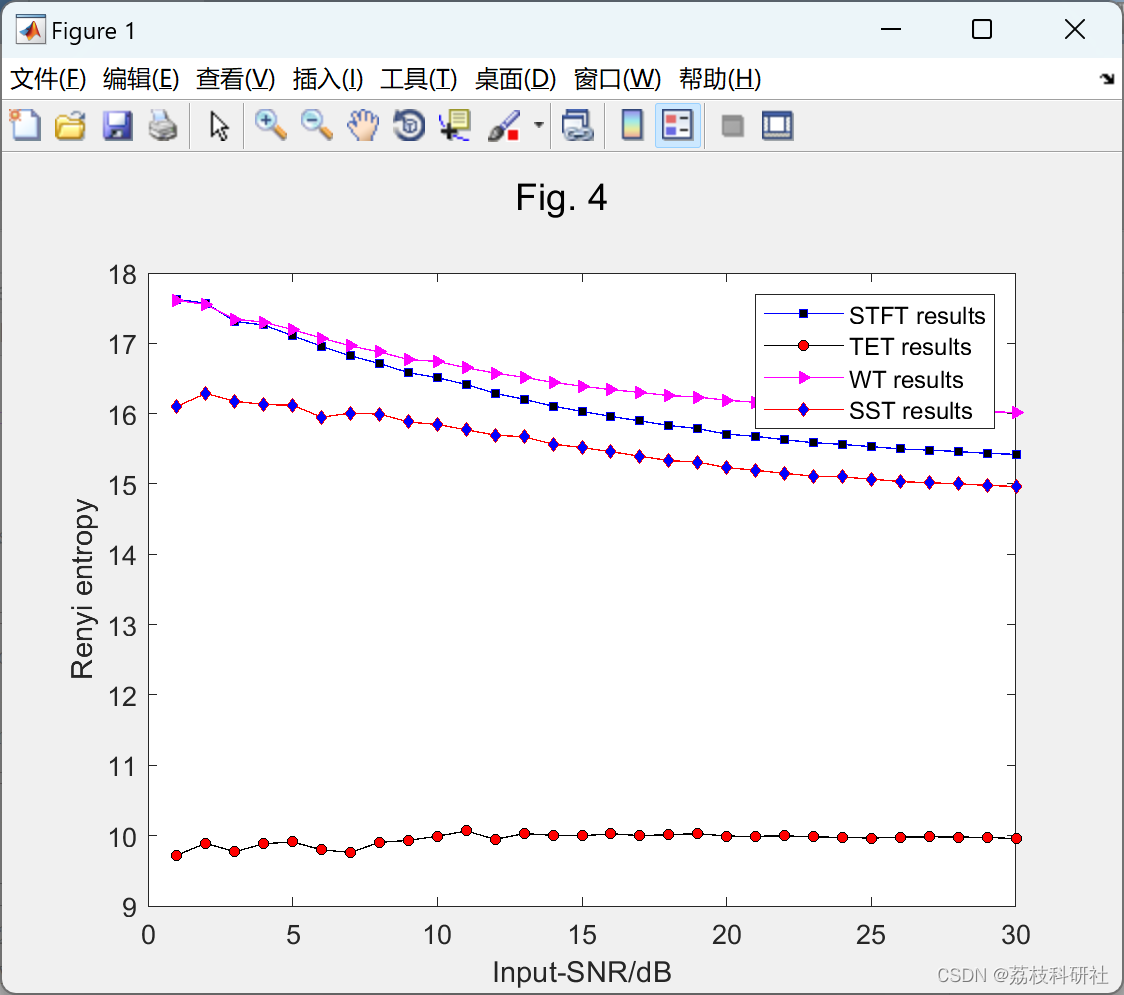


2.3 算例3

2.4 算例4


部分代码:
clear
load('vib_data2.mat')
fs = 12000; N = 1200; % sampling frequency and points
time = (1:N)/fs; % time sequence
fre = (fs/2)/(N/2):(fs/2)/(N/2):(fs/2); % frequency sequence
fre2=fliplr(fre);
data=data(1:N);
[tfr Te]=TET_Y(data,100);
tfr2=WT2(data,fs,600);
Ts=SST_Y(data,100);
x1=0.079; x2=0.083;
y1=2.1; y2=4;
%...................Fig. 12..................................
figure
suptitle('Fig. 12');
subplot(511)
plot(time,data);
axis([0 0.1 -1.25 1.25]);
%xlabel('Time / s');
ylabel('Amp / g');
rectangle('Position',[x1 -1.25 x2-x1 2.5],'EdgeColor','red','Linewidth',1);
axes('position',[0.92,0.815,0.07,0.15]);
plot(time,data);
axis off;
xlim([x1,x2]);ylim([-1.25,2.5]);
subplot(512);
imagesc(time,fre/1000,abs(tfr));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy
colormap jet
rectangle('Position',[x1 y1 x2-x1 y2-y1],'EdgeColor','red','Linewidth',1);
axes('position',[0.92,0.61,0.07,0.15]);
imagesc(time,fre/1000,abs(tfr));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy
colormap jet;
axis off;
%set(ha,'xlim',[x1 x2],'ylim',[y1 y2]);
xlim([x1,x2]);ylim([y1,y2]);
ha=subplot(513);
imagesc(time,fre/1000,abs(Te));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy
colormap jet
rectangle('Position',[x1 y1 x2-x1 y2-y1],'EdgeColor','red','Linewidth',1);
axes('position',[0.92,0.44,0.07,0.15]);
imagesc(time,fre/1000,abs(Te));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy
colormap jet;
axis off;
%set(ha,'xlim',[x1 x2],'ylim',[y1 y2]);
xlim([x1,x2]);ylim([y1,y2]);
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]G. Yu, "A Concentrated Time–Frequency Analysis Tool for Bearing Fault Diagnosis," in IEEE Transactions on Instrumentation and Measurement, vol. 69, no. 2, pp. 371-381, Feb. 2020, doi: 10.1109/TIM.2019.2901514.