文章目录
- 1 什么是粒子群算法?
- 2 举个例子
- 3 还是一个例子
- 算法流程
- 算法实现
- 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 什么是粒子群算法?
粒子群算法(Particle Swarm Optimization,PSO)是一种模仿鸟群、鱼群觅食行为发展起来的一种进化算法。其概念简单易于编程实现且运行效率高、参数相对较少,应用非常广泛。粒子群算法于1995年提出,距今(2019)已有24年历史。
粒子群算法中每一个粒子的位置代表了待求问题的一个候选解。每一个粒子的位置在空间内的好坏由该粒子的位置在待求问题中的适应度值决定。每一个粒子在下一代的位置有其在这一代的位置与其自身的速度矢量决定,其速度决定了粒子每次飞行的方向和距离。在飞行过程中,粒子会记录下自己所到过的最优位置 P,群体也会更新群体所到过的最优位置G 。粒子的飞行速度则由其当前位置、粒子自身所到过的最优位置、群体所到过的最优位置以及粒子此时的速度共同决定。

2 举个例子
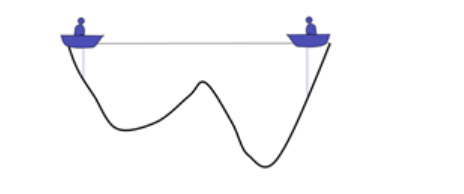
在一个湖中有两个人他们之间可以通信,并且可以探测到自己所在位置的最低点。初始位置如上图所示,由于右边比较深,因此左边的人会往右边移动一下小船。
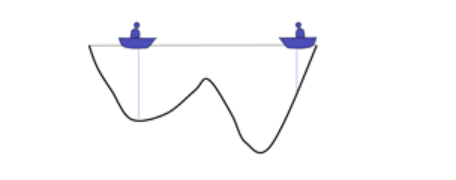
现在左边比较深,因此右边的人会往左边移动一下小船
一直重复该过程,最后两个小船会相遇
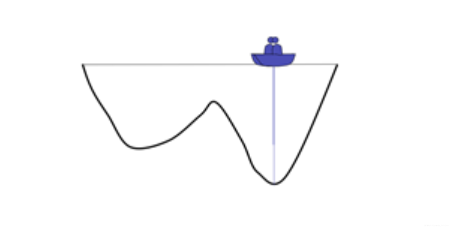
得到一个局部的最优解
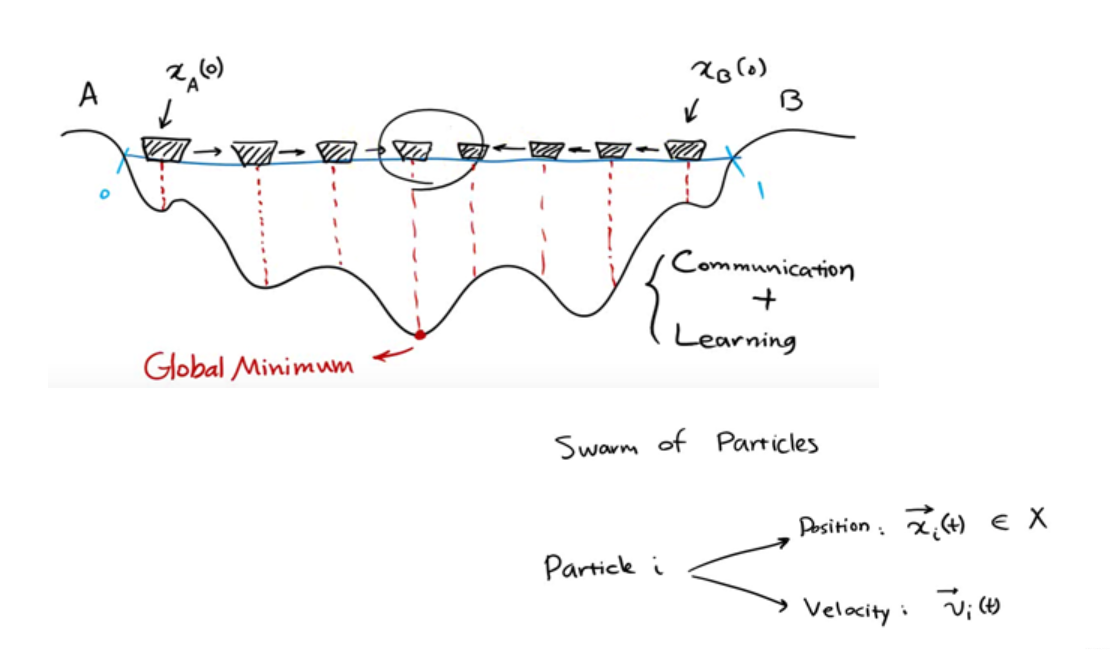 将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
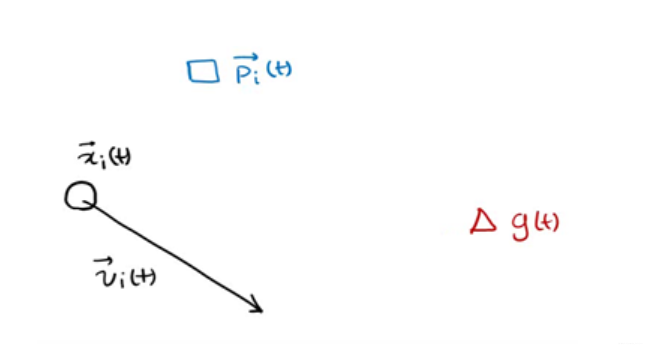
p(t)为在t时刻x个体的自己的最优解,g(t)为在t时刻所有个体的最优解,v(t)为个体在t时刻的方向,x(t)为个体在t时刻的位置
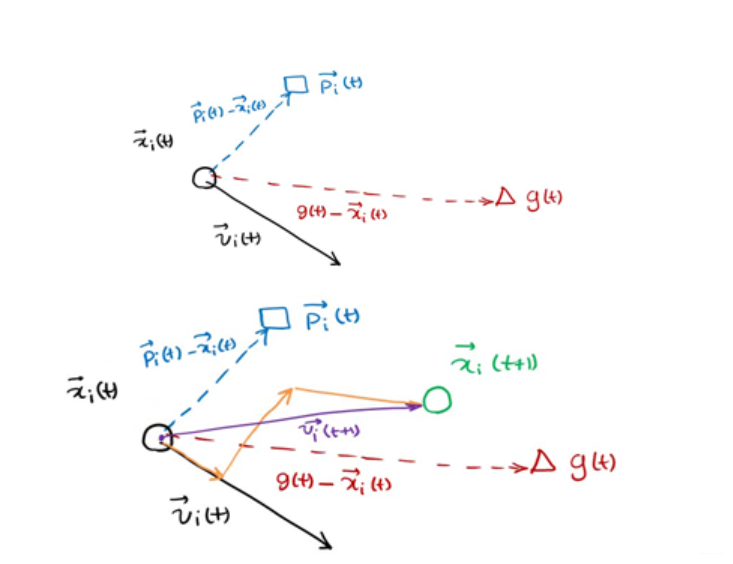
下一个位置为上图所示由x,p,g共同决定了
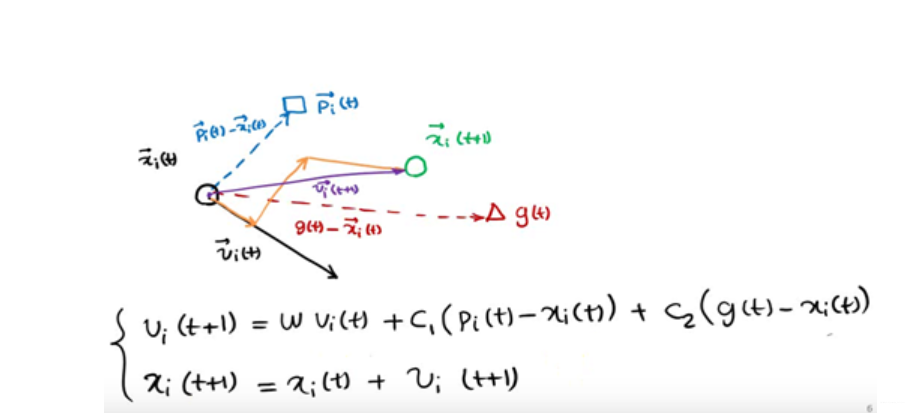
种群中的粒子通过不断地向自身和种群的历史信息进行学习,从而可以找到问题的最优解。
3 还是一个例子
粒子群算法是根据鸟群觅食行为衍生出的算法。现在,我们的主角换成是一群鸟。

小鸟们的目标很简单,要在这一带找到食物最充足的位置安家、休养生息。它们在这个地方的搜索策略如下:
1. 每只鸟随机找一个地方,评估这个地方的食物量。
2. 所有的鸟一起开会,选出食物量最多的地方作为安家的候选点G。
3. 每只鸟回顾自己的旅程,记住自己曾经去过的食物量最多的地方P。
4. 每只鸟为了找到食物量更多的地方,于是向着G飞行,但是呢,不知是出于选择困难症还是对P的留恋,或者是对G的不信任,小鸟向G飞行时,时不时也向P飞行,其实它自己也不知道到底是向G飞行的多还是向P飞行的多。
5. 又到了开会的时间,如果小鸟们决定停止寻找,那么它们会选择当前的G来安家;否则继续2->3->4->5来寻找它们的栖息地。
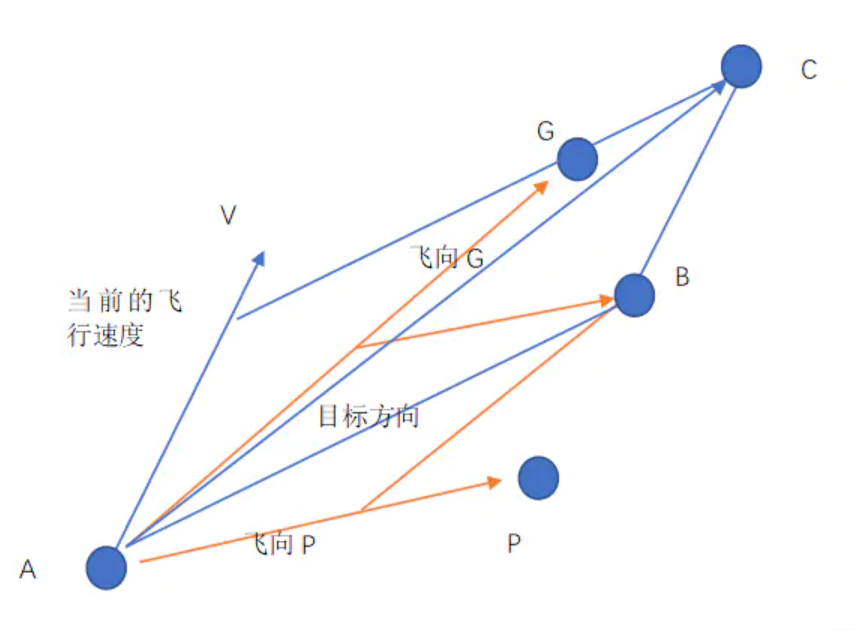
上图描述的策略4的情况,一只鸟在点A处,点G是鸟群们找到过的食物最多的位置,点P是它自己去过的食物最多的地点。V是它现在的飞行速度(速度是矢量,有方向和大小),现在它决定向着P和G飞行,但是这是一只佛系鸟,具体飞多少随缘。如果没有速度V,它应该飞到B点,有了速度V的影响,它的合速度最终使它飞到了点C,这里是它的下一个目的地。如果C比P好那么C就成了下一次的P,如果C比G好,那么就成了下一次的G。
算法流程
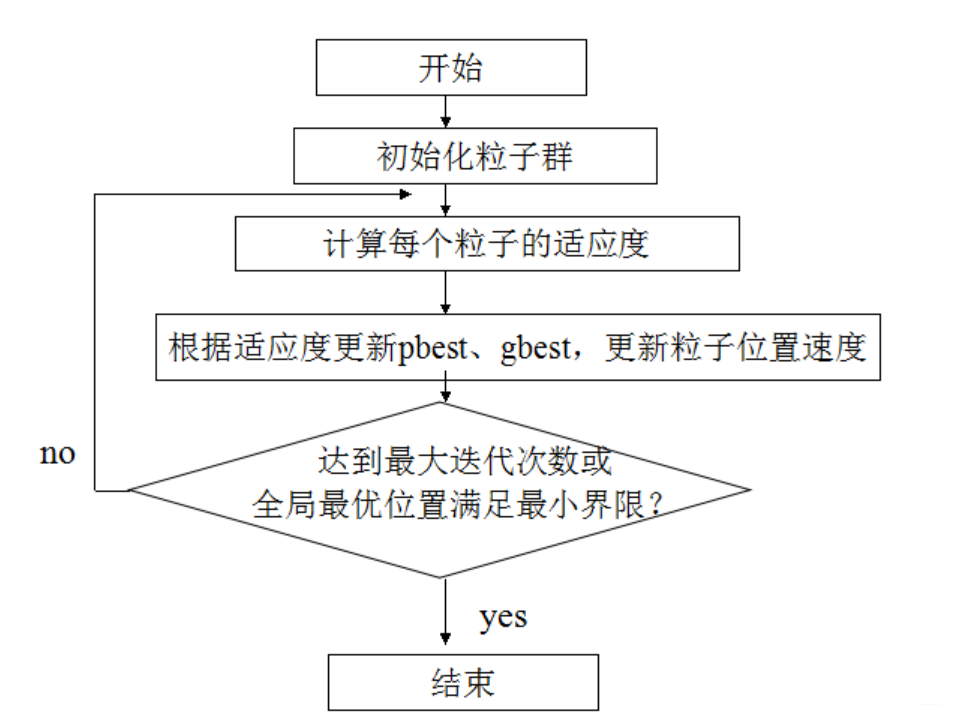
算法实现
这里学长用python来给大家演示使用粒子群解函数最优解
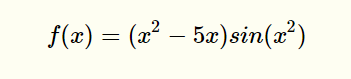
import numpy as np
import matplotlib.pyplot as plt
import random# 定义“粒子”类
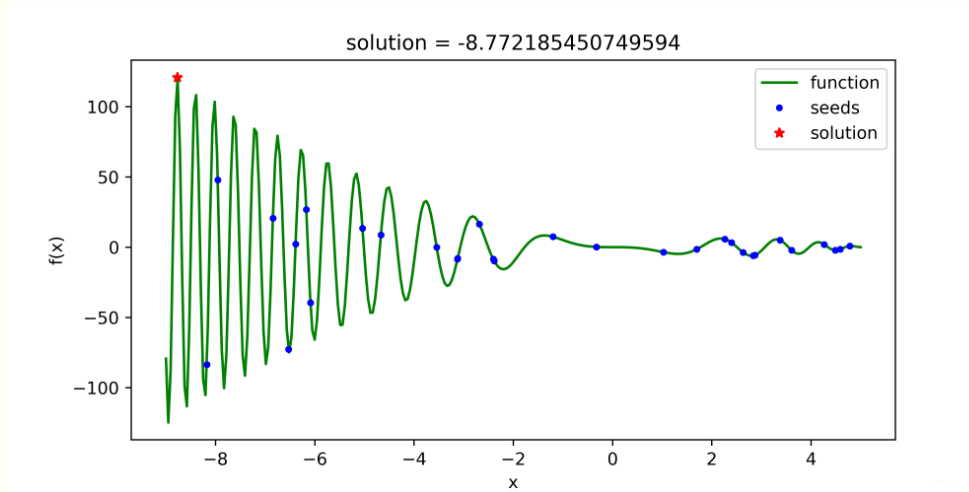
class parti(object):def __init__(self, v, x):self.v = v # 粒子当前速度self.x = x # 粒子当前位置self.pbest = x # 粒子历史最优位置class PSO(object):def __init__(self, interval, tab='min', partisNum=10, iterMax=1000, w=1, c1=2, c2=2):self.interval = interval # 给定状态空间 - 即待求解空间self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值self.iterMax = iterMax # 迭代求解次数self.w = w # 惯性因子self.c1, self.c2 = c1, c2 # 学习因子self.v_max = (interval[1] - interval[0]) * 0.1 # 设置最大迁移速度#####################################################################self.partis_list, self.gbest = self.initPartis(partisNum) # 完成粒子群的初始化,并提取群体历史最优位置self.x_seeds = np.array(list(parti_.x for parti_ in self.partis_list)) # 提取粒子群的种子状态 ###self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def initPartis(self, partisNum):partis_list = list()for i in range(partisNum):v_seed = random.uniform(-self.v_max, self.v_max)x_seed = random.uniform(*self.interval)partis_list.append(parti(v_seed, x_seed))temp = 'find_' + self.tabif hasattr(self, temp): # 采用反射方法提取对应的函数gbest = getattr(self, temp)(partis_list)else:exit('>>>tab标签传参有误:"min"|"max"<<<')return partis_list, gbestdef solve(self):for i in range(self.iterMax):for parti_c in self.partis_list:f1 = self.func(parti_c.x)# 更新粒子速度,并限制在最大迁移速度之内parti_c.v = self.w * parti_c.v + self.c1 * random.random() * (parti_c.pbest - parti_c.x) + self.c2 * random.random() * (self.gbest - parti_c.x)if parti_c.v > self.v_max: parti_c.v = self.v_maxelif parti_c.v < -self.v_max: parti_c.v = -self.v_max# 更新粒子位置,并限制在待解空间之内if self.interval[0] <= parti_c.x + parti_c.v <=self.interval[1]:parti_c.x = parti_c.x + parti_c.velse:parti_c.x = parti_c.x - parti_c.vf2 = self.func(parti_c.x)getattr(self, 'deal_'+self.tab)(f1, f2, parti_c) # 更新粒子历史最优位置与群体历史最优位置def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef find_min(self, partis_list): # 按状态函数最小值找到粒子群初始化的历史最优位置parti = min(partis_list, key=lambda parti: self.func(parti.pbest))return parti.pbestdef find_max(self, partis_list):parti = max(partis_list, key=lambda parti: self.func(parti.pbest)) # 按状态函数最大值找到粒子群初始化的历史最优位置return parti.pbestdef deal_min(self, f1, f2, parti_):if f2 < f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 < self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def deal_max(self, f1, f2, parti_):if f2 > f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 > self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def display(self):print('solution: {}'.format(self.gbest))plt.figure(figsize=(8, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seeds, self.func(self.x_seeds), 'b.', label='seeds')plt.plot(self.gbest, self.func(self.gbest), 'r*', label='solution')plt.xlabel('x')plt.ylabel('f(x)')plt.title('solution = {}'.format(self.gbest))plt.legend()plt.savefig('PSO.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':PSO([-9, 5], 'max')
效果
建模资料
资料分享: 最强建模资料