目录
1 从2元一次方程组求解说起
1.1 直接用方程组消元法求解
1.2 有没有其他方法呢?有:比如2阶行列式方法
1.3 3阶行列式
2 行列式的定义
2.1 矩阵里的方阵
2.2 行列式定义:返回值为标量的一个函数
2.3 行列式的计算公式
2.4 克拉默法则
2.4.1 克拉默法则的内容
2.4.2 克拉默法则 对行列式的展开公式
2.4.3 克拉默法则,行列式展开式的由来
2.4.3.1 全排列
2.4.3.2逆序数
2.4.3.3 行列式展开为 Σ逆序数* 每一种排列
3 行列式的意义
3.1 基础定义?
3.2 几何意义
3.3 行列式的意义和作用呢?
3.4 行列式的结果(是1个标量)的作用
10 扩展话题:行列式与模(未完成)
1 从2元一次方程组求解说起
1.1 直接用方程组消元法求解
- 我们都学过多元一次方程组
- 一般来说,要求解n元方程组,意味着至少需要n个方程组成的方程组才可以
- 求解常规的是可以采用消元法,带入其他方程组,缩减方程组复杂度而逐步求解
。。。
继续代入,消元后求解最终得到
1.2 有没有其他方法呢?有:比如2阶行列式方法
因为二阶行列式的公式求值如下
所以二元方程组的求解也可以用行列式写成
1.3 3阶行列式
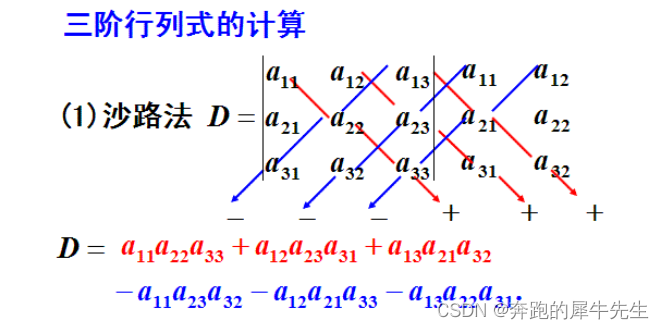

2 行列式的定义
2.1 矩阵里的方阵
- 矩阵里,行数=列数的矩阵叫做方阵
- 方阵有很多很好的特殊属性
- 只有方阵才有逆矩阵
- 只有方阵才有行列式,因为行列式要求 行数=列数
2.2 行列式定义:返回值为标量的一个函数
- 它的定义域是det的矩阵A,并且行列式也可以看作是一般欧氏空间中有向面积或体积概念的推广。或者说,在N维欧氏空间中,行列式描述了一个线性变换对“体积”的影响。
- 行列式是数学中的一个函数,是定义域为det的矩阵A的函数
- 其值为标量,
- 记为det(A)或|A|
2.3 行列式的计算公式
- 上面列举了2阶和3阶行列式的展开公式
- 但是为什么是这样的呢?
- 其实这里要涉及 余子式的概念,和克拉默法则
2.4 克拉默法则
2.4.1 克拉默法则的内容
- 线性方程组 Ax=b ,如果系数矩阵A是满秩的方阵,那么多元一次方程组的解可以写成如下展开公式,其中参数为行列式
- 下面列举得是:2阶行列式和3阶行列式


克拉默法则
- 分母都是系数矩阵A的行列式 |A|
- 分子是对系数矩阵A做了一些修改的行列式,比如求xi 就把第i 列替换为 结果b列(b列实际挪到等号左边就是 常数项列)
2.4.2 克拉默法则 对行列式的展开公式
2阶行列式的展开式
2阶行列式的展开式

2.4.3 克拉默法则,行列式展开式的由来
2.4.3.1 全排列
- 根据排列公式即可知道
- 比如3个数字的排列种类有 p(3)=3*2*1=6种
2.4.3.2逆序数
- 数组中某个位置的数字的逆序数:数组里如果某个元素比它前面某个元素小,就记为1个逆序,如果有多个则累加。如果比它前面所有元素都大,则逆序数记为0
- 数组的逆序数:一个数组排列中,所有位置上的数的逆序数的总和称为该数组的逆序数。
- 数组的逆序数的奇偶性:如果这个总数是奇数就是奇书
- 一个数组/序列内某个位置的数的逆序数,ti是按每个数组内元素的位置,分别求的
- 没有逆序数,记为0
- 有逆序数,记为逆序数的个数
- 比如 1,3,2 其逆序数 t1=0, t2=0, t3=1(只看第3个数之前的数 和 第3个数的大小)
- 而这些每个元素的逆序数求和就是,这个数组的逆序数Σti
2.4.3.3 行列式展开为 Σ逆序数* 每一种排列
|A| = Σ逆序数* 每一种排列

3 行列式的意义
3.1 基础定义?
- 行列式是方阵的一种特殊运算
- 如果矩阵行数列数相等,那么这个矩阵是方阵。只有方阵才有行列式
- 行列数的计算方式和矩阵的不同
3.2 几何意义
- 行列式其实是,矩阵变化的一个面积变化比率!
- 如果是2维的,行列数的值代表 有向面积的变化率/变化倍数
- 如果是3维的,行列数的值表示体积变化的系数


3.3 行列式的意义和作用呢?
- 作用1:快速解出,多元方程组的解
- 作用2:通过矩阵的余子式的转置等计算,矩阵的逆矩阵
3.4 行列式的结果(是1个标量)的作用
- 行列数的值代表 有向面积的变化率/变化倍数
- 行列式的值(结构)的作用
- |A| =|AT| 矩阵和对应转置矩阵的行列式相等
- 如果 |A|≠0 ,则,矩阵A满秩,矩阵A可逆
- 如果 |A|=0 ,那么就是说至少有两个向量在变换之后,共线了。参考[1,1;1,1] 矩阵的效果
- 如果 |A|>0 ,正值表示方向相同
- 如果 |A|<0 ,负值代表着翻面了,方向相反,相对位置发生了调换
10 扩展话题:行列式与模(未完成)
一版情况下,我就认为 行列式就是带符号的矩阵的模
什么是矩阵的模_百度知道https://zhidao.baidu.com/question/122421786.html向量的行列式和向量的模一样吗? - 知乎真可以这么看,行列式就是矩阵的模。其实,用“模”这个字比用“行列式”这个词更贴近“行列式”要描述的…
![]() https://www.zhihu.com/question/505441153/answer/2269396667?utm_id=0
https://www.zhihu.com/question/505441153/answer/2269396667?utm_id=0



![java八股文面试[JVM]——元空间](https://img-blog.csdnimg.cn/90f722c77387484e86ba08c552ba2538.png)