相关系数

相关性分析的关键是计算相关系数，在本节课中将会介绍两种常用的相关系数：皮尔逊相关系数（Pearson）和斯皮尔曼相关系数（Spearman）。

它们可以用来衡量两个变量间相关性的大小，对于不同类型的数据，我们要用不同的相关系数进行计算分析。

统计学概念

在学习这两个系数之前，我们需要了解一些必要的概率统计中的概念，以便于公式的理解和推导。

总体	所要考察对象的全部个体
样本	从总体中抽取的一部分个体

为了对考察对象进行分析，我们总是希望得到总体数据的一些特征，例如均值、方差、标准差等；

但总体数据往往过多，以致于难以进行计算，因此我们可以计算从从总体中抽取的样本的统计量，以此来估计总体的统计量。

皮尔逊相关系数

总体皮尔逊相关系数

X和Y的变化方向相同：当X大于其均值时，Y也大于其均值，当X小于其均值时，Y也小于其均值

协方差的本质：若X和Y的变化方向相同，则协方差为正；若X和Y的变化方向相反，则协方差为负；若X和Y的变化方向无关联，则协方差正负抵消为零。

注意：协方差的大小和两个变量的量纲有关，因此不适合做比较。

皮尔逊相关系数的本质：可以看作剔除了两个变量量纲影响、将X和Y标准化后的协方差。

样本皮尔逊相关系数

 相关系数可视化

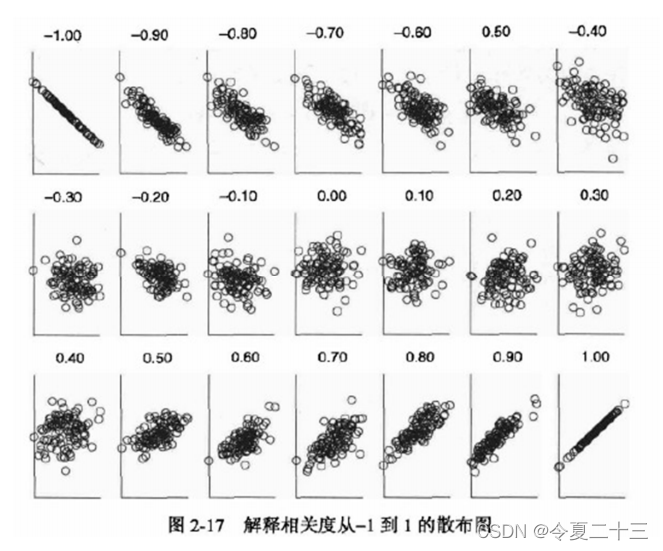
在计算相关系数之前，需要通过绘制散点图来判断X和Y之间的相关性，如果散点图显示二者不相关，那么计算出的相关系数也就没有意义了。

只有先确定两个变量是线性相关的，相关系数才能告诉我们这两个变量的相关程度如何。

  事实上，比起相关系数的大小，我们往往更关注的是其显著性，这就需要进行假设检验。

对皮尔逊相关系数进行假设检验

进行假设检验可以判断我们所求得的皮尔逊相关系数是否准确，若检验结果越显著，就表示我们求得的相关系数越不准确。

第一步：提出原假设和备择假设，两者是截然相反的；如果我们已经计算得到了一个皮尔逊相关系数，我们要检验它是否显著异于0，则可以设定原假设和备择假设为：H0：r=0    H1：r≠0

第二步：在原假设成立的条件下，利用我们要检验的量构造出一个符合某一分布的统计量

第三步：将我们要检验的值带入统计量中，可以得到一个特定的检验值

第四步：我们可以根据统计量的分布绘制一个概率密度函数图像，并给定一个置信水平，一般为95%，根据这个置信水平查找到临界值，并画出检验统计量的接受域和拒绝域

第五步：看我们计算出来的检验值是落在了接受域还是拒绝域，并下结论。

皮尔逊相关系数假设检验的条件

第一，实验数据通常是成对地来自于正态分布的总体；

第二，实验数据之间的差距不能太大，皮尔逊相关系数受异常值的影响比较大；

第三，每组样本之间是独立抽样的。

从上面可以知道，我们需要正态分布的数据，才可以进行假设检验，所以我们还需要进行正态分布检验。

正态分布检验使用的方法是JB检验，JB检验也是一个假设检验的过程。

若实验数据足够多，那我们就可以使用Q-Q图来检验，只要图上的点近似地在一条直线附近，我们就可以说样本数据近似于正态分布。

斯皮尔曼相关系数

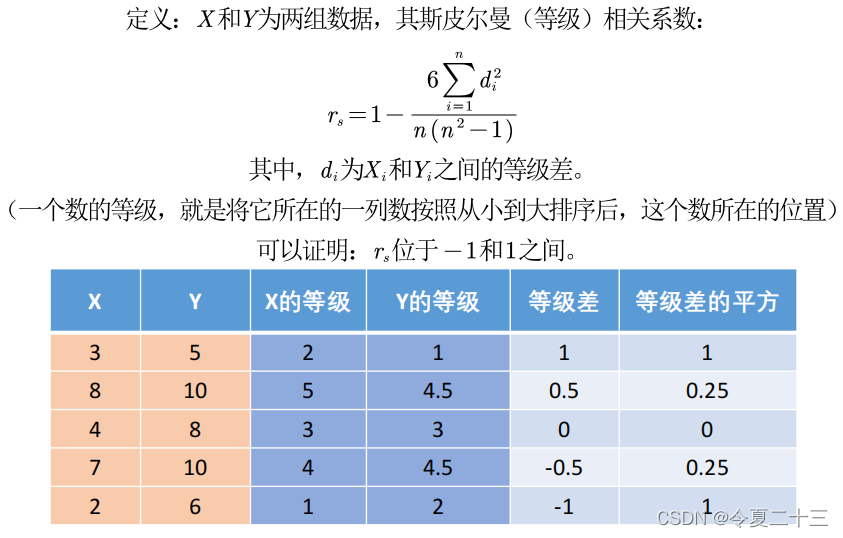
对斯皮尔曼相关系数也要进行假设检验。

两个相关系数的比较