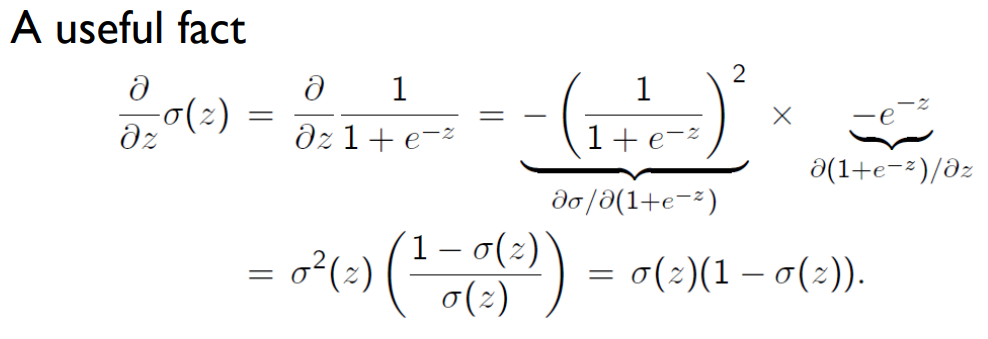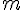文章目录
- 逻辑回归分类
- Logistic Regression Classification
- Logistic Regression: Log Odds
- Logistic Regression: Decision Boundary
- Likelihood under the Logistic Model
- Training the Logistic Model
- Gradient Descent
逻辑回归分类
考虑二分类问题,其中每个样本由一个特征向量表示。
直观理解:将特征向量 x \text{x} x映射到一个实数 w T x \text{w}^T\text{x} wTx
- 一个正的值 w T x \text{w}^T\text{x} wTx表示 x \text{x} x属于正类的可能性较高。
- 一个负的值 w T x \text{w}^T\text{x} wTx表示 x \text{x} x属于负类的可能性较高。
概率解释: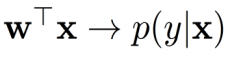
- 对映射值应用一个变换函数,将其范围压缩在0和1之间。
- 变换后的值表示属于正类的概率。
- 变换后的值 w T x ∈ ( − ∞ , + ∞ ) \text{w}^T\text{x}\in(-∞,+∞) wTx∈(−∞,+∞)的范围是 [ 0 , 1 ] [0, 1] [0,1]。
注意:在逻辑回归中通常使用的变换函数是sigmoid函数。
Logistic Regression Classification
条件概率:
- 条件概率在分类任务中很重要。
- 使用逻辑函数(也称为sigmoid函数)计算条件概率。
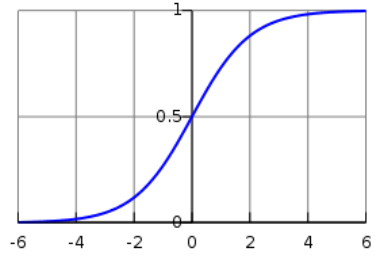
逻辑函数 / sigmoid函数:
-
当 z 趋近正无穷时,逻辑函数趋近于1。
-
当 z 趋近负无穷时,逻辑函数趋近于0。
-
当 z = 0 时,逻辑函数等于0.5,表示两个类别的概率相等。
-
给定输入 x,正类的概率表示为:
p ( y = 1 ∣ x ) = σ ( w T x ) = 1 1 + e − w T x = e w T x 1 + e w T x p(y = 1 \,|\, x) =\sigma(w^Tx) = \cfrac{1}{1 + e^{-w^T x}} = \cfrac{e^{w^T x}}{1 + e^{w^T x}} p(y=1∣x)=σ(wTx)=1+e−wTx1=1+ewTxewTx -
给定输入 x,负类的概率表示为:
p ( y = 0 ∣ x ) = 1 − p ( y = 1 ∣ x ) = 1 1 + e w T x p(y = 0 \,|\, x) = 1 - p(y = 1 \,|\, x) = \cfrac{1}{1 + e^{w^T x}} p(y=0∣x)=1−p(y=1∣x)=1+ewTx1
Logistic Regression: Log Odds
- 在逻辑回归中,我们使用log odds(对数几率)来建模。
- 一个事件的几率(odds):该事件发生的概率与不发生的概率的比值, p 1 − p \cfrac{p}{1-p} 1−pp。
- log odds / logit function: log ( p 1 − p ) \log\left(\cfrac{p}{1-p}\right) log(1−pp)。
- Log odds for logistic regression: log ( p ( y = 1 ∣ x ) 1 − p ( y = 1 ∣ x ) ) = w T x \log\left(\cfrac{p(y=1|x)}{1-p(y=1|x)}\right) = w^Tx log(1−p(y=1∣x)p(y=1∣x))=wTx。
在逻辑回归中,我们通过学习适当的权重 w w w 来建立一个线性模型,该模型可以将输入特征 x x x 映射到对数几率(log odds)上。然后,通过对对数几率应用逻辑函数(sigmoid函数)来得到分类概率。
Logistic Regression: Decision Boundary
决策边界: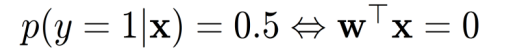
- 在逻辑回归中,决策边界是指分类模型对于输入特征的判断边界。
- 对于线性逻辑回归模型,决策边界是线性的。
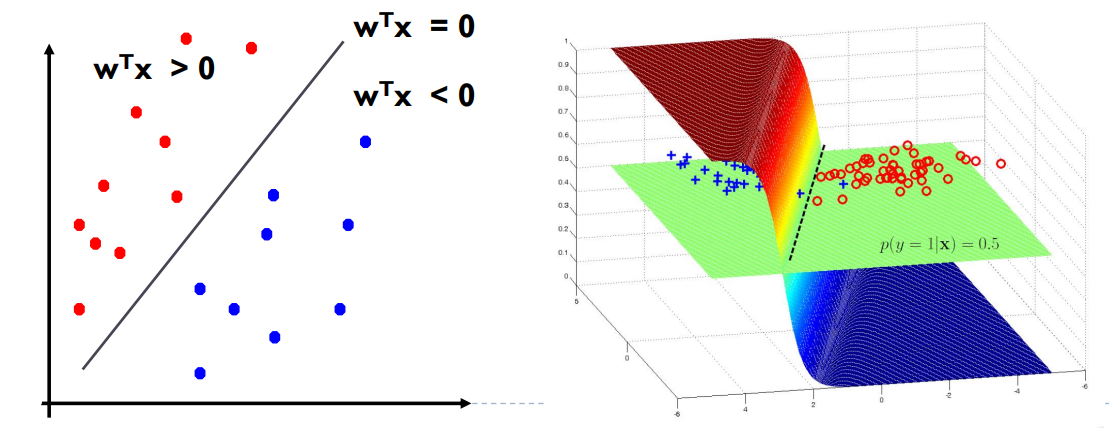
决策规则:
- 如果 p ^ ( y = 1 ∣ x ) ≥ 0.5 \hat{p}(y=1|x) \geq 0.5 p^(y=1∣x)≥0.5,则预测为正类。
- 如果 p ^ ( y = 1 ∣ x ) < 0.5 \hat{p}(y=1|x) < 0.5 p^(y=1∣x)<0.5,则预测为负类。
对于线性逻辑回归,决策边界是一个线性函数,用于将特征空间划分为两个不同的类别区域。
Likelihood under the Logistic Model
在逻辑回归中,我们观察标签并测量它们在模型下的概率。
给定参数 w w w,样本的条件对数似然函数为:
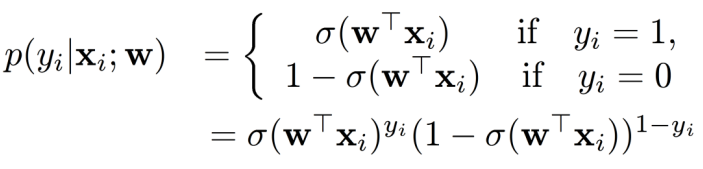
对数似然函数的表达式为:
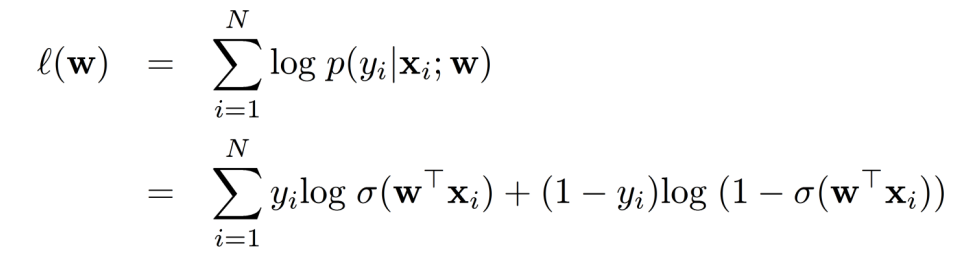
其中, N N N 是样本数量, x i x_i xi 是第 i i i 个样本的特征向量, y i y_i yi 是第 i i i 个样本的标签。
通过最大化对数似然函数来估计参数 w w w,可以找到最佳的参数值,使得模型的概率预测与观察到的标签尽可能一致。
Training the Logistic Model
训练逻辑回归模型(即找到参数 w w w)可以通过最大化训练数据的条件对数似然函数或最小化损失函数来完成。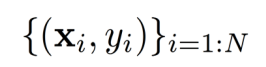
最大化条件对数似然函数 or 最小化损失函数:
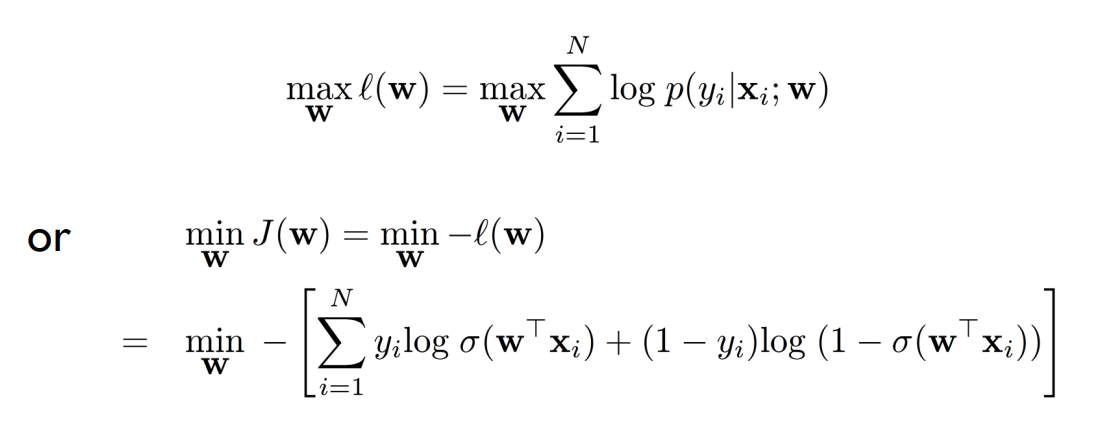
其中, N N N 是训练数据的样本数量, x i x_i xi 是第 i i i 个样本的特征向量, y i y_i yi 是第 i i i 个样本的标签。
通过最大化条件对数似然函数或最小化损失函数,我们可以找到最优的参数 w w w,使得模型能够最好地拟合训练数据,并能够准确地预测新的样本标签。常用的优化算法,如梯度下降法或牛顿法,可以用于求解最优参数。
Gradient Descent
梯度下降是一种常用的优化算法,用于求解最小化损失函数的问题。
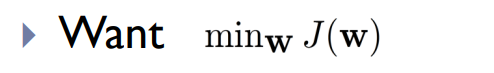
梯度下降的步骤如下:
- 初始化参数 w w w 的值。
- 重复以下步骤直到满足停止条件:
- 计算损失函数 J ( w ) J(w) J(w) 对参数 w w w 的梯度,即 ∂ J ( w ) ∂ w \cfrac{\partial J(w)}{\partial w} ∂w∂J(w)。
- 根据学习率 α \alpha α,更新参数 w w w 的值: w j : = w j − α ∂ J ( w ) ∂ w j w_j := w_j - \alpha \cfrac{\partial J(w)}{\partial w_j} wj:=wj−α∂wj∂J(w),对所有参数 w j w_j wj 同时进行更新。
梯度下降的目标是通过迭代更新参数,逐渐减小损失函数的值,直到达到局部最小值或收敛。
在逻辑回归中,我们可以使用梯度下降算法来最小化损失函数 J ( w ) J(w) J(w),从而找到最优的参数 w w w,使得模型能够最好地拟合训练数据。通过计算损失函数对参数的梯度,然后根据梯度和学习率更新参数,我们可以逐步调整参数的值,使得损失函数逐渐减小,从而达到最优参数的目标。