Every day a Leetcode
题目来源:130. 被围绕的区域
本题给定的矩阵中有三种元素:
- 字母 X;
- 被字母 X 包围的字母 O;
- 没有被字母 X 包围的字母 O。
本题要求将所有被字母 X 包围的字母 O都变为字母 X ,但很难判断哪些 O 是被包围的,哪些 O 不是被包围的。
注意到题目解释中提到:任何边界上的 O 都不会被填充为 X。 我们可以想到,所有的不被包围的 O 都直接或间接与边界上的 O 相连。
我们可以利用这个性质判断 O 是否在边界上,具体地说:
对于每一个边界上的 O,我们以它为起点,标记所有与它直接或间接相连的字母 O;
最后我们遍历这个矩阵,对于每一个字母:
- 如果该字母被标记过,则该字母为没有被字母 X 包围的字母 O,我们将其还原为字母 O;
- 如果该字母没有被标记过,则该字母为被字母 X 包围的字母 O,我们将其修改为字母 X。
解法1:深度优先搜索
我们可以使用深度优先搜索实现标记操作。
在下面的代码中,我们把标记过的字母 O 修改为字母 A。
代码:
/** @lc app=leetcode.cn id=130 lang=cpp** [130] 被围绕的区域*/// @lc code=start
class Solution
{
public:// 主函数void solve(vector<vector<char>> &board){if (board.empty())return;int m = board.size(), n = m ? board[0].size() : 0;for (int i = 0; i < m; i++){dfs(board, i, 0);dfs(board, i, n - 1);}for (int j = 0; j < n; j++){dfs(board, 0, j);dfs(board, m - 1, j);}for (int i = 0; i < m; i++)for (int j = 0; j < n; j++){if (board[i][j] == 'A')board[i][j] = 'O';else if (board[i][j] == 'O')board[i][j] = 'X';}}// 辅函数void dfs(vector<vector<char>> &board, int x, int y){int m = board.size(), n = m ? board[0].size() : 0;if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O')return;board[x][y] = 'A';dfs(board, x + 1, y);dfs(board, x - 1, y);dfs(board, x, y + 1);dfs(board, x, y - 1);}
};
// @lc code=end
结果:
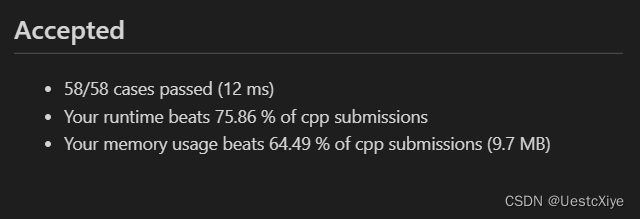
复杂度分析:
时间复杂度:O(n×m),其中 n 和 m 分别为矩阵的行数和列数。深度优先搜索过程中,每一个点至多只会被标记一次。
空间复杂度:O(n×m),其中 n 和 m 分别为矩阵的行数和列数。主要为深度优先搜索的栈的开销。
解法2:广度优先搜索
我们可以使用广度优先搜索实现标记操作。在下面的代码中,我们把标记过的字母 O 修改为字母 A。
代码:
/** @lc app=leetcode.cn id=130 lang=cpp** [130] 被围绕的区域*/// @lc code=start// DFS
// class Solution
// {
// public:
// // 主函数
// void solve(vector<vector<char>> &board)
// {
// if (board.empty())
// return;
// int m = board.size(), n = m ? board[0].size() : 0;
// for (int i = 0; i < m; i++)
// {
// dfs(board, i, 0);
// dfs(board, i, n - 1);
// }
// for (int j = 0; j < n; j++)
// {
// dfs(board, 0, j);
// dfs(board, m - 1, j);
// }
// for (int i = 0; i < m; i++)
// for (int j = 0; j < n; j++)
// {
// if (board[i][j] == 'A')
// board[i][j] = 'O';
// else if (board[i][j] == 'O')
// board[i][j] = 'X';
// }
// }
// // 辅函数
// void dfs(vector<vector<char>> &board, int x, int y)
// {
// int m = board.size(), n = m ? board[0].size() : 0;
// if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O')
// return;
// board[x][y] = 'A';
// dfs(board, x + 1, y);
// dfs(board, x - 1, y);
// dfs(board, x, y + 1);
// dfs(board, x, y - 1);
// }
// };// BFS
class Solution
{
private:vector<int> direction{-1, 0, 1, 0, -1};public:// 主函数void solve(vector<vector<char>> &board){if (board.empty())return;int m = board.size(), n = m ? board[0].size() : 0;queue<pair<int, int>> q;// 从最外围开始,初始化队列for (int i = 0; i < m; i++){if (board[i][0] == 'O'){q.push(pair<int, int>{i, 0});board[i][0] = 'A';}if (board[i][n - 1] == 'O'){q.push(pair<int, int>{i, n - 1});board[i][n - 1] = 'A';}}for (int j = 0; j < n; j++){if (board[0][j] == 'O'){q.push(pair<int, int>{0, j});board[0][j] = 'A';}if (board[m - 1][j] == 'O'){q.push(pair<int, int>{m - 1, j});board[m - 1][j] = 'A';}}// BFS遍历while (!q.empty()){auto [r, c] = q.front();q.pop();for (int k = 0; k < 4; k++){int x = r + direction[k], y = c + direction[k + 1];if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O')continue;q.push(pair<int, int>{x, y});board[x][y] = 'A';}}// 最终修改for (int i = 0; i < m; i++)for (int j = 0; j < n; j++){if (board[i][j] == 'A')board[i][j] = 'O';else if (board[i][j] == 'O')board[i][j] = 'X';}}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(n×m),其中 n 和 m 分别为矩阵的行数和列数。广度优先搜索过程中,每一个点至多只会被标记一次。
空间复杂度:O(n×m),其中 n 和 m 分别为矩阵的行数和列数。主要为广度优先搜索的队列的开销。