Leetcode 1572.矩阵对角线元素之和

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

示例 1：

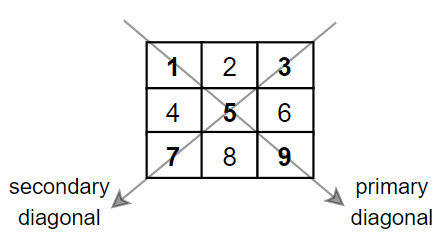
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

示例 2：

输入：mat = [[1,1,1,1],[1,1,1,1],[1,1,1,1],[1,1,1,1]]
输出：8

示例 3：

输入：mat = [[5]]
输出：5

提示：

n == mat.length == mat[i].length
1 <= n <= 100
1 <= mat[i][j] <= 100

通过次数

63.3K

提交次数

75.9K

通过率

83.3%

一、信息

1.给一个正方型矩阵mat

2.返回矩阵对角线元素的和

二、分析

条件1和条件2：告诉我此次的目的

问题1：该如何求和呢

根据我的思考步骤

第一步观察在矩阵中对角线元素的下标特征

通过观察我发现主对角线上数组元素的下标都满足i=j

副对角线都满足（n-1，0）（0，n-1）即关于主对角线对称，我觉得我该回去修一下线性代数了。

第二步我们通过for循环实现累加，if选择语句结构来筛选。

问题出现1：对了题目并没有说矩阵是几×几的矩阵所以还得测算矩阵的大小

问题出现该如何测算矩阵的大小

已知测算矩阵长度的是length函数。

答案：

Leetcode答案：

int n = mat.size(), sum = 0;

问题出现2：根据题目我们不难发现不仅我们要计算该二维数组的大小还要开辟动态的空间，这在C++该怎么办呢？

很简答其实用vector即可，如果不记得可以看文章（知识不足的地方）

不知道陷入了停滞

我的答案：

首先我们可以分析这个问题如下：

1. **思考过程**：
- 我们需要计算主对角线和副对角线上的元素和。主对角线上的元素位置是`mat[i][i]`，副对角线上的元素位置是`mat[i][n-1-i]`。
- 如果矩阵的尺寸是奇数，则中心元素会被计算两次，我们需要减去一次。

2. **分析过程**：
- 我们可以通过一个循环从 0 到 n-1 来遍历所有的行（或列），然后计算对角线元素的和。
- 如果 n 是奇数，我们减去一次`mat[n/2][n/2]`。

现在我们可以将这个逻辑实现为 C、C++ 和 Java 程序：

### C 语言实现

#include <stdio.h>int diagonalSum(int** mat, int matSize, int* matColSize){int sum = 0;for(int i = 0; i < matSize; i++){sum += mat[i][i] + mat[i][matSize - 1 - i];}if(matSize % 2 == 1){sum -= mat[matSize / 2][matSize / 2];}return sum;
}int main() {int mat1[3][3] = {{1,2,3}, {4,5,6}, {7,8,9}};int* mat1_ptr[3] = {mat1[0], mat1[1], mat1[2]};printf("%d\n", diagonalSum(mat1_ptr, 3, NULL)); // Output: 25return 0;
}

### C++ 语言实现

#include <vector>
#include <iostream>int diagonalSum(std::vector<std::vector<int>>& mat) {int sum = 0;int n = mat.size();for(int i = 0; i < n; i++) {sum += mat[i][i] + mat[i][n - 1 - i];}if(n % 2 == 1) {sum -= mat[n / 2][n / 2];}return sum;
}int main() {std::vector<std::vector<int>> mat1 = {{1,2,3}, {4,5,6}, {7,8,9}};std::cout << diagonalSum(mat1) << std::endl; // Output: 25return 0;
}

### Java 语言实现

public class Main {public static int diagonalSum(int[][] mat) {int sum = 0;int n = mat.length;for(int i = 0; i < n; i++) {sum += mat[i][i] + mat[i][n - 1 - i];}if(n % 2 == 1) {sum -= mat[n / 2][n / 2];}return sum;}public static void main(String[] args) {int[][] mat1 = {{1,2,3}, {4,5,6}, {7,8,9}};System.out.println(diagonalSum(mat1)); // Output: 25}
}

每种语言的实现都遵循了我们的原始分析和设计，结合了相应语言的特性和语法来实现目标功能。

Leetcode题解：

方法一：遍历矩阵
思路与算法

我们知道矩阵中某个位置 (i,j)(i,j)(i,j) 处于对角线上，则一定满足下列条件之一：

i=ji = ji=j；
i+j=n−1i + j = n - 1i+j=n−1；
根据上述结论，我们可以遍历整个矩阵，如果当前坐标 (i,j)(i, j)(i,j) 满足 i=ji = ji=j 或者 i+j=n−1i + j = n - 1i+j=n−1 则表示该位置一定在对角线上，则把当前的数字加入到答案之中。

class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;}
};

C：

int diagonalSum(int** mat, int matSize, int* matColSize) {int n = matSize, sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;
}

JAVA：

class Solution {public int diagonalSum(int[][] mat) {int n = mat.length, sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;}
}

方法二：枚举对角线元素
思路与算法

逐行遍历，记当前的行号为 iii，则当前行中处于对角线的元素为：坐标 (i,i)(i, i)(i,i) 和坐标 (i,n−i−1)(i, n - i - 1)(i,n−i−1)，因此我们把 (i,i)(i, i)(i,i) 与 (i,n−i−1)(i, n - i - 1)(i,n−i−1) 处的数字加入到答案中。如果 nnn 是奇数的话，则主对角线与副对角线存在交点 (⌊n2⌋,⌊n2⌋)(\lfloor \dfrac{n}{2} \rfloor,\lfloor \dfrac{n}{2} \rfloor)(⌊
2
n

⌋,⌊
2
n

⌋)，该点会被计算两次。所以当 nnn 为奇数的时候，需要减掉交点处的值。

C++：

class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0, mid = n / 2;for (int i = 0; i < n; ++i) {sum += mat[i][i] + mat[i][n - 1 - i];}return sum - mat[mid][mid] * (n & 1);}
};