目录
- 介绍
- 在TensorFlow中的应用
- 实战案例
- 最后
一、介绍
DenseNet(Densely Connected Convolutional Networks)是一种卷积神经网络(CNN)架构,2017年由Gao Huang等人提出。该网络的核心思想是密集连接,即每一层都接收其前面所有层的输出作为输入。DenseNet121是该家族中的一个特定模型,其中121表示网络的总层数。
DenseNet121的主要特点如下:
- 密集连接(Dense Connection):在一个Dense Block内,第 i 层的输入不仅仅是第 i−1 层的输出,还包括第 i−2 层、第 i−3 层等所有之前层的输出。这种密集连接方式促进了特征的重用。
- 参数效率:由于特征在网络中得以重复使用,DenseNet相较于其他深度网络模型(如VGG或ResNet)通常需要更少的参数来达到相同(或更好)的性能。
- 特征复用与强化:密集连接方式也促进了梯度的反向传播,使得网络更容易训练。同时,低层特征能被直接传播到输出层,因此被更好地强化和利用。
- 过拟合抑制:由于有更少的参数和更好的参数复用,DenseNet很适合用于数据集较小的场合,能在一定程度上抑制过拟合。
- 增加网络深度:由于密集连接具有利于梯度反向传播的特性,DenseNet允许构建非常深的网络。
- 计算效率:虽然有很多连接,但由于各层之间传递的是特征图(而不是参数或梯度),因此在计算和内存效率方面表现得相对较好。
- 易于修改和适应:DenseNet架构很容易进行各种修改,以适应不同的任务和应用需求。
DenseNet121在很多计算机视觉任务中都表现出色,例如图像分类、目标检测和语义分割等。因其出色的性能和高效的参数使用,DenseNet121常被用作多种视觉应用的基础模型。以下DeseNet算法与ResNet算法的区别。
| 特性/算法 | DenseNet | ResNet |
|---|---|---|
| 连接方式 | 每一层都与其前面的所有层密集连接 | 每一层仅与其前一层进行残差连接 |
| 参数效率 | 更高,由于特征复用 | 相对较低 |
| 特征复用 | 高度的特征复用,所有前面层的输出都用作每一层的输入 | 仅前一层的输出被用于下一层 |
| 梯度流动 | 由于密集连接,梯度流动更容易 | 通过残差连接改善梯度流动,但相对于DenseNet可能较弱 |
| 过拟合抑制 | 更强,尤其在数据集小的情况下 | 相对较弱 |
| 计算复杂度 | 一般来说更低,尽管有更多的连接 | 一般来说更高,尤其是在深层网络中 |
| 网络深度 | 可以更深,且更容易训练 | 可以很深,但通常需要更仔细的设计 |
| 可适应性 | 架构灵活,易于修改 | 相对灵活,但大多数改动集中在残差块的设计 |
| 创新点 | 密集连接 | 残差连接 |
| 主要应用 | 图像分类、目标检测、语义分割等 | 图像分类、目标检测、人脸识别等 |
这两种网络架构都在多种计算机视觉任务中表现出色,但根据具体应用的需求和限制,你可能会选择其中一种作为基础模型。
二、在TensorFlow中的应用
在TensorFlow(特别是TensorFlow 2.x版本)中使用DenseNet121模型非常方便,因为该模型已经作为预训练模型的一部分集成在TensorFlow库中。以下是一些常见用法的示例。
导入库和模型
首先,确保您已经安装了TensorFlow库。然后,导入所需的库和模型。
import tensorflow as tf
from tensorflow.keras.applications import DenseNet121
实例化模型
您可以通过以下方式实例化一个DenseNet121模型:
# 预训练权重和全连接层
model = DenseNet121(weights='imagenet', include_top=True)# 预训练权重但无全连接层(用于特征提取)
model = DenseNet121(weights='imagenet', include_top=False)
数据预处理
DenseNet121需要特定格式的输入数据。通常,您需要将输入图像缩放到224x224像素,并进行一些额外的预处理。
from tensorflow.keras.preprocessing import image
from tensorflow.keras.applications.densenet import preprocess_input
import numpy as npimg_path = 'your_image_path.jpg'
img = image.load_img(img_path, target_size=(224, 224))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
模型预测
使用预处理过的图像进行预测:
preds = model.predict(x)
三、实战案例
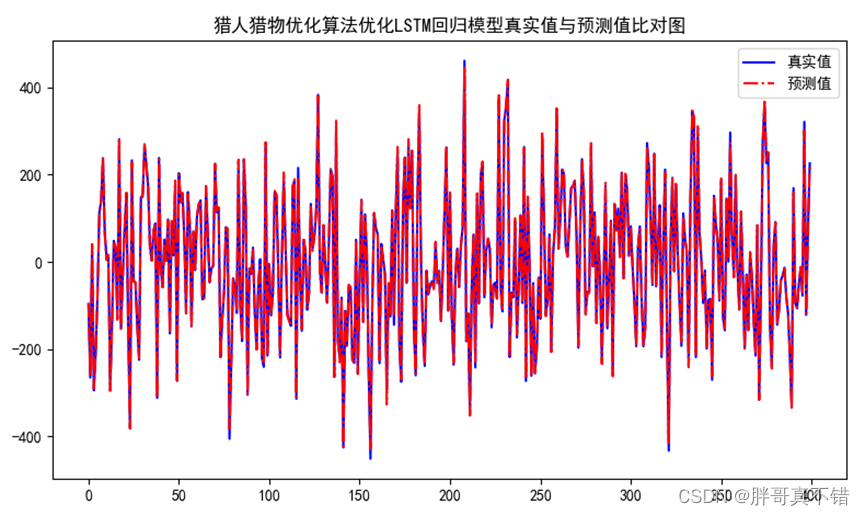
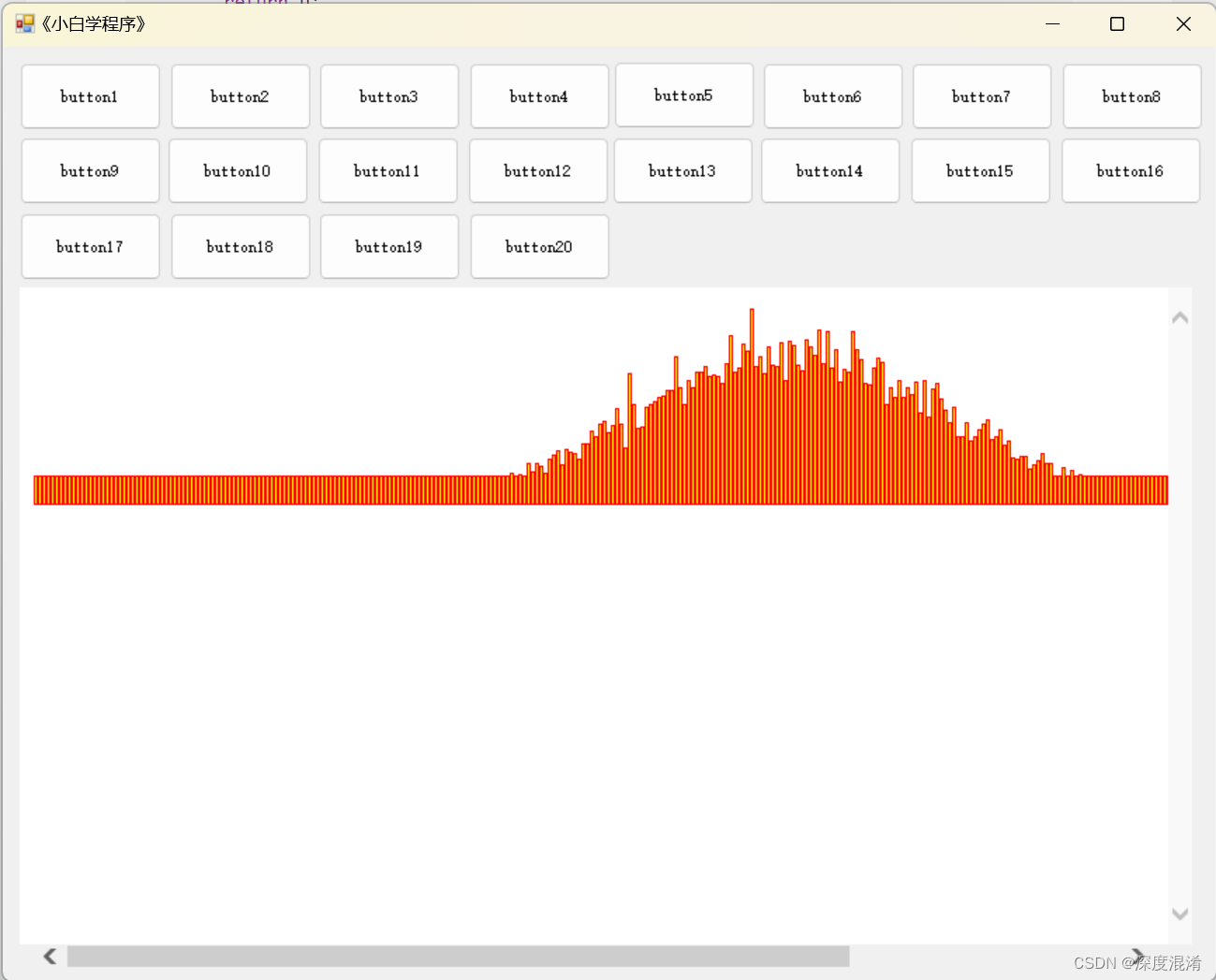
如下图所示,通过对几种常见的水果数据集进行训练,最后得到模型。下面是其经过25轮迭代训练的训练过程图、ACC曲线图、LOSS曲线图、可视化界面等
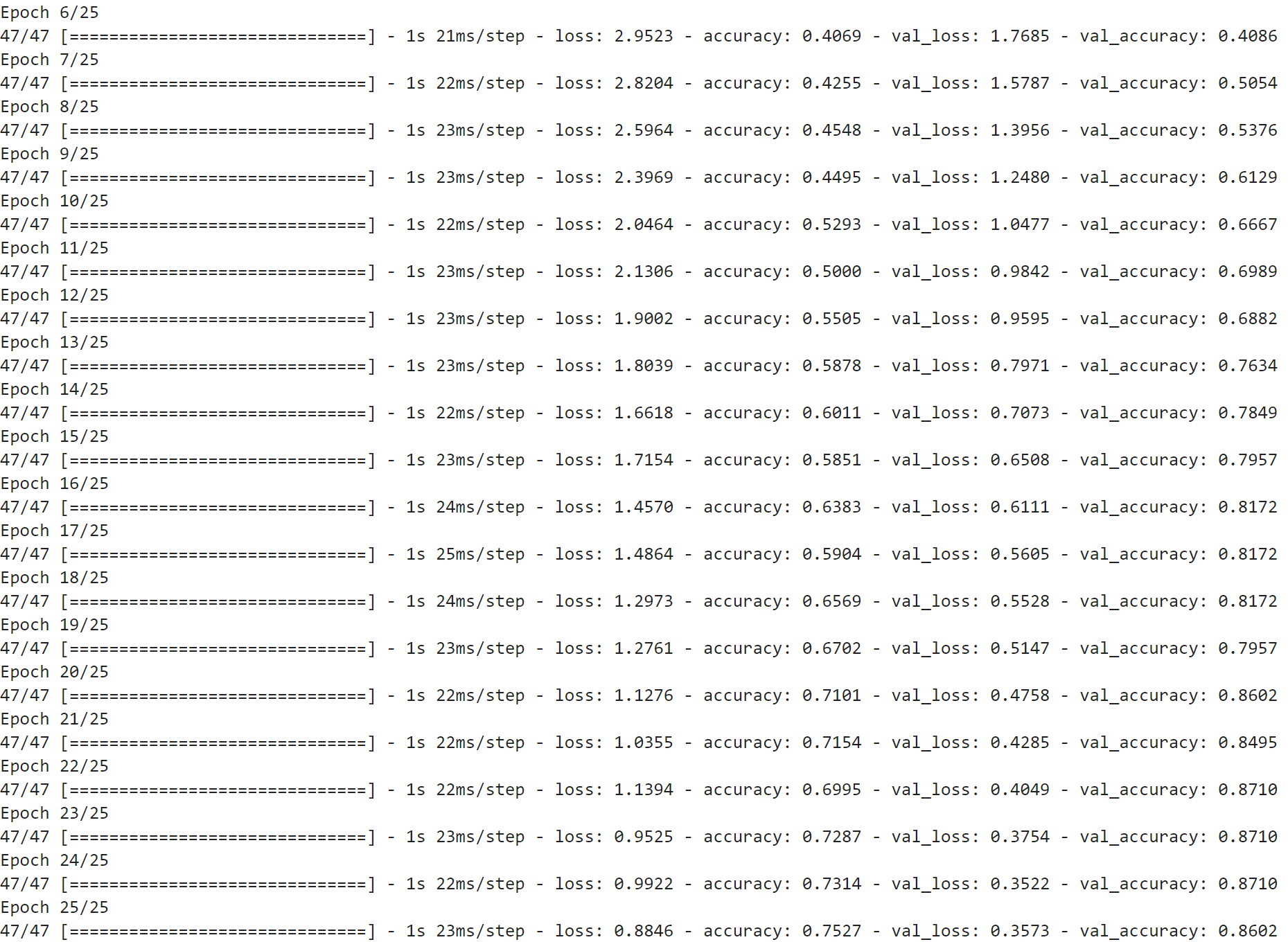
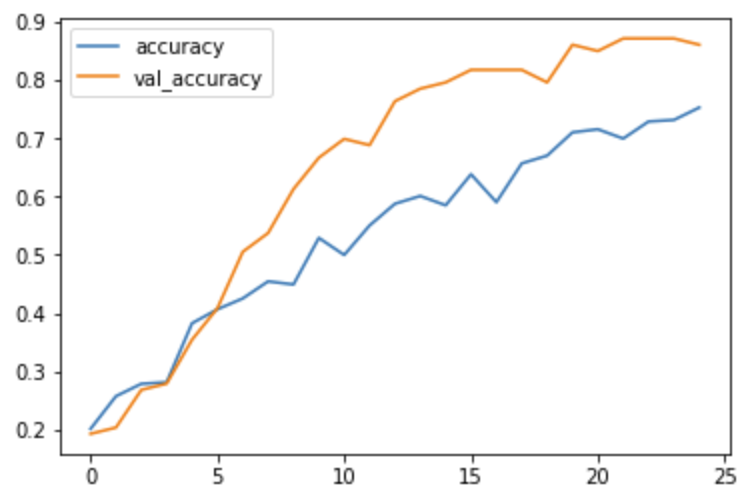
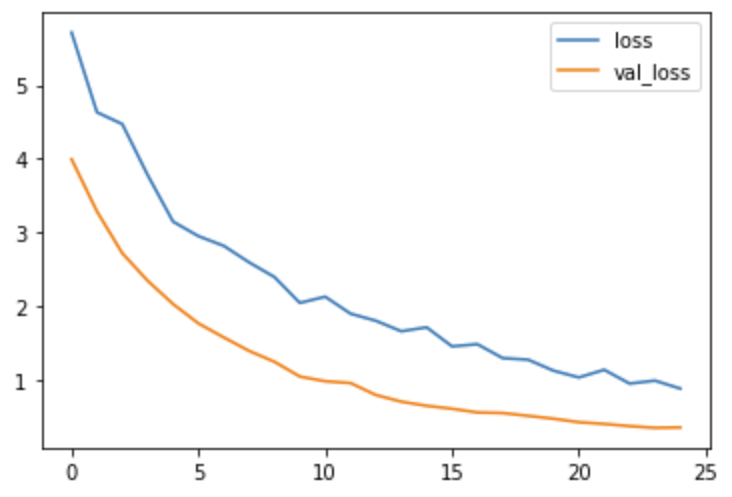
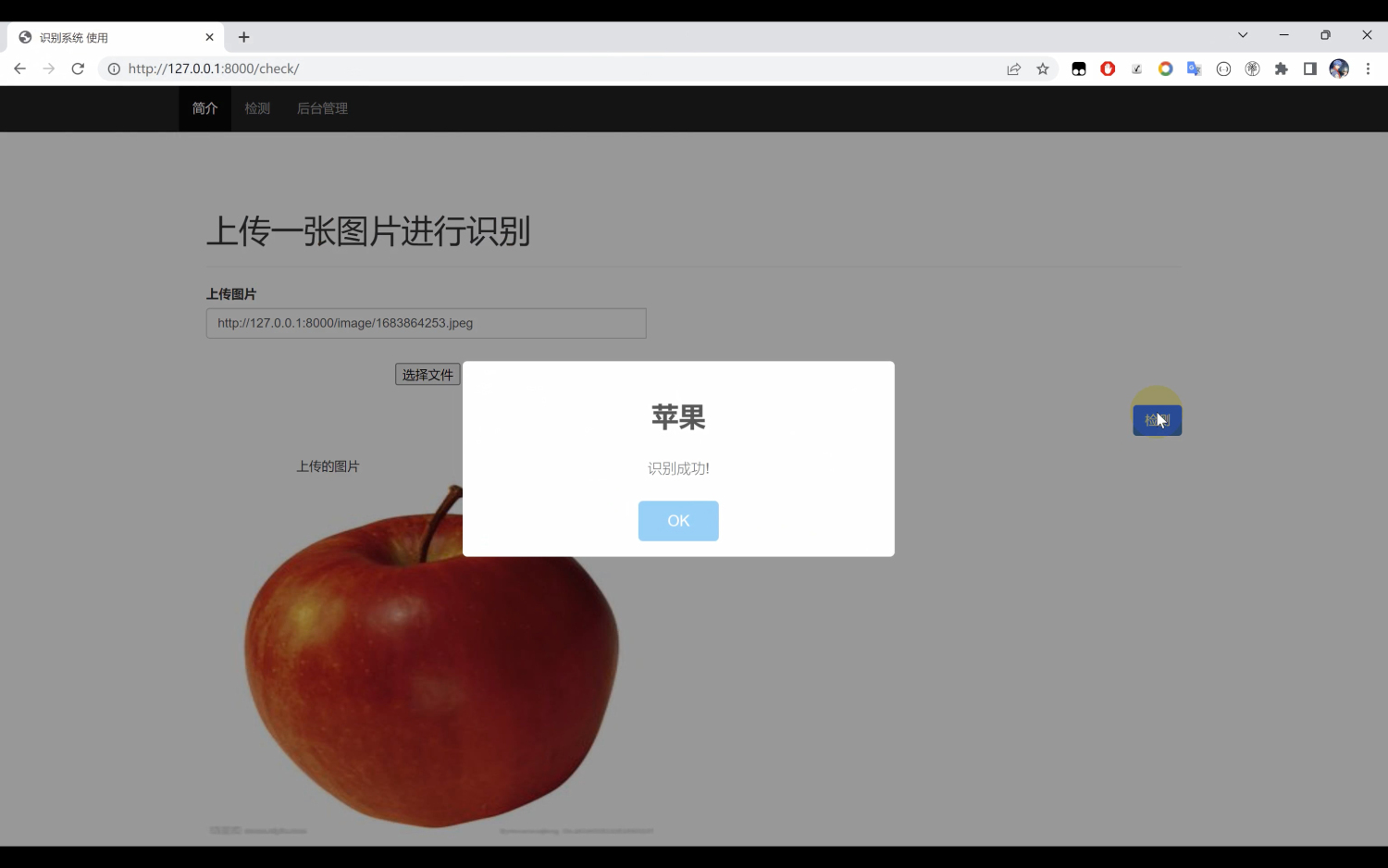
四、最后
大家可以尝试通过DenseNet121算法训练自己的数据集,然后封装成可视化界面部署等。由于研发投入项目付非提供(提供包括数据集、训练预测代码、训练好的模型、WEB网页端界面、包远程安装调试部署)。如需要请或类似项目订制开发请访问:https://www.yuque.com/ziwu/yygu3z/sr43e6q0wormmfpv