目录
一.理论知识
1.拟合与插值的区别
2.几何意义
3.误差分析
二.操作实现
1.数据准备
2.使用cftool——拟合工具箱
三.函数拟合典例
四.代码扩展
一.理论知识
1.拟合与插值的区别
通俗的说,插值的本质是根据现有离散点的信息创建出更多的离散点,从而不断提高精度;而拟合则不需要找到更多的点,目标在于根据已知的点构造出一条函数,使得每点上的误差尽可能地低——即曲线拟合的最好(最小化损失函数)。

2.几何意义
本质来说,就是尽可能找到——能经过当前全部点且误差最小的曲线。

理论部分这里不细说,涉及到最小二乘法,大家自行查资料~
3.误差分析

二.操作实现
1.数据准备
| x | 4.2 | 5.9 | 2.7 | 3.8 | 3.8 | 5.6 | 6.9 |
| y | 8.4 | 11.7 | 4.2 | 6.1 | 7.9 | 10.2 | 13.2 |
| x | 3.5 | 3.6 | 2.9 | 4.2 | 6.1 | 5.5 | 6.6 |
| y | 6.6 | 6 | 4.6 | 8.4 | 12 | 10.3 | 13.3 |
2.使用cftool——拟合工具箱
如上图,在APP菜单栏中找到“Curve Fitting”打开工具箱,或者在命令行输入:
cftool
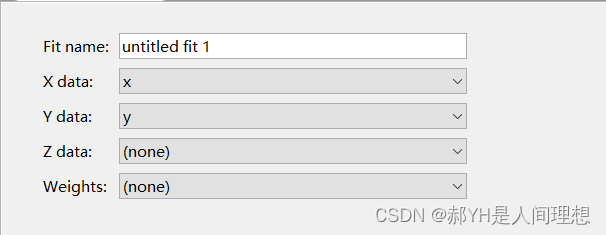
在工具箱页面的左上角,选择x与y对应的变量。
然后右下角就会出现函数图像,这是未拟合前的默认形态。
然后即可选择拟合方式,通常情况下多项式拟合即可得到不错的效果。
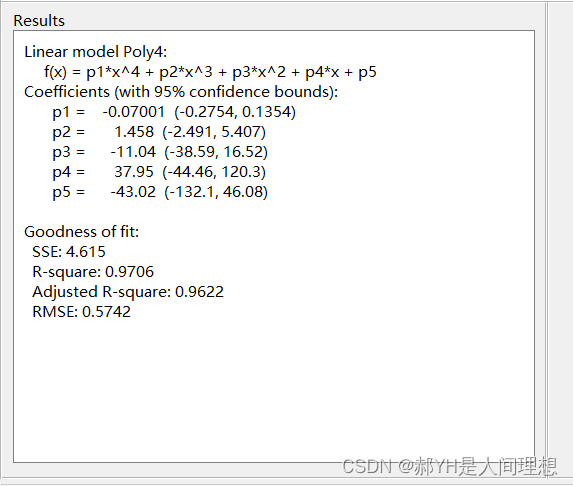
如上图,即为4次多项式拟合的效果。
如上是有关拟合误差的一些数据,需要重点关注的是:
- R值——拟合优度:当R值大于0.9或0.95时,即可认为拟合出来的函数可信度很高。
- 另外SSE等有关残差的参数也可以注意一下
左下角给出了一些拟合结果的内容,如上图可知:
y=-0.07001*x^4+1.458*x^3-11.04*x^2+37.95*x-43.02,即为本次拟合出的函数方程!
三.函数拟合典例
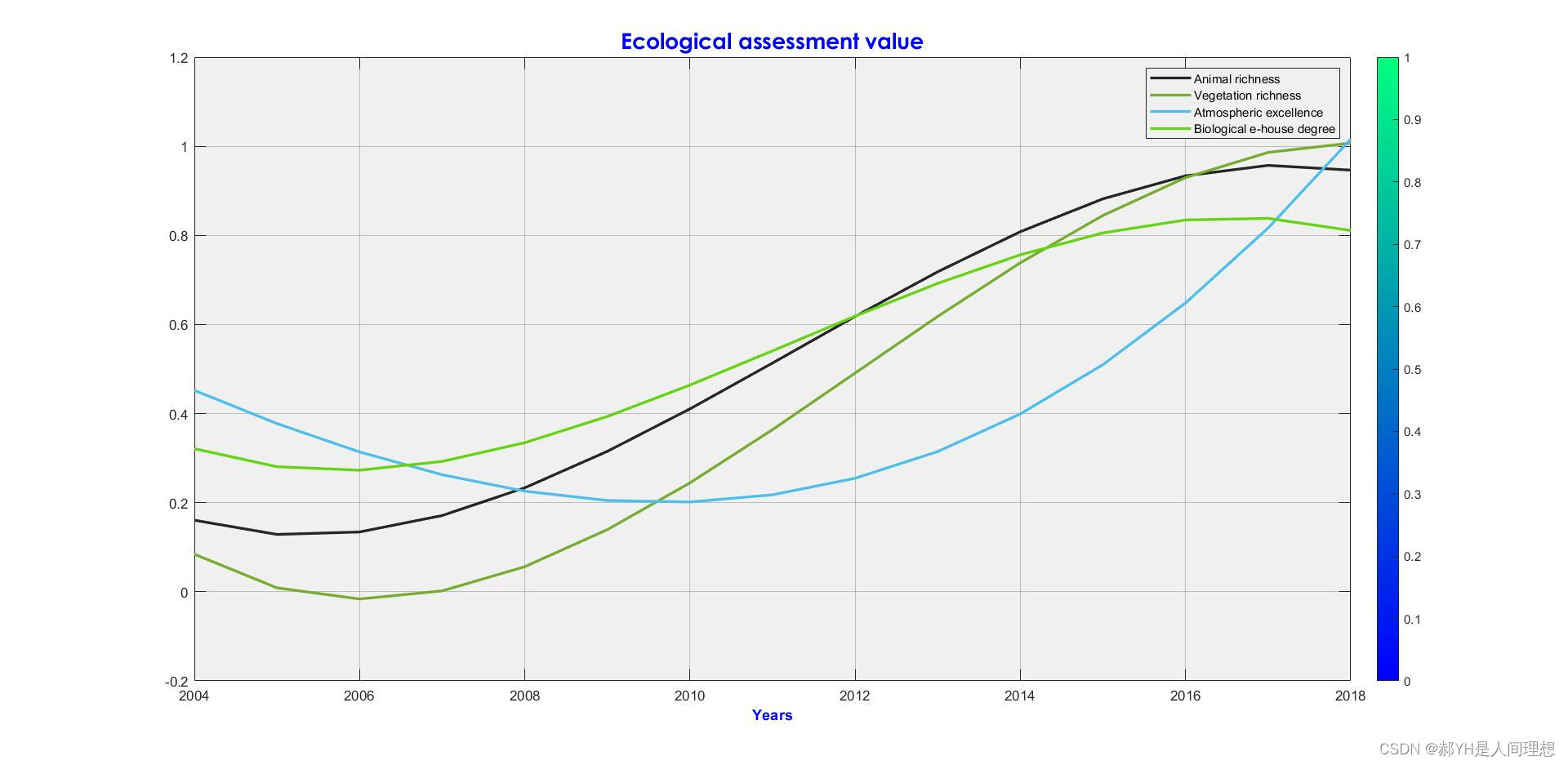
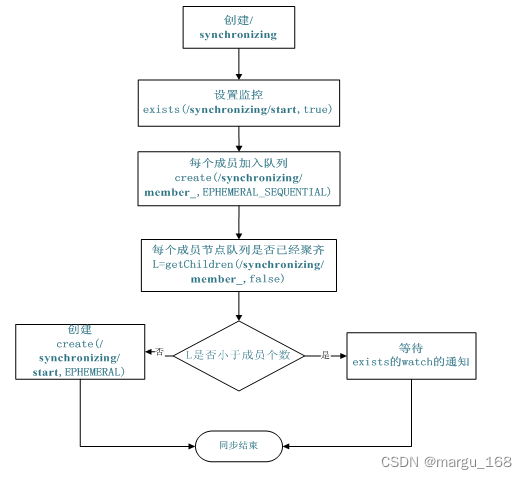
上图是2021年亚太数学建模中绘制的图片,根据有限数据量进行拟合得出具有函数性质的关系曲线
代码如下:
Time=[2004,2005,2006,2007,2008,2009,2010,2011,2012,2013,2014,2015,2016,2017,2018];
I1=[0.182948847,0.211434303,0,0.030892678,0.279638917,0.469635573,0.493306586,0.538642594,0.546666667,0.487288532,0.955466399,0.927382146,0.91334002,0.934603811,0.960280843];
I2=[0.022145329,0.034602076,0.033910035,0.028373702,0.044982699,0.195555556,0.277216455,0.342268358,0.349880815,0.364413687,0.919031142,0.990311419,1,0.948096886,0.948096886];
I3=[0.521140071,0.392131831,0.174670582,0.220460164,0.162032973,0.340698155,0.222348372,0.327533528,0.244249827,0.359156053,0.245644824,0.454187732,0.646707562,0.905064612,1];
I4=[0.36938131,0.374916005,0.117566088,0.148750878,0.372001753,0.388274379,0.51190998,0.705307237,0.695969953,0.706219511,0.591608401,0.759083664,0.819291342,0.822706134,0.874415287];
figure;
%% Create a canvas
a=polyfit(Time,I1,3);
plot(Time,I1,'.',Time,polyval(a,Time));%% Lock the current canvas,renders four function images on a single graph
hold on
b=polyfit(Time,I2,3);
plot(Time,I2,'.',Time,polyval(b,Time));
hold on
c=polyfit(Time,I3,3);
plot(Time,I3,'.',Time,polyval(c,Time));
hold on
d=polyfit(Time,I4,3);
plot(Time,I4,'.',Time,polyval(d,Time));
hold off
%% The command drawing part is finished, and the subsequent design is completed by graphic editing tools
%% FLG files will appear in the support material四.代码扩展
1.计算误差
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST2.产生随机数的一些操作:
% (1)randi : 产生均匀分布的随机整数(i = int)
%产生一个1至10之间的随机整数矩阵,大小为2x5;
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵,大小为1x10;
s2 = randi([-5,5],1,10)% (2) rand: 产生0至1之间均匀分布的随机数
%产生一个0至1之间的随机矩阵,大小为1x5;
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵,大小为1x5; % a + (b-a) * rand(1,5); 如:a,b = 2,5
s4= 2 + (5-2) * rand(1,5)% (3)normrnd:产生正态分布的随机数
%产生一个均值为0,标准差(方差开根号)为2的正态分布的随机矩阵,大小为3x4;
s5 = normrnd(0,2,3,4)% (4)roundn—任意位置四舍五入
% 0个位 1十位 2百位 -1小数点后一位
a = 3.1415
roundn(a,-2) % ans = 3.1400
roundn(a,2) % ans = 0
a =31415
roundn(a,2) % ans = 31400
roundn(5.5,0) %6
roundn(5.5,1) %10写在最后:对于数学建模竞赛来说,拟合并不是一种很高端的计算手段——仅在需要明确的函数方程时才建议使用。对于预测类的问题,建议使用回归、灰色预测、BP神经网络等模型。