红黑树

搜索二叉树
搜索二叉树的模拟实现
- 平衡搜索二叉树(AVL Tree)
- 平衡搜索二叉树的模拟实现
- - 红黑树(Red Black Tree)
  - - - 红黑树的模拟实现
    - 红黑树的应用(Map 和 Set)
    - - Map和Set的封装

搜索二叉树

搜索二叉树的概念：二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

简单来说，搜索二叉树的一个原则：如果左右树，根不为空，左树永远比根小，右树永远比根大
这个原则可运用到搜索二叉树的每个节点

用一张图来了解搜索二叉树：
在这里插入图片描述

二叉搜索树的优点：
查找效率：如果现在要在数组中查找一个数字是否存在，我们只能去遍历数组，但是如果在搜索二叉树中查找，从根节点开始判断，要么查找的数比根小，要么比根大，要么和根相等，如果要找的数在左边，那么右树可以全部排除，如果在右边，那么左边的数可以全部排除，以此往复下去，每次都可以将一半的数据排除，所以查找效率大大提高

二叉搜索树的缺点：
极端情况：还是在二叉搜索树中查找一个数字，但是这个时候出现了一个极端情况
上图：
在这里插入图片描述

这颗树符合搜索二叉树的原则吗？
答案是当然，如果左右树不为空，左树永远比根小，右树永远比根大，很显然这颗树就是搜索二叉树
那么再来看一张图
在这里插入图片描述

这颗树是搜索二叉树吗？
我就不多说了

如果在以上两种情况下，树的节点向左或者向右呈现线型结构，这个时候再去查询一个数据，假设这个数据在最下面，比如上图中的 16 ，那搜索二叉树和数组有什么区别？所以如果碰到这种极端情况，搜素二叉树的优势就全没了

但是在一般的情况下，搜索二叉树的查找效率和远远优于数组的

搜索二叉树的模拟实现

直接上代码：
先来看一下搜索二叉树的整体框架

#pragma once
#include<iostream>using namespace std;//自定义命名空间
namespace ys
{//定义搜索二叉树的节点//使用模板来定义数据类型template<class T>struct TreeNode{T _val;//数据TreeNode* _left;//左树TreeNode* _right;//右树//构造函数初始化TreeNode(T data):_val(data),_left(nullptr),_right(nullptr){}};//定义搜索二叉树类//使用模板接受数据类型template<class T>class Tree{//对树的结构体进行重命名，方便后续操作typedef TreeNode node;public://插入bool insert(){}//删除bool erase(){}//查询bool find(){}//打印整颗树void Printf(){}private:node* _root = nullptr;//根节点};
}

总共4个接口，我们来逐一攻破
先从查询（find）开始：
在搜索二叉树中查询一个数字是否存在，从根节点开始查找，如果等于根节点返回true，否则和根节点比较大小，比根小转到左树去查找，比根大转到右树去查找
代码：

//查询bool find(const T& data){node* cur = _root;while (cur){//找到了if (data == cur->_val) return true;if (data < cur->_val) cur = cur->_left;//比根小，转到左树else cur = cur->_right;//比根大，转到右树}return false;}

插入(insert)：和查询的逻辑大差不差，首先还是比较，要插入的数字比根小，转到左树寻找要插入的位置，比根大，转到右树寻找要插入的位置

//插入bool insert(const T& data){//如果根为空，说明是空树，直接插入根即可if (_root == nullptr){_root = new node(data);return true;}else{//首先查询树中是否有data，如果有直接返回falseif (find(data)) return false;//如果没有再进行插入node* cur = _root;node* prev = nullptr;while (cur){//如果data小于根，在左树寻找插入位置if (data < cur->_val){prev = cur;cur = cur->_left;}//如果data大于根，在右树寻找插入位置else{prev = cur;cur = cur->_right;}}//循环结束，说明已经找到了插入的位置//插入到prev下面的两颗子树//判断插入prev左边还是右边if (data > prev->_val)prev->_right = new node(data);elseprev->_left = new node(data);return true;}}

最关键的来了，删除(erase)
删除的步骤：
1，找到要删除的节点(cur)的父树(prev)

2，判断要删除的节点是否有左右树
(1)如果只有左树，将cur的左树连接到prev
(2)如果只有右树，将cur的右树连接到prev

3，如果左右树都有
(1)将左树的最大节点和要删除的节点进行替换
(2)将右树的最小节点和要删除的节点进行替换

//删除bool erase(const T& data){//树为空，返回falseif (_root == nullptr) return false;node* cur = _root;node* prev = nullptr;//记录父节点//找到要删除的节点while (cur){if (data < cur->_val){prev = cur;cur = cur->_left;}else if(data > cur->_val){prev = cur;cur = cur->_right;}//找到了要删除的节点//判断要删除的节点是否拥有左右树else{//如果cur的左树为空，直接将cur的右树和cur的父树连接if (cur->_left == nullptr){//判断cur是否为根节点if (cur == _root){//如果cur就是根节点，并且左树为空，直接将cur的第一个右树设为root_root = cur->_right;}else{if (prev->_left == cur) prev->_left = cur->_right;else prev->_right = cur->_right;}}//如果cur的右树为空，直接将cur的左树和cur的父树连接else if (cur->_right == nullptr){//判断cur是否为根节点if (cur == _root){//如果cur就是根节点，并且左树为空，直接将cur的第一个右树设为root_root = cur->_right;}else{if (prev->_right == cur) prev->_right = cur->_left;else prev->_left = cur->_left;}}//如果要删除的节点同时拥有左右树，有两种删除方法else{//1，使用左树的最大节点进行替换//2，使用右树的最小节点进行替换//这里我们采用第一种方法，使用左树的最大节点进行替换node* leftmax = cur->_left;node* pleftmax = nullptr;//找到左树的最大节点while (leftmax){pleftmax = leftmax;leftmax = leftmax->_right;}//如果左树的最大节点有左树//将最大节点的左树连接到他的父树if (leftmax->_left){pleftmax->_right = leftmax;}//将要删除节点的数据和左树最大节点继续交换cur->_val = leftmax->_val;//释放左树最大节点delete leftmax;leftmax = nullptr;}return true;}}return false;}

中序遍历：
这个就不多说了，直接上代码

void _printf(node* root){if (root == nullptr) return;_printf(root->_left);cout << root->_val << " ";_printf(root->_right);}//中序遍历打印整颗树void Printf(){if (_root == nullptr) cout << "空树" << endl;_printf(_root);}

整体代码：

#pragma once
#include<iostream>using namespace std;//自定义命名空间
namespace ys
{//定义搜索二叉树的节点//使用模板来定义数据类型template<class T>struct TreeNode{T _val;//数据TreeNode* _left;//左树TreeNode* _right;//右树//构造函数初始化TreeNode(T data):_val(data),_left(nullptr),_right(nullptr){}};//定义搜索二叉树类//使用模板接受数据类型template<class T>class Tree{typedef TreeNode<T> node;public://插入bool insert(const T& data){//如果根为空，说明是空树，直接插入根即可if (_root == nullptr){_root = new node(data);return true;}else{//首先查询树中是否有data，如果有直接返回falseif (find(data)) return false;//如果没有再进行插入node* cur = _root;node* prev = nullptr;while (cur){//如果data小于根，在左树寻找插入位置if (data < cur->_val){prev = cur;cur = cur->_left;}//如果data大于根，在右树寻找插入位置else{prev = cur;cur = cur->_right;}}//循环结束，说明已经找到了插入的位置//插入到prev下面的两颗子树//判断插入prev左边还是右边if (data > prev->_val)prev->_right = new node(data);elseprev->_left = new node(data);return true;}}//删除bool erase(const T& data){//树为空，返回falseif (_root == nullptr) return false;node* cur = _root;node* prev = nullptr;//记录父节点//找到要删除的节点while (cur){if (data < cur->_val){prev = cur;cur = cur->_left;}else if(data > cur->_val){prev = cur;cur = cur->_right;}//找到了要删除的节点//判断要删除的节点是否拥有左右树else{//如果cur的左树为空，直接将cur的右树和cur的父树连接if (cur->_left == nullptr){//判断cur是否为根节点if (cur == _root){//如果cur就是根节点，并且左树为空，直接将cur的第一个右树设为root_root = cur->_right;}else{if (prev->_left == cur) prev->_left = cur->_right;else prev->_right = cur->_right;}}//如果cur的右树为空，直接将cur的左树和cur的父树连接else if (cur->_right == nullptr){//判断cur是否为根节点if (cur == _root){//如果cur就是根节点，并且左树为空，直接将cur的第一个右树设为root_root = cur->_right;}else{if (prev->_right == cur) prev->_right = cur->_left;else prev->_left = cur->_left;}}//如果要删除的节点同时拥有左右树，有两种删除方法else{//1，使用左树的最大节点进行替换//2，使用右树的最小节点进行替换//这里我们采用第一种方法，使用左树的最大节点进行替换node* leftmax = cur->_left;node* pleftmax = nullptr;//找到左树的最大节点while (leftmax){pleftmax = leftmax;leftmax = leftmax->_right;}//如果左树的最大节点有左树//将最大节点的左树连接到他的父树if (leftmax->_left){pleftmax->_right = leftmax;}//将要删除节点的数据和左树最大节点继续交换cur->_val = leftmax->_val;//释放左树最大节点delete leftmax;leftmax = nullptr;}return true;}}return false;}//查询bool find(const T& data){node* cur = _root;while (cur){//找到了if (data == cur->_val) return true;if (data < cur->_val) cur = cur->_left;//比根小，转到左树else cur = cur->_right;//比根大，转到右树}return false;}void _printf(node* root){if (root == nullptr) return;_printf(root->_left);cout << root->_val << " ";_printf(root->_right);}//中序遍历打印整颗树void Printf(){if (_root == nullptr) cout << "空树" << endl;_printf(_root);}private:node* _root = nullptr;//根节点};
}

测试用例：
插入：
在这里插入图片描述

查询：
在这里插入图片描述

删除：
在这里插入图片描述

平衡搜索二叉树(AVL Tree)

搜索二叉树有两个极端情况
1，当所有的节点都只有左树，那么整颗树就会呈现出向左的一条线性结构
在这里插入图片描述

2，当所有的节点都只有右树，那么整颗树就会呈现出向右的一条线性结构
在这里插入图片描述
AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写，他们两个提出的平衡二叉树的概念，为了纪念他们，将平衡二叉树称为 AVL树。
当搜索二叉树出现这两种情况的时候，搜索二叉树的优势就全没有了，所以为了避免这种情况出现，伟大的早期程序员设计出了平衡搜索二叉树(AVL树)

AVL树的概念：
AVL树本质是就是一棵搜索二叉树，【但是】，为了不让树呈现出一边倒的现象，AVL树的设计者又给加了两个原则：
1，它是一棵空树或它的左右两个子树的高度之差(简称平衡因子)不超过1，
2，左右两个子树也都是一棵平衡二叉树。

平衡因子：
一个没有左树和右树的节点平衡因子为0
如果插入一个左树，平衡因子减1
如果插入一个右树，平衡因子加1
不论是平衡因子减1或者加1，当前节点的父树的平衡因子也要跟随变动，依次类推
【注意】当平衡因子>= 2或者<= -2的时候，说明这颗树已经不平衡了，所以此时不要再向上调整父树平衡因子，而是在不平衡的节点做出处理

AVL树的旋转
1，左单旋
当一棵AVL树的右树高于左树的时候，将右树向左边旋转
在这里插入图片描述
旋转方式：1，将25连接到20的右树

2，将20练级到65的左树
在这里插入图片描述
旋转完成，树已经达成平衡状态

2，右单旋
当一个AVL树的左树高于右树，将左树向右旋转
在这里插入图片描述

1,将60连接到70的左树
在这里插入图片描述
2，将70连接到50的右树

旋转完成，树已经达成平衡状态

3，左右旋
新节点插入较高左子树的右侧—左右：先左单旋再右单旋
在这里插入图片描述
1，将2进行左旋

2，将5进行右旋

旋转完成，树已经达成平衡状态

4，右左旋
新节点插入较高右子树的左侧—右左：先右单旋再左单旋
在这里插入图片描述

先将5进行右旋
在这里插入图片描述
再将2进行左旋

平衡搜索二叉树的模拟实现

直接上代码：

#include<iostream>
#include<assert.h>
using namespace std;namespace avlt
{template<class K,class V>struct AvlNode{pair<K,V> _kv;//值AvlNode* _left;//左树AvlNode* _right;//右树AvlNode* _parent;//父树int _bf;//平衡因子AvlNode(const pair<K, V>& data ):_kv(data),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}};template<class K,class V>class AvlTree{typedef AvlNode<K,V> node;public://插入bool insert(const pair<K, V>& data){//判断根节点是否为空if (_root == nullptr){//如果根节点为空，直接插入根节点_root = new node(data);return true;}//查询树中是否已经存在要插入的数据if (find(data.first)){cout << data.first << "已存在" << endl;return false;}//首先找到要插入的节点node* cur = _root;node* parent = nullptr;while (cur){if (cur->_kv.first > data.first){parent = cur;cur = cur->_left;}else {parent = cur;cur = cur->_right;}}//插入并连接cur = new node(data);if (parent->_kv.first > cur->_kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//向上更新平衡因子,直到检查到根节点while (parent){//更新平衡因子if (parent->_left == cur)parent->_bf--;elseparent->_bf++;//以parent为根节点的树是平衡的，但不是完全平衡，继续向上更新if (parent->_bf == 1 || parent->_bf == -1){//cur = cur->_parent;cur = parent;parent = parent->_parent;}//平衡因子为0，说明树是平衡的，不要再做调整，直接跳出循环else if (parent->_bf == 0){break;}//平衡因子不平衡else if(parent->_bf == 2 || parent->_bf == -2){//右树高，左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//左树高，右单旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左树的右树高,先左旋再右旋else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//右树的左树高，先右旋再左旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}elseassert(false);break;}elseassert(false);}return true;}private://旋转//左旋void RotateL(node* parent){node* subR = parent->_right;node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}parent->_bf = subR->_bf = 0;}//右旋void RotateR(node* parent){node* subL = parent->_left;node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}subL->_bf = parent->_bf = 0;}//左右旋void RotateLR(node* parent){node* subL = parent->_left;node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{cout << "左右旋" << endl;assert(false);}}//右左旋void RotateRL(node* parent){node* subR = parent->_right;node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{cout << "右左旋" << endl;assert(false);}}//查询bool find(const K& data){if (_root == nullptr) return false;node* cur = _root;while (cur){if (cur->_kv.first == data)return true;if (cur->_kv.first > data)cur = cur->_left;elsecur = cur->_right;}return false;}
public://中序遍历void _print(node* root){if (root == nullptr) return;_print(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_print(root->_right);}void print(){_print(_root);}private:node* _root = nullptr;//根结点};
}

来看一下效果;
在这里插入图片描述

我们多试几次：

红黑树(Red Black Tree)

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

红黑树的性质

每个结点不是红色就是黑色
根节点是黑色的
如果一个节点是红色的，则它的两个孩子结点是黑色的
对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

红黑树本身就是一棵AVL树，但是他比AVL树具有更高的效率

当红黑树不平衡的时候，他不能像AVL树那样只进行旋转，而是旋转加变色

假设现在有一个红黑树
cur为新插入的节点
在这里插入图片描述
此时新插入的cur违反了红黑树【如果一个节点是红色的，则它的两个孩子结点是黑色的】的规则
那么怎么解决这个问题呢？

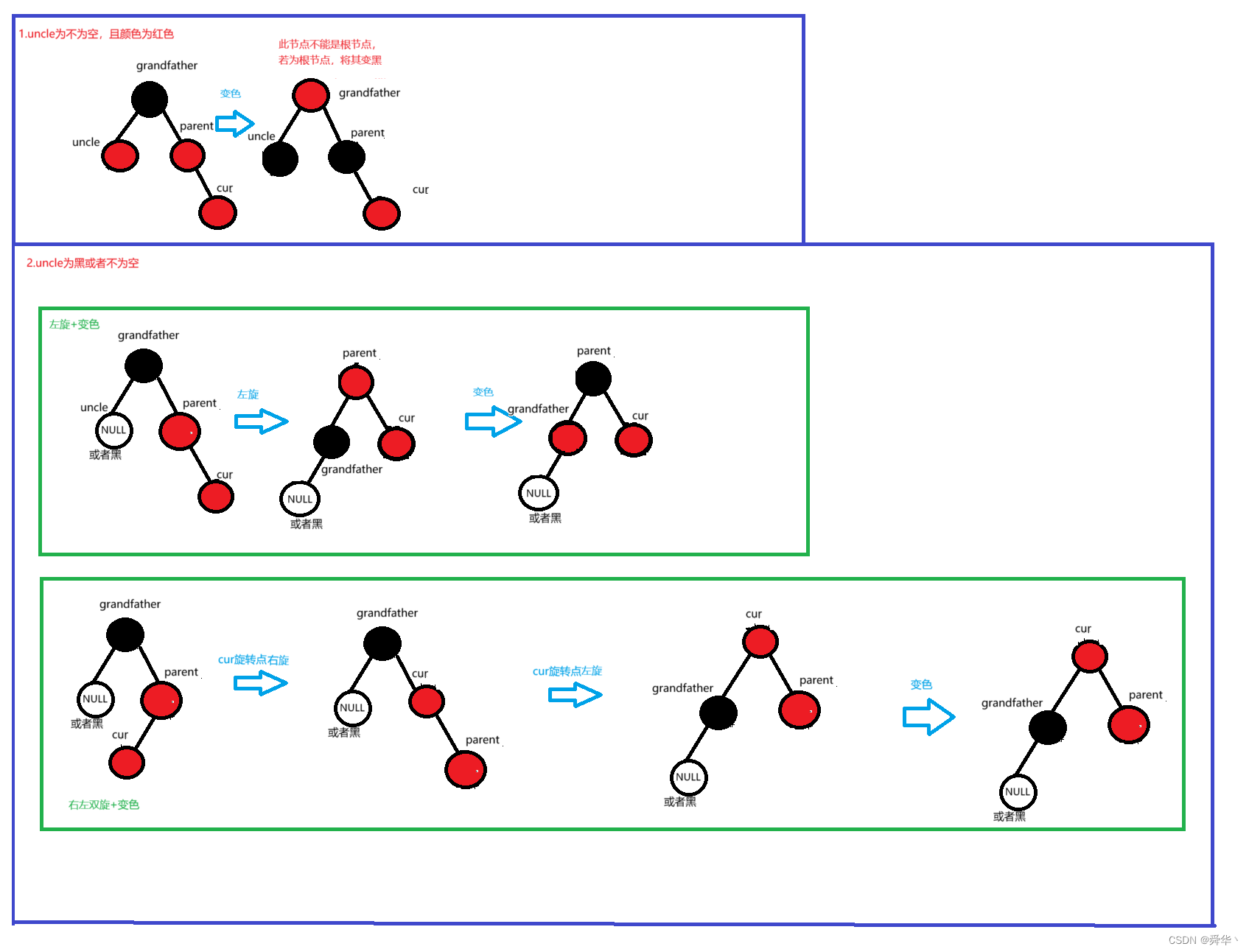
第一种情况，叔叔节点存在且为红色（只变色）

第一步，判断父树是否为黑色节点，如果是黑色节点，那就不用做处理，因为没有违反红黑树的规则

第二步，如果父树是红色节点，将父树变成黑色节点
在这里插入图片描述
第三步，如果叔叔节点存在，将叔叔节点（父树的兄弟节点）也变成黑色

第四步，将爷爷节点变成红色

第五步，将爷爷节点当做一个新插入的节点，继续向上更新变色

然后重复上面的4个步骤：
在这里插入图片描述
如果最后发现走到了根节点，必须将根节点变成黑色

第二种情况：旋转加变色
当插入的节点没有叔叔节点的时候
在这里插入图片描述
首先将爷爷节点进行右单旋

再将父节点变成黑色，爷爷节点变成红色

第三种情况：叔叔存在且为黑
在这里插入图片描述
首先cur是新增节点，但是一般情况下，叔叔节点颜色和父节点颜色是相同的，但是，当上面这种情况出现后，向上调整会变成：

由于向上调整变色，4被当做新增节点，此时4的叔叔节点是黑色，父节点是红色，这个时候就要采用双旋的方案来解决这个问题
1，将2左旋
在这里插入图片描述
2，对7进行右旋

最后进行变色
在这里插入图片描述

当然红黑树增加节点旋转变色的情况很多，但是上述几种方案基本概述了所有情况的原理，其他情况与之不同的就是旋转的方向不一样，原理都是一样的

红黑树的模拟实现

话不多说，直接上代码：

#pragma once
#include<iostream>using namespace std;namespace rb_tree
{//枚举定义节点颜色enum Colour{RED,BLACK};//红黑树节点template<class K,class V>struct RBTreeNode{pair<K, V> _kv;//数据RBTreeNode* _left;//左树RBTreeNode* _right;//右树RBTreeNode* _parent;//父树Colour _col;//节点颜色RBTreeNode(const pair<K, V>& data):_kv(data),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED)//节点颜色初始化为红色{}};template<class K,class V>class RBTree{typedef RBTreeNode<K,V> node;public://插入bool insert(const pair<K,V>& data){//如果根节点为空，插入根节点，并将颜色改为黑色if (_root == nullptr){_root = new node(data);_root->_col = BLACK;return true;}//找到可以插入的地方node* cur = _root;node* parent = nullptr;while (cur){if (cur->_kv.first > data.first){parent = cur;cur = cur->_left;}else if(cur->_kv.first < data.first){parent = cur;cur = cur->_right;}else return false;}//插入并连接cur = new node(data);if (parent->_kv.first > cur->_kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//如果父节点是黑色，插入的节点是红色，直接返回true，不需要做处理if (parent->_col == BLACK) return true;//如果父节点是红色，开始处理while (parent && parent->_col == RED){//找到祖父节点node* grandfather = parent->_parent;//找到叔叔节点if (grandfather->_left == parent){node* uncle = grandfather->_right;//如果叔叔节点不为空且是红色if (uncle && uncle->_col == RED){//将叔叔和父节点变黑uncle->_col = parent->_col = BLACK;//将祖父节点变红grandfather->_col = RED;//继续向上调整cur = grandfather;parent = cur->_parent;}//叔叔节点存在且为黑，或者叔叔节点不存在else{//第一种情况//     g//   p   u// cif (cur == parent->_left){//对p继续右旋RotateR(parent);//再进行变色parent->_col = BLACK;grandfather->_col = RED;}//第二种情况//    g//  p   u//    celse{//先左旋parentRotateL(parent);//再右旋grandfatherRotateR(grandfather);//变色grandfather->_col = RED;cur->_col = BLACK;}break;}}//如果parent是祖父节点的右边，叔叔节点就是祖父节点的左边else{//找到叔叔节点node* uncle = grandfather->_left;//如果叔叔节点存在且为红if (uncle && uncle->_col == RED){uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}//如果叔叔节点不存在或存在且为黑else{//第一种情况//      g//    u   p//          cif (cur == parent->_right){//首先对grandfather进行左单旋RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}//第二种情况//      g//   u     p//       celse{//首先对parent进行右单旋RotateR(parent);//再对grandfather进行左单旋RotateL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}}break;}}//不论什么情况下，根节点都必须是黑色的_root->_col = BLACK;return true;}//中序遍历void _print(node* root){if (root == nullptr) return;_print(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_print(root->_right);}void print(){_print(_root);}private://左单旋void RotateL(node* parent){node* SubR = parent->_right;node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL)SubRL->_parent = parent;node* pparent = parent->_parent;parent->_parent = SubR;SubR->_left = parent;if (pparent){if (pparent->_left == parent)pparent->_left = SubR;elsepparent->_right = SubR;SubR->_parent = pparent;}else{_root = SubR;SubR->_parent = nullptr;}}//右单旋void RotateR(node* parent){node* SubL = parent->_left;node* SubLR = SubL->_right;node* pparent = parent->_parent;parent->_left = SubLR;SubL->_right = parent;parent->_parent = SubL;if (SubLR)SubLR->_parent = parent;if (pparent){if (pparent->_left == parent)pparent->_left = SubL;elsepparent->_right = SubL;SubL->_parent = pparent;}else{_root = SubL;SubL->_parent = nullptr;}}private:node* _root = nullptr;//根节点};
}

测试一下：

#include"RBTree.h"
#include<set>
#include<map>
#include<utility>
#include<ctime>
using namespace std;void test1()
{srand(time(nullptr));rb_tree::RBTree<int, int> rb;for (int i = 0; i < 30; i++){rb.insert(make_pair(rand() % 100, rand() % 10));}rb.print();
}int main()
{test1();return 0;
}

在这里插入图片描述
再试几次

没毛病…

红黑树的应用(Map 和 Set)

Map和Set的基本使用

Map和Set的封装

看完Map和Set的基本使用，基于上面的红黑树代码我们来手写一个简单的Map和Set
主要功能有三个，插入，查询，迭代器

重点说一下迭代器和红黑树的模板参数设计：

STL的map和set是共用红黑树的代码的，也就是说，一张红黑树的代码，map可以直接封装，set也可以
在这里插入图片描述

我们来看上面我们写的红黑树代码：
在这里插入图片描述

在这里插入图片描述

我们设计的红黑树是key Value结构的，如果是用在map上，是合适的
但是set呢？set的key就是value，但往往set只有一个参数，而要使用红黑树至少得两个参数，那就不能使用这个红黑树了
在这里插入图片描述

怎么办？STL的设计者想出了一个非常棒的点子，修改红黑树的模板参数
在这里插入图片描述

在这里插入图片描述

set
在这里插入图片描述

map
在这里插入图片描述

我们来画图演示一下：
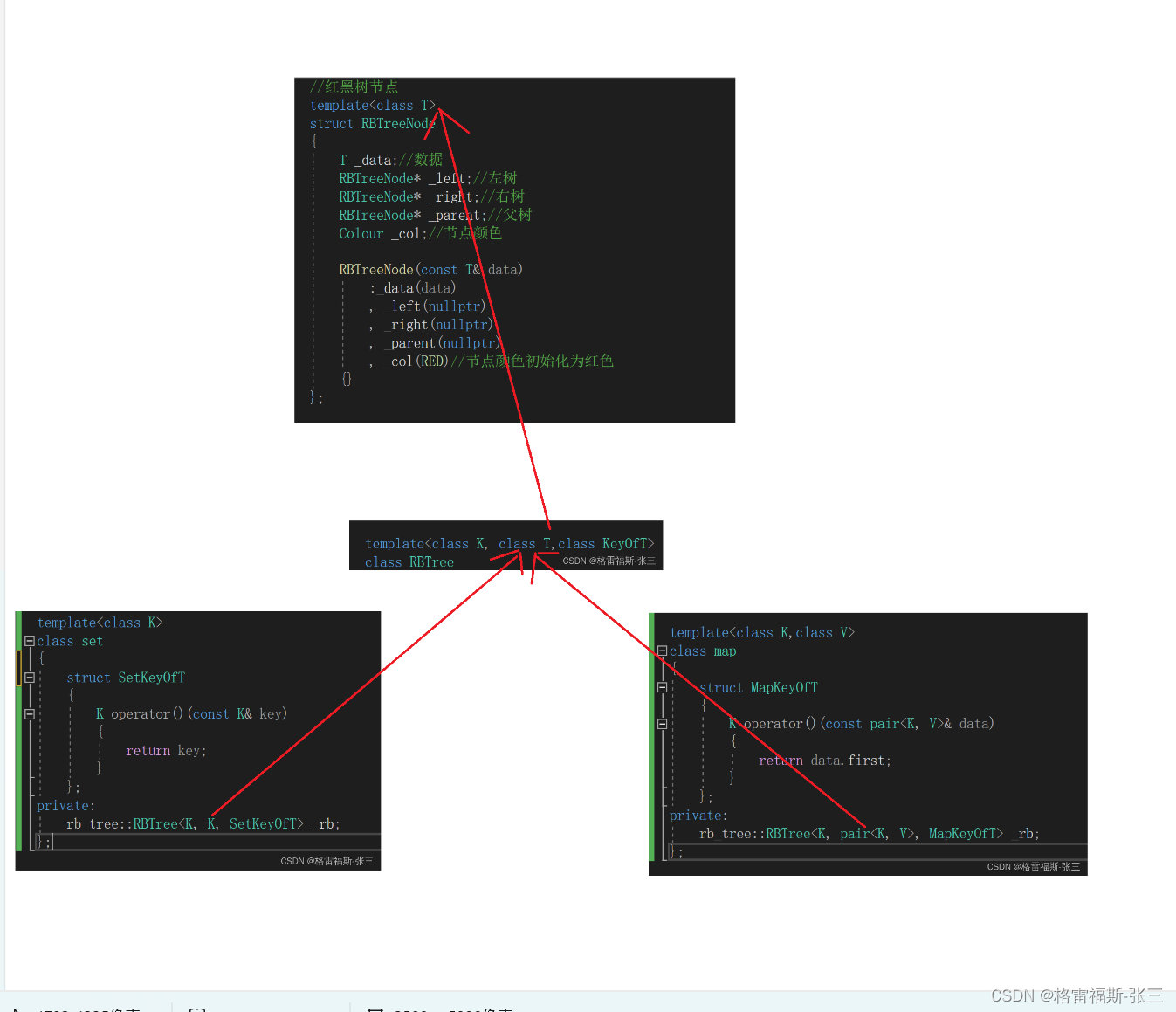
在这里插入图片描述
首先将红黑树的参数改成三个，第一个参数不重要，重要的是第二个参数，set和map指明参数类型的时候，以第二个参数为准，这样红黑树既可以让set使用，也可以让map使用
但是问题又来了，在插入的时候需要比较大小，map传入的是一个pair对象，不能直接比较，所以第三个参数的作用就体现出来了，这是一个仿函数类，在比较的时候，创建一个仿函数对象，用仿函数去比较，如果是set，比较的是Key，如果是map，就返回Key去比较

不得不说STL这个设计，非常棒！！！！！

具体封装，直接上代码：
红黑树代码：

#pragma once
#include<iostream>
#include<assert.h>
using namespace std;namespace rb_tree
{//枚举定义节点颜色enum Colour{RED,BLACK};//红黑树节点template<class T>struct RBTreeNode{T _data;//数据RBTreeNode* _left;//左树RBTreeNode* _right;//右树RBTreeNode* _parent;//父树Colour _col;//节点颜色RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED)//节点颜色初始化为红色{}};//迭代器//                     Ref = T&  Ptr = T*template<class T,class Ref,class Ptr>struct RBTreeIterator{typedef RBTreeIterator<T, Ref, Ptr> Self;typedef RBTreeNode<T> node;node* nod;RBTreeIterator(node* root):nod(root){}Ref operator *(){return nod->_data;}Ptr operator ->(){return &(nod->_data);}bool operator !=(const Self& data){return nod != data.nod;}Self operator ++(){//如果nod的右树不为空，右树的最左节点就是下一个位置if (nod->_right){node* subleft = nod->_right;while (subleft->_left){subleft = subleft->_left;}nod = subleft;}//如果右树为空，沿着到根的路径找，子树为父树的左子树就是下一个位置else{node* cur = nod;node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}nod = parent;}return *this;}Self operator --(){//如果左树存在，左树的右节点就是上一个，否则左树就是上一个if (nod->_left){node* subright = nod->_left;while (subright->_right){subright = subright->_right;}nod = subright;}else{//向上找，如果当前节点是父树的右节点，则父树就是上一个节点node* parent = nod->_parent;node* cur = nod;while (parent && parent->_left == nod){cur = parent;parent = cur->_parent;}nod = parent;}return *this;}};template<class T, class Ref, class Ptr>struct Reverse_Iterator{typedef Reverse_Iterator<T,Ref,Ptr> Self;typedef RBTreeNode<T> node;RBTreeIterator<T,Ref,Ptr> _it;Reverse_Iterator(node* root):_it(root){}//使用正向迭代器来构造反向迭代器Ref operator *(){return _it.nod->_data;}Ptr operator ->(){return &_it->nod;}bool operator !=(const Self& data){return _it.nod != data._it.nod;}Self operator ++(){--_it;return *this;}Self operator --(){++ _it;return *this;}};template<class K, class T,class KeyOfT>class RBTree{public:typedef RBTreeNode<T> node;typedef RBTreeIterator<T, T&, T*> iterator;//迭代器typedef Reverse_Iterator<T, T&, T*>  reverse_iterator;//反向迭代器public://迭代器iterator begin(){assert(_root);//返回树的最左节点node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}reverse_iterator rbegin(){return reverse_iterator(nullptr);}reverse_iterator rend(){assert(_root);//返回树的最左节点node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return reverse_iterator(cur);}//插入bool insert(const T& data){//如果根节点为空，插入根节点，并将颜色改为黑色if (_root == nullptr){_root = new node(data);_root->_col = BLACK;return true;}//找到可以插入的地方node* cur = _root;node* parent = nullptr;KeyOfT kot;while (cur){if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}elsereturn false;}//插入并连接cur = new node(data);if (kot(parent->_data) > kot(cur->_data))parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//如果父节点是黑色，插入的节点是红色，直接返回true，不需要做处理if (parent->_col == BLACK) return true;//如果父节点是红色，开始处理while (parent && parent->_col == RED){//找到祖父节点node* grandfather = parent->_parent;//找到叔叔节点if (grandfather->_left == parent){node* uncle = grandfather->_right;//如果叔叔节点不为空且是红色if (uncle && uncle->_col == RED){//将叔叔和父节点变黑uncle->_col = parent->_col = BLACK;//将祖父节点变红grandfather->_col = RED;//继续向上调整cur = grandfather;parent = cur->_parent;}//叔叔节点存在且为黑，或者叔叔节点不存在else{//第一种情况//     g//   p   u// cif (cur == parent->_left){//对p继续右旋RotateR(parent);//再进行变色parent->_col = BLACK;grandfather->_col = RED;}//第二种情况//    g//  p   u//    celse{//先左旋parentRotateL(parent);//再右旋grandfatherRotateR(grandfather);//变色grandfather->_col = RED;cur->_col = BLACK;}break;}}//如果parent是祖父节点的右边，叔叔节点就是祖父节点的左边else{//找到叔叔节点node* uncle = grandfather->_left;//如果叔叔节点存在且为红if (uncle && uncle->_col == RED){uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}//如果叔叔节点不存在或存在且为黑else{//第一种情况//      g//    u   p//          cif (cur == parent->_right){//首先对grandfather进行左单旋RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}//第二种情况//      g//   u     p//       celse{//首先对parent进行右单旋RotateR(parent);//再对grandfather进行左单旋RotateL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}}break;}}//不论什么情况下，根节点都必须是黑色的_root->_col = BLACK;return true;}iterator find(const K& data){node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) == data) return iterator(cur);else if (kot(cur->_data) > data) cur = cur->_left;else cur = cur->_right;}return iterator(nullptr);}private://左单旋void RotateL(node* parent){node* SubR = parent->_right;node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL)SubRL->_parent = parent;node* pparent = parent->_parent;parent->_parent = SubR;SubR->_left = parent;if (pparent){if (pparent->_left == parent)pparent->_left = SubR;elsepparent->_right = SubR;SubR->_parent = pparent;}else{_root = SubR;SubR->_parent = nullptr;}}//右单旋void RotateR(node* parent){node* SubL = parent->_left;node* SubLR = SubL->_right;node* pparent = parent->_parent;parent->_left = SubLR;SubL->_right = parent;parent->_parent = SubL;if (SubLR)SubLR->_parent = parent;if (pparent){if (pparent->_left == parent)pparent->_left = SubL;elsepparent->_right = SubL;SubL->_parent = pparent;}else{_root = SubL;SubL->_parent = nullptr;}}private:node* _root = nullptr;//根节点};
}

set封装代码：

#pragma once
#include"RBTree.h"namespace myset
{template<class K>class set{public:typedef rb_tree::RBTreeIterator<K, K&, K*> iterator;typedef rb_tree::Reverse_Iterator<K, K&, K*> reverse_iterator;struct SetKeyOfT{K operator()(const K& key){return key;}};//迭代器iterator begin(){return _rb.begin();}iterator end(){return _rb.end();}reverse_iterator rbegin(){return _rb.rbegin();}reverse_iterator rend(){return _rb.rend();}bool insert(const K& data){return _rb.insert(data);}iterator find(K& data){return _rb.find(data);}private:rb_tree::RBTree<K,K,SetKeyOfT> _rb;};
}template<class K,class V>
class map
{struct MapKeyOfT{K operator()(const pair<K, V>& data){return data.first;}};
private:rb_tree::RBTree<K, pair<K, V>, MapKeyOfT> _rb;
};

map封装代码：

#pragma once
#include"RBTree.h"namespace mymap
{template<class K, class V>class map{struct MapKeyOfT{K operator()(const pair<K, V>& data){return data.first;}};public:typedef rb_tree::RBTreeIterator<pair<K, V>, pair<K, V>&, pair<K, V>*> iterator;typedef rb_tree::Reverse_Iterator<pair<K, V>, pair<K, V>&, pair<K, V>*> reverse_iterator;//迭代器iterator begin(){return _rb.begin();}iterator end(){return _rb.end();}reverse_iterator rbegin(){return _rb.rbegin();}reverse_iterator rend(){return _rb.rend();}bool insert(const pair<K, V>& data){return _rb.insert(data);}iterator find(const K& data){return _rb.find(data);}private:rb_tree::RBTree<K, pair<K, V>, MapKeyOfT> _rb;};
}