1. 归并排序

1.1 基于递归

归并排序的核心是二路归并，实现二路归并需要一个额外的辅助数组，因此空间复杂度是 $O (n)$ 。

void merge(vector<int>& a, int l, int mid, int r, vector<int>& tmp) {int i = l, j = mid + 1, k = l;while (i <= mid && j <= r) {if (a[i] <= a[j]) tmp[k++] = a[i++];else tmp[k++] = a[j++];}while (i <= mid) tmp[k++] = a[i++];while (j <= r) tmp[k++] = a[j++];for (int i = l; i <= r; i++) a[i] = tmp[i];
}

该函数会对数组 a 的 [l, mid] 和 [mid + 1, r] 两部分进行二路归并，其中辅助数组 tmp 的大小与 a 相同。

有了 merge 函数，我们就可以很方便的实现归并排序了：

void merge_sort(vector<int>& a, int l, int r, vector<int>& tmp) {if (l >= r) return;int mid = l + r >> 1;merge_sort(a, l, mid, tmp), merge_sort(a, mid + 1, r, tmp);merge(a, l, mid, r, tmp);
}

1.2 基于迭代

很明显，基于递归的实现是自顶向下的，而基于迭代的实现是自底向上的。

我们可以先枚举区间长度，再枚举区间左端点。一开始每个区间的长度是 $1$ ，我们每次对相邻的两个区间进行二路归并，每归并一次区间的长度就是原先的两倍，所以枚举区间长度时变量 len 的更新方式为 len *= 2。

对于区间左端点，每合并完两个区间后，左端点就要更新成下下个区间，如下图所示：

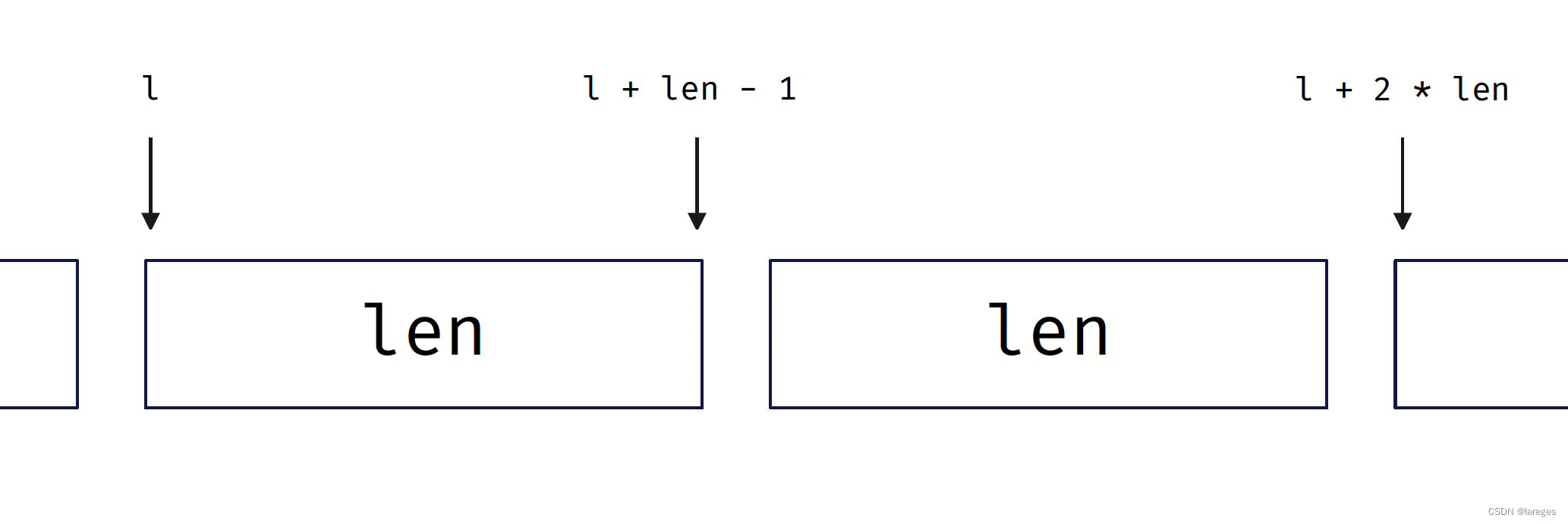
还需保证 mid < n - 1，即 l < n - len。

void merge_sort(vector<int>& a) {int n = a.size();vector<int> tmp(n);for (int len = 1; len < n; len *= 2) {for (int l = 0; l < n - len; l += 2 * len) {int mid = l + len - 1;int r = min(l + 2 * len - 1, n - 1);merge(a, l, mid, r, tmp);}}
}

归并排序的时间复杂度是 $O(n\log n)$ ，无论是递归还是迭代，空间复杂度都是 $O (n)$ 。

2. 快速排序

2.1 基于递归

void quick_sort(vector<int>& a, int l, int r) {if (l >= r) return;int mid = l + r >> 1;int i = l - 1, j = r + 1, x = a[mid];while (i < j) {while (a[++i] < x);while (a[--j] > x);if (i < j) swap(a[i], a[j]);}quick_sort(a, l, j), quick_sort(a, j + 1, r);
}

2.2 基于迭代

void quick_sort(vector<int>& a, int l, int r) {if (l >= r) return;stack<pair<int, int>> stk;stk.emplace(l, r);while (!stk.empty()) {auto [l, r] = stk.top();stk.pop();if (l < r) {int mid = l + r >> 1;int i = l - 1, j = r + 1, x = a[mid];while (i < j) {while (a[++i] < x);while (a[--j] > x);if (i < j) swap(a[i], a[j]);}stk.emplace(l, j);stk.emplace(j + 1, r);}}
}