1. 二叉树基本概念

1.1 定义

n(n≥0)个结点的有限集合，由一个根结点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。

1.2 逻辑结构：

一对二（1:2）

1.3 基本特征

每个结点最多只有两棵子树( 不存在度大于 2 的结点)；
左子树和右子树次序不能颇倒( 有序树)

1.4 基本形态：

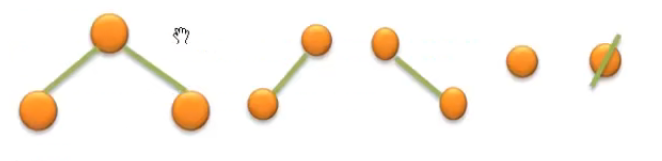
两个节点 ； 左子树；右子树； 一个节点 没有节点，空树

1.5 问题 ：（仅做了解）

具有3个节点的二叉树可能有几种不同形态？普通树呢？

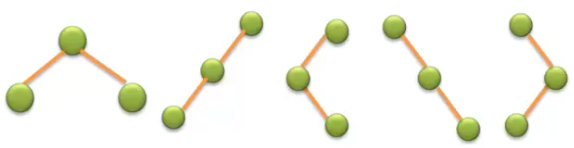
二叉树可以画出五种形态，但是普通的树只能有两种形态。

2. 二叉树性质

2.1 性质1：在二叉树第i层上至多有2的(i-1)次方个节点（i>0）

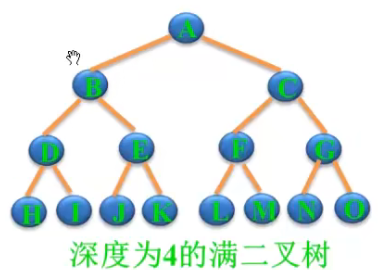
第三层对应最多有2的3-1个节点，也就是4个节点

2.2 性质2：深度为k的二叉树至多有 2的k次方-1个结点(k>0)

性质1案例中，最多的是有2的4次方-1个节点，即15

2.3 概念解释：

2.3.1 满二叉树

一棵深度为k 且有2的k次方-1个结点的二叉树。
特点：每层都“充满”了结点

2.3.2 完全二叉树(重点)

除最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干节点。

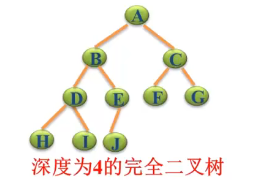
如上图中J是变为右子树的，就不是完全二叉树（因为最后一层差的是左子树），这样就可以保证将一个数组放到一个完全二叉树是没有问题的。
理解 : k-1 层与满二叉树完全相同，第 k 层结点尽力靠左

2.4 性质4：具有 n 个结点的完全二叉树的深度必为 log2n+1

2.5 性质5：对完全二叉树，若从上至下、从左至右编号，则编号为 i 的结点，其左孩子编号必为2i，其右孩子编号必为 2i + 1；其双亲的编号必为i/2(i=1 时为根，除外）

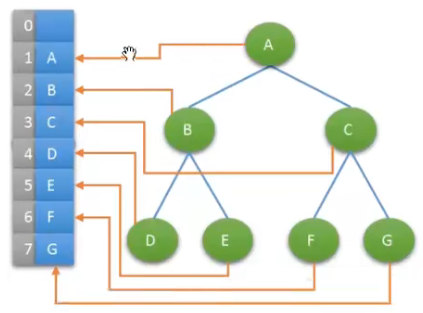
使用此性质可以使用完全二叉树实现树的顺序存储。

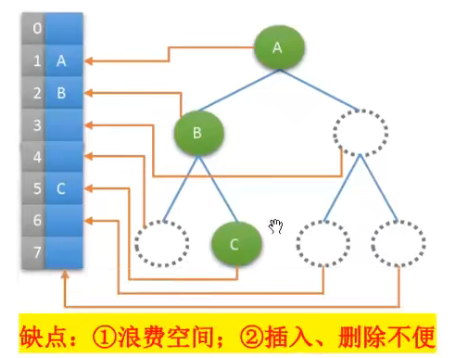
2.6 如果不是完全二叉树咋整???

将其转换成完全二叉树即可

3. 二叉树的表示

3.1 二叉链表示法

一般从根结点开始存储。相应地，访问树中结点时也只能从根开始。
增加2个指针域，一个左指针指向左孩子，一个右指针指向右孩子

3.1.1 存储结构

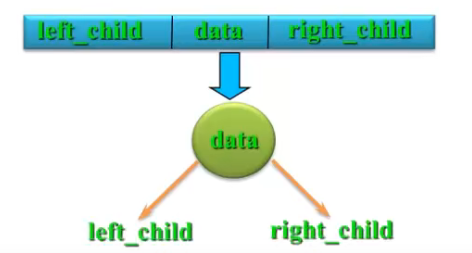
3.1.2 节点数据类型定义

typedef struct BiTNode
{int data;struct BiTNode *lchild,*rchild;
} BiTNode, *BiTree;

3.2 三叉链表示法

3.2.1 存储结构

每个节点有三个指针域，其中两个分别指向子节点(左孩子，右孩子)，还有一个指针指向该节点的父节点。

3.2.3 节点数据类型定义

typedef struct TriTNode
{int data;//左右孩子指针struct TriTNode *lchild,*rchild;struct TriTNode *parent;
} TriTNode, *TriTree;

二叉树与三叉树对比： 三叉链表示法相对于二叉链表示法，多了一个结构体指针，指向爹