全文链接：https://tecdat.cn/?p=33632

机器学习模型的表现不佳通常是由于过度拟合或欠拟合引起的，我们将重点关注客户经常遇到的过拟合情况（点击文末“阅读原文”获取完整代码数据）。

相关视频

过度拟合是指学习的假设在训练数据上拟合得非常好，以至于对新数据的模型性能造成负面影响。该模型对于训练数据中没有的新实例的泛化能力较差。

复杂模型，如随机森林、神经网络和XGBoost，更容易出现过度拟合。简单模型，如线性回归，也可能出现过度拟合——这通常发生在训练数据中的特征数量多于实例数量时。

如何检测过度拟合？

最基本的交叉验证实现类型是基于保留数据集的交叉验证。该实现将可用数据分为训练集和测试集。要使用基于保留数据集的交叉验证评估我们的模型，我们首先需要在保留集的训练部分上构建和训练模型，然后使用该模型对测试集进行预测，以评估其性能。

我们了解了过度拟合是什么，以及如何使用基于保留数据集的交叉验证技术来检测模型是否过度拟合。让我们获取一些数据，并在数据上实施这些技术，以检测我们的模型是否过度拟合。

python
# 导入库
import pandas as pdfrom sklearn.model_selection import train_test_split# 加载数据集
df = pd.DataFrame(data= dataset.data)# 将目标标签添加到数据框中
df["target"] = dataset.target# 分离特征和目标标签
X = df.iloc[:, :-1]# 分割训练集和测试集（基于保留数据集的交叉验证）
X_train, X_test, y_train, y_test = train_test_split(X, y,# 实例化模型
clf = RandomForestClassifier(random_state=24)# 绘制学习曲线
plot_learning_curves(X_train=X_train,y_train=y_train,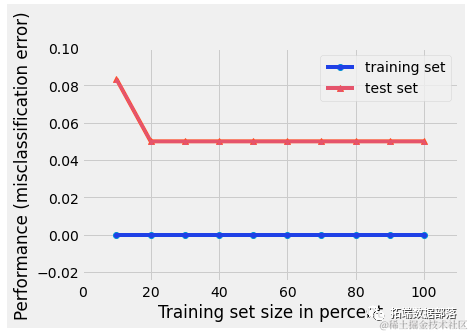

在上面的图片中，我们可以清楚地看到我们的随机森林模型对训练数据过度拟合。我们的随机森林模型在训练集上有完美的分类错误率，但在测试集上有0.05的分类错误率。这可以通过散点图上两条线之间的间隙来说明。

---

点击标题查阅往期内容

PYTHON链家租房数据分析：岭回归、LASSO、随机森林、XGBOOST、KERAS神经网络、KMEANS聚类、地理可视化

左右滑动查看更多

01

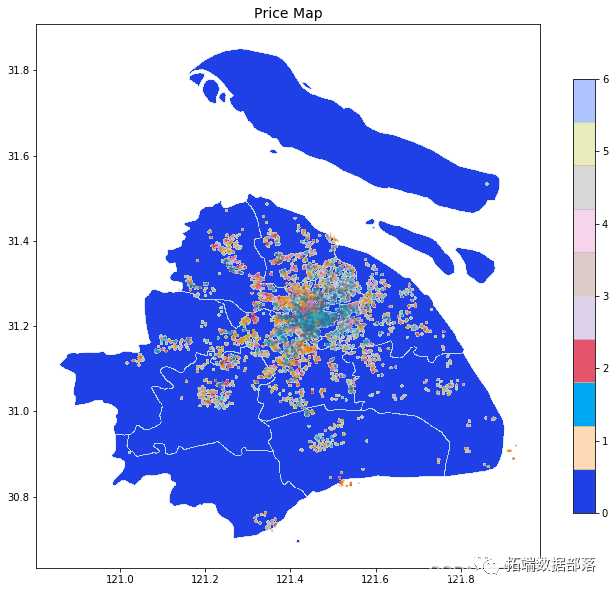
02

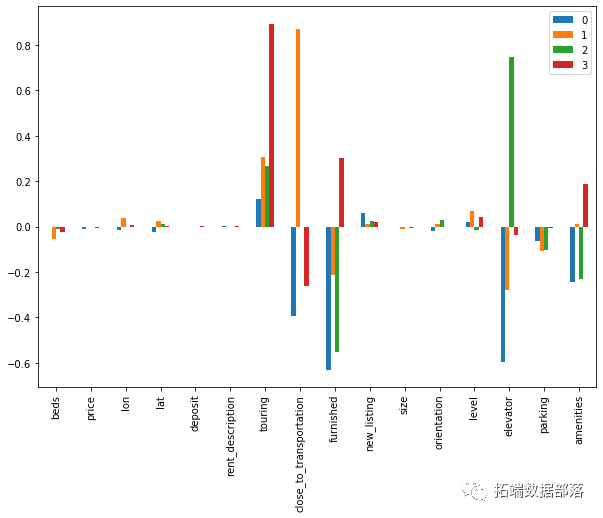
03

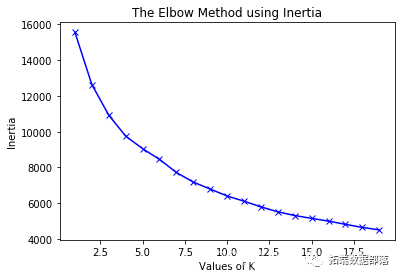
04

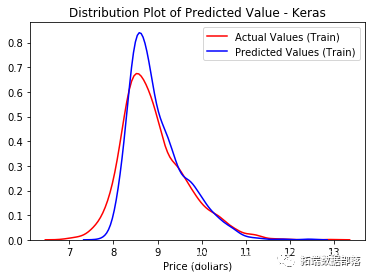
另外，我们可以通过改进模型来对抗过度拟合。我们可以通过减少随机森林或XGBoost中的估计器数量，或者减少神经网络中的参数数量来简化模型。我们还可以引入一种称为“提前停止”的技术，即在达到设定的训练轮次之前提前停止训练过程。

另一种简化模型的方法是通过正则化向模型中添加偏差。

正则化是什么，为什么我们需要它？

正则化技术在机器学习模型的开发中起着至关重要的作用。尤其是复杂模型，如神经网络，容易过拟合训练数据。从数学或机器学习的角度来看，"regularize"一词表示我们正在使某个东西规则化。在数学或机器学习的上下文中，我们通过添加信息来使某个东西规则化，以创建一个可以防止过拟合的解决方案。在我们的机器学习上下文中，我们要使某个东西规则化的是"目标函数"，即我们在优化问题中尝试最小化的东西。

优化问题

为了获得我们模型的"最佳"实现，我们可以使用优化算法来确定最大化或最小化目标函数的一组输入。通常，在机器学习中，我们希望最小化目标函数以降低模型的误差。这就是为什么目标函数在从业者中被称为损失函数的原因，但也可以称为成本函数。

有大量流行的优化算法，包括：

• 斐波那契搜索

• 二分法

• 线性搜索

• 梯度下降

• ...等等

没有正则化的梯度下降

梯度下降是一种一阶优化算法。它涉及采取与梯度相反方向的步骤，以找到目标函数的全局最小值（或非凸函数的局部最小值）。

要用数学方式表达梯度下降的工作原理，假设N是观测值的数量，Y_hat是实例的预测值，Y是实例的实际值。

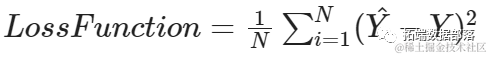
为了确定要采取的步长（大小）以及方向，我们计算：

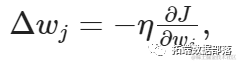
其中η是学习率 - 学习率是优化算法中的一个调节参数，它确定每次迭代时向最小损失函数的最小值移动的步长[来源: Wikipedia]。然后，在每次迭代之后，更新模型的权重，更新规则如下：

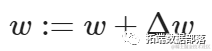
其中Δw是一个包含每个权重系数w的权重更新的向量。下面的函数演示了如何在Python中实现不带任何正则化的梯度下降优化算法。

为了更好地理解这一点，让我们构建一个人工数据集和一个没有正则化的线性回归模型来预测训练数据。

python
# 导入所需模块import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error# 加载数据df = pd.read_csv# 选择一个特征
# 为了简单起见，只使用100个实例
X = df.loc[:100, 5]
y = df.loc[:100, 13] # 目标标签# 重塑数据
X_reshaped = X[:, np.newaxis]
y_reshaped = y[:, np.newaxis]# 实例化线性回归模型
linear_regression = LinearRegression()# 训练模型
linea# 进行预测
y_p# 评估模型
mse = mea_squared_rrr(_esaped y_red)
print(f"均方误差：{mse}\n")# 绘制最佳拟合线
sns.sca
plt.title("无正则化的线性回归模型")>>>> 均方误差：9.7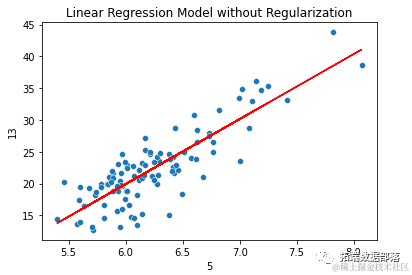

L1 正则化

L1 正则化，也被称为 L1 范数或 Lasso（在回归问题中），通过将参数收缩到0来防止过拟合。这使得某些特征变得不相关。

例如，假设我们想使用机器学习来预测房价（查看文末了解数据免费获取方式）。考虑以下特征：

• Street – 道路通行能力，

• Neighborhood – 物业位置，

• Accessibility – 交通便利程度，

• Year Built – 房屋建造年份，

• Rooms – 房间数量，

• Kitchens – 厨房数量，

• Fireplaces – 房屋中的壁炉数量。

当预测房屋价值时，直觉告诉我们不同的输入特征对价格的影响不同。例如，与壁炉数量相比，社区或房间数量对房价的影响更大。

数学上，我们通过扩展损失函数来表达 L1 正则化：

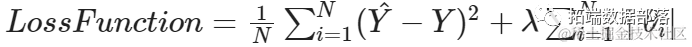
实质上，当我们使用L1正则化时，我们对权重的绝对值进行惩罚。

尽管如此，在我们的示例回归问题中，Lasso回归（带有L1正则化的线性回归）将产生一个高度可解释的模型，并且只使用了输入特征的子集，从而降低了模型的复杂性。

以下是Python中使用Lasso回归的示例代码：

python
import warnings
warnings.filterwarnings("ignore")import numpy as npfrom sklearn.metrics import mean_squared_error# 加载数据df = pd.read_csv(URL, header=None)# 选择单个特征（为简单起见，仅使用100个实例）
y = df.loc[:100, 13] # 目标标签 # 重塑数据
y_reshaped = y[:, np.newaxis]# 实例化Lasso回归模型
lasso = Lasso# 训练模型
lassped)# 进行预测
y_predict(X_eshed)# 评估模型
print(f"均方误差：{mse}")
print(f"模型系数：{lasso.coef_}\n")# 绘制最佳拟合线
plt.title("带有L1正则化的线性回归模型（Lasso）")
plt.show()

输出结果为：

均方误差：34.7
模型系数：[0.]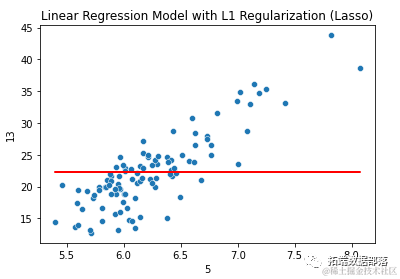

L2正则化

L2正则化，也被称为L2范数或Ridge（在回归问题中），通过将权重强制变小来防止过拟合，但不会使其完全为0。

在执行L2正则化时，我们在损失函数中添加的正则化项是所有特征权重的平方和：

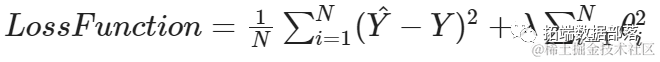
L2正则化返回的解决方案是非稀疏的，因为权重不会为零（尽管某些权重可能接近于0）。

L1正则化和L2正则化的区别：

• L1正则化对权重的绝对值之和进行惩罚，而L2正则化对权重的平方和进行惩罚。

• L1正则化的解是稀疏的，而L2正则化的解是非稀疏的。

• L2正则化不进行特征选择，因为权重只会被减小到接近于0的值，而不是变为0。L1正则化内置了特征选择功能。

• L1正则化对异常值具有鲁棒性，而L2正则化没有。

Python中Ridge回归的示例代码：

pythonfrom sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.metrics import mean_squared_error# 加载数据df = pd.read_csv(URL, header=None)# 为简单起见，选择一个特征和100个实例
y = df.loc[:100, 13] # 目标标签# 重塑数据
X_reshaped = X[:, np.newaxis]# 实例化、训练和推断
ridge = Rdge(apha=100)print(f"均方误差：{mse}")
print(f"模型系数：{ridge.coef_}\n")sns.scatterplot(X,y)
plt.title("带有L2正则化（Ridge）的线性回归模型")
plt.show()>>>> 均方误差：25.96309109305436
模型系数：[[1.98542524]]

观察Ridge回归模型中的alpha值，它为100。超参数alpha值越大，权重值越接近于0，但不会变为0。

L1正则化和L2正则化哪个更好？

哪种正则化方法更好是一个供学者们争论的问题。然而，作为实践者，在选择L1和L2正则化之间需要考虑一些重要因素。我将它们分为6个类别，并告诉你每个类别哪个解决方案更好。

哪个解决方案更鲁棒？L1

L1正则化比L2正则化更具鲁棒性，原因是L2正则化对权重进行平方处理，因此数据中的异常值的代价呈指数增长。L1正则化对权重取绝对值，所以代价只会线性增长。

哪个解决方案具有更多可能性？L1

我指的是到达一个点的解决方案的数量。L1正则化使用曼哈顿距离到达一个点，所以有很多路线可以走到达一个点。L2正则化使用欧几里得距离，这将告诉您最快到达某个点的方法。这意味着L2范数只有一个可能的解决方案。

如前所述，L2正则化仅将权重缩小到接近于0的值，而不是真正变为0。另一方面，L1正则化将值收缩到0。这实际上是一种特征选择的形式，因为某些特征完全从模型中删除了。

总结

在本文中，我们探讨了过拟合是什么，如何检测过拟合，损失函数是什么，正则化是什么，为什么需要正则化，L1和L2正则化的工作原理以及它们之间的区别。

数据获取

在公众号后台回复“房价数据”，可免费获取完整数据。

本文中分析的房价数据分享到会员群，扫描下面二维码即可加群！

点击文末“阅读原文”

获取全文完整代码数据资料。

本文选自《Python用正则化Lasso、岭回归预测房价、随机森林交叉验证鸢尾花数据可视化2案例》。

点击标题查阅往期内容

R语言贝叶斯广义线性混合（多层次/水平/嵌套）模型GLMM、逻辑回归分析教育留级影响因素数据

Python中的Lasso回归之最小角算法LARS

高维数据惩罚回归方法：主成分回归PCR、岭回归、lasso、弹性网络elastic net分析基因数据

Python高维变量选择:SCAD平滑剪切绝对偏差惩罚、Lasso惩罚函数比较

R语言惩罚logistic逻辑回归（LASSO,岭回归）高维变量选择的分类模型案例

R使用LASSO回归预测股票收益

广义线性模型glm泊松回归的lasso、弹性网络分类预测学生考试成绩数据和交叉验证

贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据

R语言RSTAN MCMC：NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据

r语言中对LASSO回归，Ridge岭回归和弹性网络Elastic Net模型实现

R语言高维数据惩罚回归方法：主成分回归PCR、岭回归、lasso、弹性网络elastic net分析基因数据（含练习题）

Python中LARS和Lasso回归之最小角算法Lars分析波士顿住房数据实例

R语言Bootstrap的岭回归和自适应LASSO回归可视化

R语言Lasso回归模型变量选择和糖尿病发展预测模型

R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析

基于R语言实现LASSO回归分析

R语言用LASSO，adaptive LASSO预测通货膨胀时间序列

R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析

R语言惩罚logistic逻辑回归（LASSO,岭回归）高维变量选择的分类模型案例

Python中的Lasso回归之最小角算法LARS

r语言中对LASSO回归，Ridge岭回归和弹性网络Elastic Net模型实现

r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

R语言实现LASSO回归——自己编写LASSO回归算法

R使用LASSO回归预测股票收益

python使用LASSO回归预测股票收益

Python中LARS和Lasso回归之最小角算法Lars分析波士顿住房数据实例

R语言Bootstrap的岭回归和自适应LASSO回归可视化

R语言Lasso回归模型变量选择和糖尿病发展预测模型

R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析

基于R语言实现LASSO回归分析

R语言用LASSO，adaptive LASSO预测通货膨胀时间序列

R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析

R语言惩罚logistic逻辑回归（LASSO,岭回归）高维变量选择的分类模型案例

Python中的Lasso回归之最小角算法LARS

r语言中对LASSO回归，Ridge岭回归和弹性网络Elastic Net模型实现

r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

R语言实现LASSO回归——自己编写LASSO回归算法

R使用LASSO回归预测股票收益

python使用LASSO回归预测股票收益

R语言随机森林RandomForest、逻辑回归Logisitc预测心脏病数据和可视化分析

数据分享|R语言逻辑回归、线性判别分析LDA、GAM、MARS、KNN、QDA、决策树、随机森林、SVM分类葡萄酒交叉验证ROC

MATLAB随机森林优化贝叶斯预测分析汽车燃油经济性

R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数

R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病

R语言中贝叶斯网络（BN）、动态贝叶斯网络、线性模型分析错颌畸形数据

R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

Python贝叶斯回归分析住房负担能力数据集

R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析

Python用PyMC3实现贝叶斯线性回归模型

R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型

R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

R语言和STAN,JAGS：用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据

R语言基于copula的贝叶斯分层混合模型的诊断准确性研究

R语言贝叶斯线性回归和多元线性回归构建工资预测模型

R语言贝叶斯推断与MCMC：实现Metropolis-Hastings 采样算法示例

R语言stan进行基于贝叶斯推断的回归模型

R语言中RStan贝叶斯层次模型分析示例

R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化

R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样

R语言贝叶斯推断与MCMC：实现Metropolis-Hastings 采样算法示例

R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化

视频：R语言中的Stan概率编程MCMC采样的贝叶斯模型

R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计

R语言用lme4多层次（混合效应）广义线性模型（GLM），逻辑回归分析教育留级调查数据

R语言随机森林RandomForest、逻辑回归Logisitc预测心脏病数据和可视化分析

R语言基于Bagging分类的逻辑回归(Logistic Regression)、决策树、森林分析心脏病患者

R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化