Plancherel定理是调和分析里的一个结论, 最早由Michel Plancherel证明, 其可表述为
对同时属于 L 1 ( R ) L^{1}(R) L1(R) 和 L 2 ( R ) L^{2}(R) L2(R) 的函数f来说,其傅立叶变换F属于 L 2 ( R ) L^{2}(R) L2(R) ,且傅立叶变换是等距变换.数学表述为:
∥ f ^ ∥ 2 = ∫ − ∞ ∞ f 2 ( t ) d t , \Vert \hat{f}\Vert^{2}=\int_{-\infty}^{\infty}f^{2}(t)dt, ∥f^∥2=∫−∞∞f2(t)dt,
它指出一个函数的 L 2 L^{2} L2范数等于其傅里叶频谱的 L 2 L^{2} L2范数。更精确地表述为,如果一个函数同时属于 L 1 L^{1} L1空间和 L 2 L^{2} L2空间,那么其傅里叶变换属于 L 2 L^{2} L2空间,且傅里叶变换对 L 2 L^{2} L2范数是等距映射。这表明限制在 L 1 L^{1} L1∩ L 2 L^{2} L2上的傅里叶变换可以扩展为一个唯一的等距映射 L 2 L^{2} L2→ L 2 L^{2} L2,该映射实际上为一个酉映射。
傅里叶变换的酉性在科学和工程领域中通常称为帕萨瓦尔定理( Parseval’s theorem)。
在数学上,帕塞瓦尔定理经常指"0黑吐转换是幺正篡符"这…结论;简而言之,就是说函数平方的和(或积分)等于其傅里叶转换式平方之和(或者积分)。这个定理产生于Marc-Antoine Parseval在1799年所得到的一个有关级数的定理,该定理随后被应用于傅里叶级数。它也被称为瑞利能量定理或瑞利恒等式,以物理学家约翰·斯特拉特,第三代瑞利男爵命名。

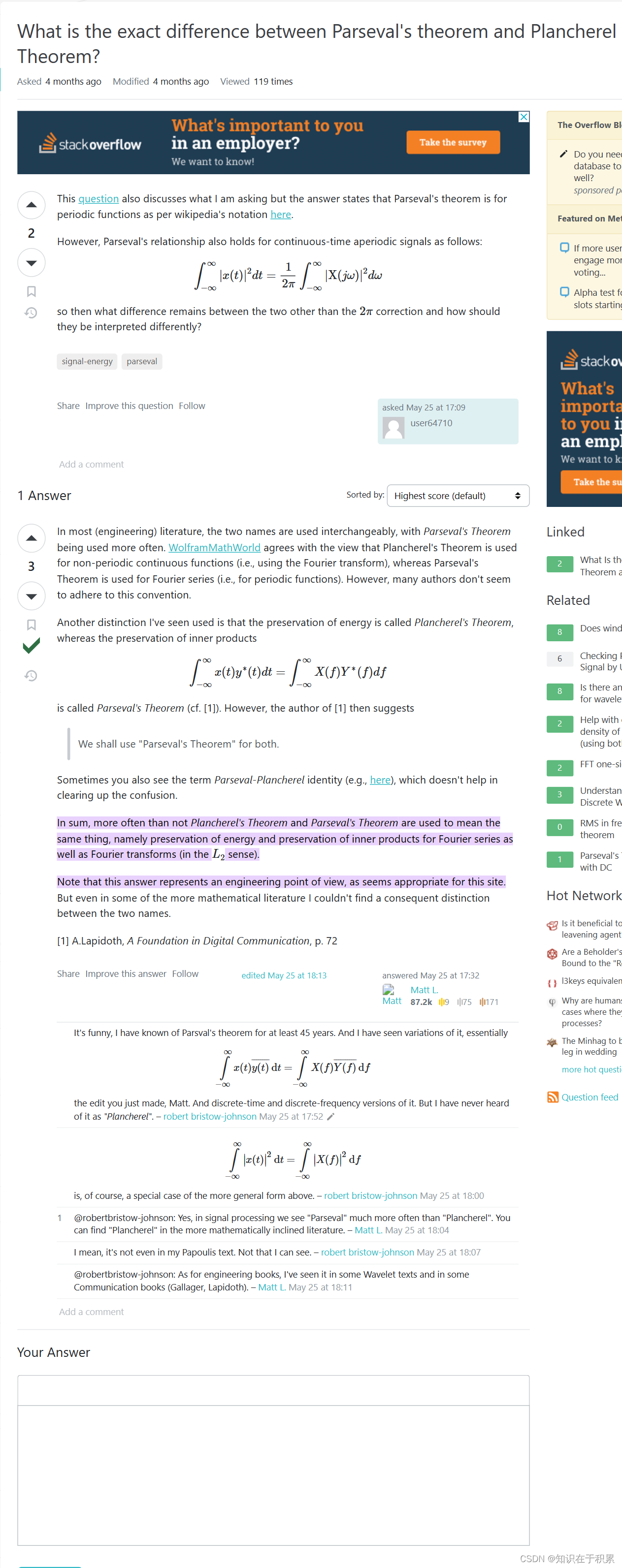
See https://dsp.stackexchange.com/questions/87977/what-is-the-exact-difference-between-parsevals-theorem-and-plancherel-theorem#:~:text=In%20sum%2C%20more%20often%20than%20not%20Plancherel%27s%20Theorem,of%20view%2C%20as%20seems%20appropriate%20for%20this%20site.

See https://www.princeton.edu/~cuff/ele301/files/lecture8_2.pdf


![[管理与领导-102]:经营与管理的关系:攻守关系;武将文官关系;开疆拓土与守护城池的关系;战斗与练兵的关系;水涨船高,水落船低的关系。](https://img-blog.csdnimg.cn/15882cfb98834563a56d0040cff25b15.png)