一 说明
最近对CNN架构的研究包括许多不同的卷积变体,这让我在阅读这些论文时感到困惑。我认为通过一些更流行的卷积变体的精确定义,效果和用例(在计算机视觉和深度学习中)是值得的。这些变体旨在保存参数计数、增强推理并利用目标问题的某些特定特征。
这些变体中的大多数都简单易懂,因此我专注于了解每种方法的优点和用例。这些知识有望帮助您了解最新CNN架构背后的直觉,并帮助您设计自己的网络。
二 卷 积
让我们简要概述一下卷积的基本形式。根据PapersWithCode中的描述,
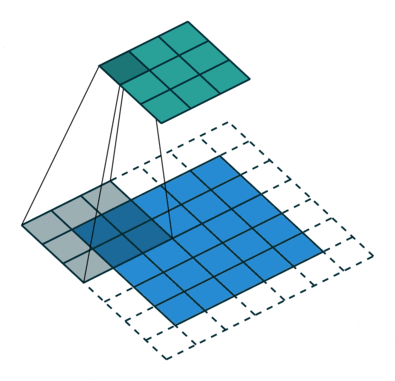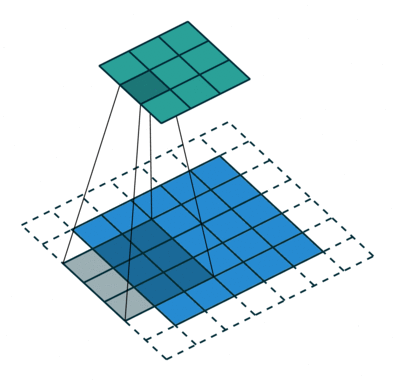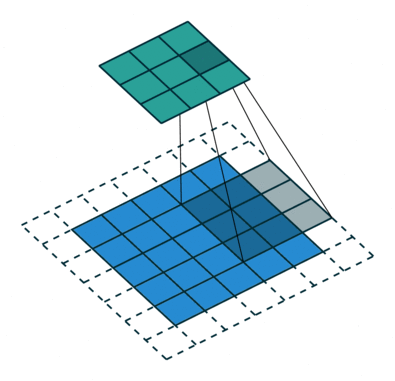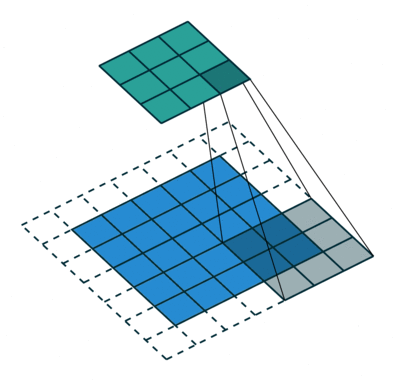
卷积是一种矩阵运算,由一个内核组成,一个小的权重矩阵,它滑过输入数据,执行逐元素乘法与它所在的输入部分,然后将结果相加到输出中。
此类操作对于处理图像是有利的,因为:
- 它们的参数效率非常高,因为图像的不同位置共享相同的权重,因此参数的数量与图像大小不成比例。
- 卷积基本上是翻译不变的。也就是说,输出不受图像中常见的小翻译和大翻译的影响,这与 MLP 不同,MLP 通常会给出非常不同的 1 像素翻译结果。
卷积的输出形状和复杂性可以使用以下参数进行配置:
- 内核大小:内核的维度,通常使用内核大小 (3×3)。
- 填充:如何填充图像的边缘以保持卷积后的图像大小。例如,上面的演示使用 1 个像素的填充。描述像素数和填充这些像素的规则。
- 步幅:扫描图像时内核的步长。通常设置为 1 以保持数据形状,设置为 2 表示对其进行缩减采样。上面的演示使用步幅为 2。

来源:伊莱·本德尔斯基
通过组合通过不同内核卷积的每个通道的结果来预测每个输出通道。因此,需要C_in形状为K×K的内核来计算一个输出通道。其中 K 表示内核大小和C_in,C_out分别表示输入和输出通道的数量。
# 参数:K×K×C_in×C_out
计算:H×W×C_in×C_out×K×K(在步幅=1的情况下)
用例:这种卷积层几乎用于计算机视觉的每个子任务。其中包括监督任务,如图像和视频分类、对象检测、分割和合成任务,如图像生成、图像超分辨率、图像到图像传输。还有一些视觉之外的应用,例如用于序列建模的 1D 卷积和 3D 相关应用。
三 逐点卷积(1x1卷积)
逐点卷积是具有 1×1 个内核的卷积层的另一个词。它们也表示为通道或投影层上的卷积。到底为什么有人会使用它?有两种主要用例:
- 用于更改输入的维度(即多个通道)。
- 一些网络(如 Inception)连接从不同内核计算的特征,这会导致通道过多,因此应用逐点卷积来管理通道数。
- 当使用逐点卷积压缩特征时,计算密集型模块(如挤压和激励)等自注意力模块更可行。
- 当将两个内积与元素总和或乘积组合时,我们有时需要匹配通道数。
该操作可以看作是沿输入特征图的深度计算多个加权和。它可以有效地总结它们。
2. 它以微不足道的成本创建通道依赖关系。通过与缺乏这种依赖性的深度卷积相结合,可以特别利用这一点。
# 参数:C_in×C_out
计算:高××C_in×C_out
四 转置卷积(反卷积/逆卷积)
反卷积显式计算卷积层的数学逆。虽然它广泛用于类视觉或信号处理,但它在深度学习中并不重要,因为可以通过梯度下降来学习操作的参数。
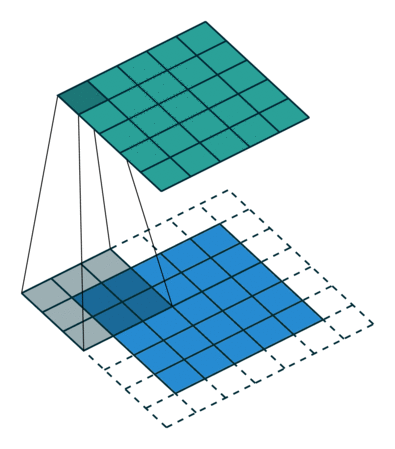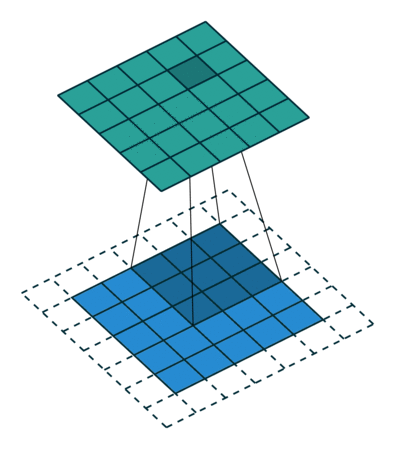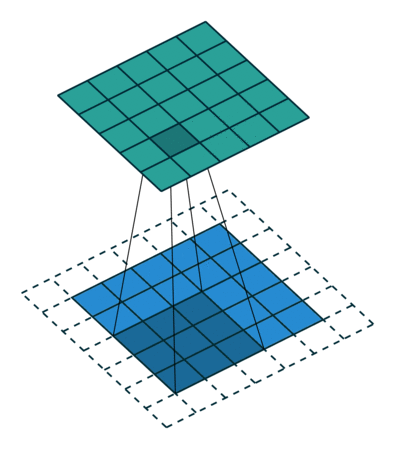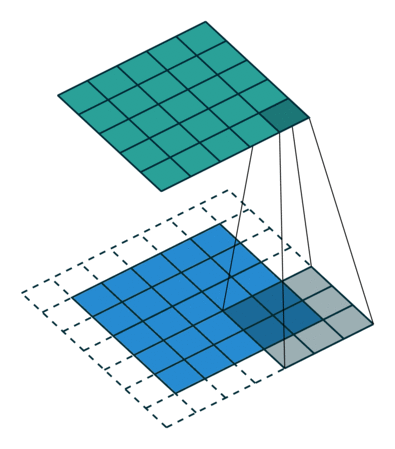
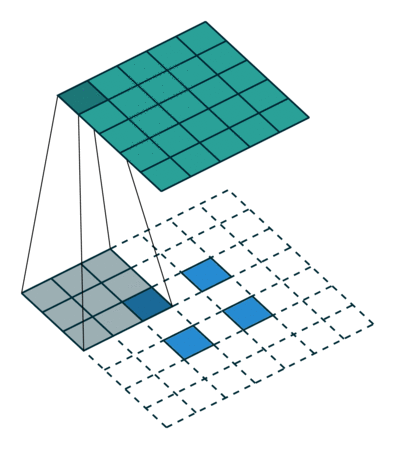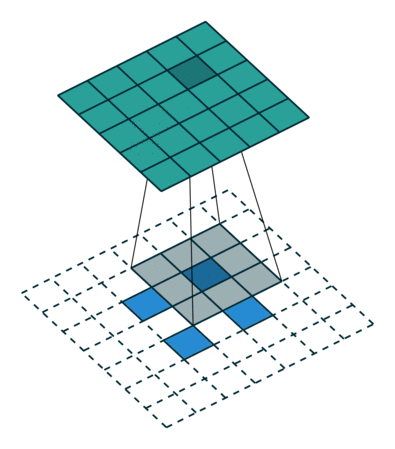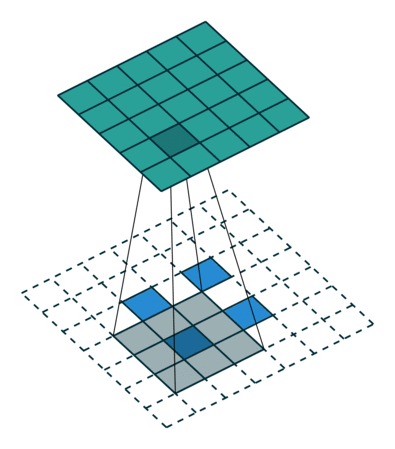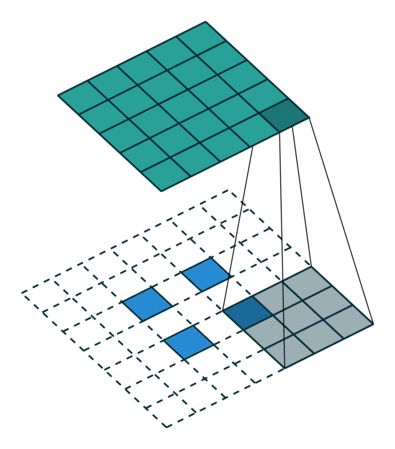
左:步幅=1,右:步幅=2
转置卷积是一种使用卷积对图像大小进行上采样的更简单方法。该操作与步幅为 1(左)时的经典卷积没有什么不同。对于 n>1 的步幅,输出形状将扩展 n 倍。这是通过在像素之间填充 0 以创建所需大小的扩展图像并对扩展图像执行卷积来完成的。
虽然转置卷积不会隐式计算卷积的逆运算,但对于深度学习来说并不重要,因为所需的滤波器(可能是逆滤波器)总是可以通过梯度下降来学习。它充分实现了增加数据空间大小的功能。
重要提示:虽然它们经常被混淆,但转置卷积不是反卷积/逆卷积。
# 参数:K×K×C_in×C_out)
用例:转置卷积用于需要上采样的网络架构。一些示例是用于语义分割、自动编码器或图像合成和生成网络的编码器-解码器样式网络中的用法。转置卷积的一个问题是棋盘伪影,这可能会给图像生成/合成带来问题。该主题超出了本文的范围,值得拥有自己的主题。有关更多信息,请参阅谷歌大脑的这篇文章。
来源:
- https://en.wikipedia.org/wiki/Deconvolution
- https://medium.com/@marsxiang/convolutions-transposed-and-deconvolution-6430c358a5b6
- https://naokishibuya.medium.com/up-sampling-with-transposed-convolution-9ae4f2df52d0
四 扩张卷积(Atrous convolution)
感受野是模型可以参考的原始图像的范围,用于对该步骤的一个像素进行推理。例如,具有一个 3×3 卷积的模型的输出可以考虑来自相对于每个像素的空间位置的 3 像素感受野的信息,而具有两个 3×3 卷积的模型具有相对于该位置的 5 像素的感受野。
增加核大小是增加感受野的一种方法,但计算量也很快增加。对图像进行下采样还具有增加感受野的效果,因为例如 3××3 特征图中的 8 卷积覆盖了更多的图像。三个 8×3 卷积足以考虑整个图像,以便在 3×8 特征空间中进行推理。
在较低空间维度上计算特征对于图像分类来说大多是可以的,但它会导致具有高分辨率输出的任务(尤其是语义分割)的大量信息丢失。
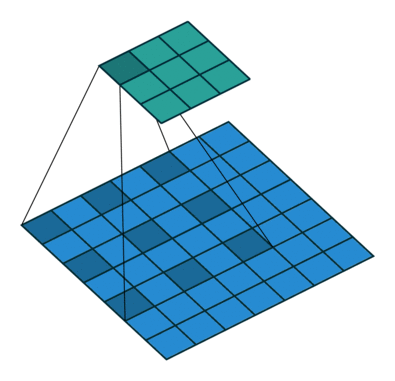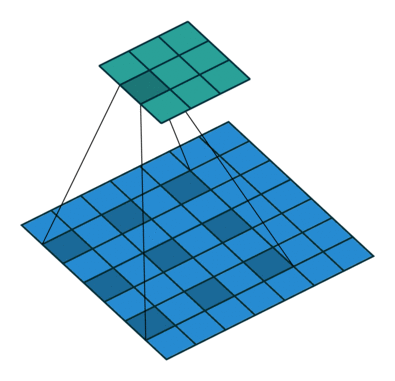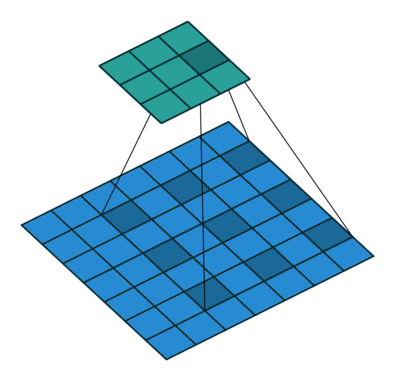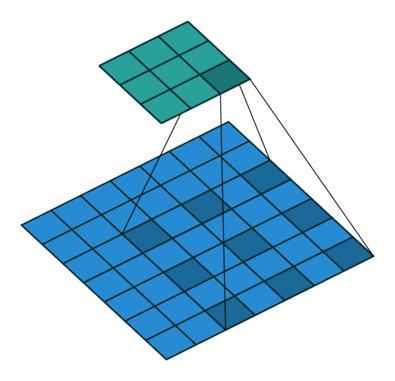
扩张卷积是一种卷积,其中内核的像素间隔(用 0 填充)。间距也被视为一个超参数,其值通常从上面演示中的 2 到大空间(如 DeepLab 模型中的 24)不等。它增加了内核大小,而不会增加计算量。这种设计能够从更大的感受野进行极其高效的计算,而不会丢失信息或增加层数。
用例:显示了语义分割中最重要的用法,但在轻量级/移动 CNN 架构中也考虑了其他任务。
提议于:通过扩张卷积进行多尺度上下文聚合
五 空间可分离卷积(Separable Convolution)
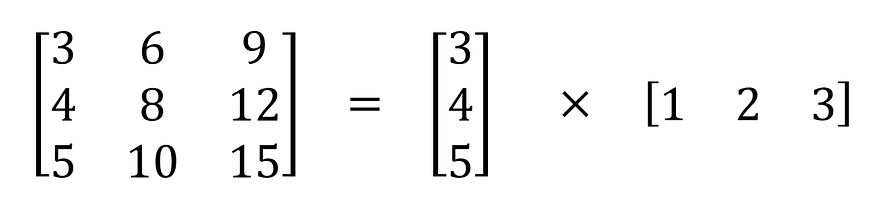
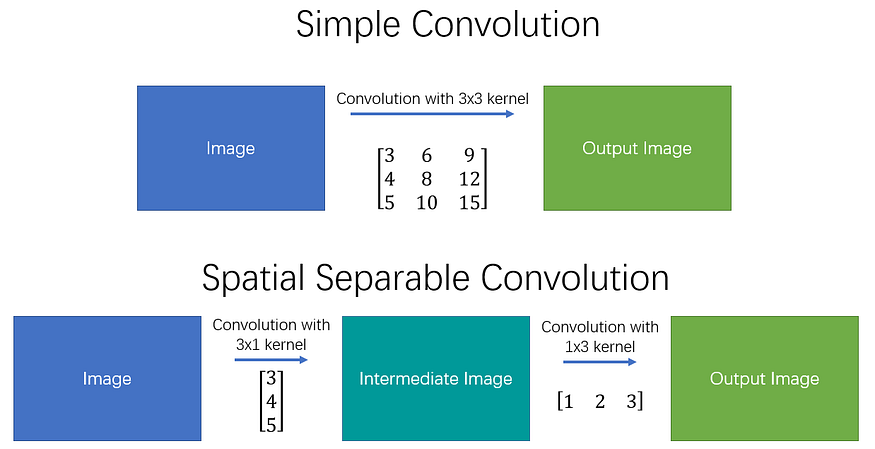
一些 3×3 矩阵可以表示为两个向量的矩阵乘法。由于 3×3 核也是一个常见矩阵,因此可以将其拆分为一个 3×1 和一个 1×3 核,但执行相同的操作。
Source: Chi-Feng Wang
具体来说,空间可分卷积将原始卷积替换为上图所述的两个阶段。这样,每个内核的参数数和操作数从 9(3×3) 减少到 6。然而,众所周知,并非所有 3×3 核都可以分离,因此空间可分离卷积可能会限制模型的能力。
# 参数:(K+K)×C_in×C_out
计算: H×W×C_in×C_out×(K+K)
用例:由于参数计数要小得多,因此有时将空间可分离卷积用于模型压缩和轻量级架构。
源:
- https://towardsdatascience.com/a-basic-introduction-to-separable-convolutions-b99ec3102728
- [Deep Learning] 딥러닝에서 사용되는 다양한 Convolution 기법들 — Enough is not enough
六 深度卷积
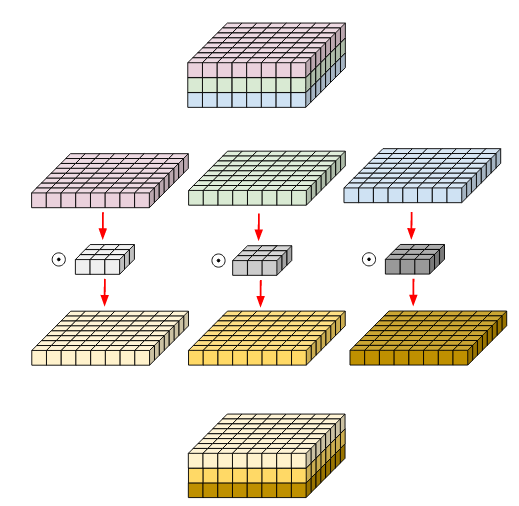
不是卷积和组合每个通道的结果,而是在每个通道上独立执行深度卷积,并将结果堆叠。我们可以直观地看到,这只有在输入和输出通道的数量一致时才有效。
深度卷积具有很高的参数和计算效率,因为参数的数量和计算复杂度都除以输出通道的数量,输出通道的数量通常范围高达 1024。但是,速度优势与操作数量的减少不成正比,因为深度卷积不像现代硬件上的传统卷积那样优化。
# 参数:K×K×C_in
计算:H×W×C_in×K×K
用例:深度卷积是构建更复杂的变体和卷积块的关键组件,这些变体和卷积块具有参数和计算效率。
七 深度可分离卷积
深度卷积,然后是逐点卷积。由于深度卷积在通道之间没有连接,因此我们使用逐点卷积将它们连接起来。Xception的作者发现将非线性放在深度卷积之后很有用。整个过程如下图所示。
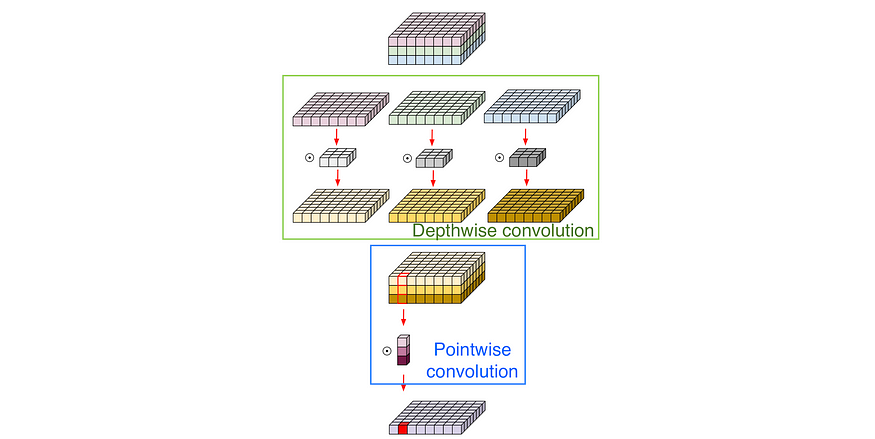
空间可分卷积将经典卷积中的 x 轴和 y 轴分开。在这种情况下,深度可分离卷积可以被视为分离通道维度。
与普通的深度卷积相比,计算复杂性略有增加,尽管仍然比传统卷积小得多。然而,与普通的深度卷积不同,它在许多经验实验中有效地模仿了常规卷积,并广泛用于现代CNN架构。
# 参数:(K×K+C_out)×C_in
计算: H×W×C_in×(K×K+C_out)
用例:Xception,MobileNet V1 / V2,EfficientNet V1(MnasNet)/ V2等等...
您可以在以下第 2 部分找到深度可分卷积的复杂历史:Xception:使用深度可分卷积进行深度学习
在这篇文章中,我们回顾了在某些情况下被提议取代传统卷积层的卷积变体列表。这些块各有优缺点,用于解决不同的问题。在后续的文章中,我们将回顾卷积设计,这些设计将进一步增强我们创建CNN架构的工具箱。
请在评论中告诉我有关建议或问题的信息。我会尽量在最多2天内回复你们所有人。