---

一、概述

1.1 概念说明

 1. 用多边形顶点的逆时针序列表示凸多边形，即P={V0, V1, … Vn-1, Vn}表示具有n+1条边的凸多边形。

 2. 若Vi和Vj是多边形上不相邻的两个顶点，则线段ViVj称为多边形的一条弦。

 3. 多边形的三角剖分是将多边形分割成互不相交的三角形。

 4. 由多边形的边和弦组成三角形上的权w(即三边和)。要求确定该凸多边形的一个三角剖分，使得该三角剖分中的所有三角形上权之和最小。

1.2 与矩阵连乘对应关系

 1. 一个矩阵连乘表达式的完全加括号方式相应于一棵完全二叉树，称为表达式的语法树。 例如，完全加括号的6矩阵连乘积((A1(A2A3))(A4(A5A6)))所相应的语法树如图(a)所示。

 2. 凸多边形{V0, V1, … Vn}的三角剖分也可以用语法树表示。例如图 (b)中7顶点的凸多边形的三角剖分可用图 (a)所示的语法树表示。

 矩阵Ai对应多边形中的一条边Vi-1 Vi。一条弦ViVj，i<j，对应矩阵连乘积A[i+1: j]。

1.3 递归定义

 1. 定义t[i][j]，1≤i<j≤n为凸子多边形{Vi-1, Vi ,…, Vj}的最优三角剖分所对应的权函数值，即其最优值。

 2. 设退化的多边形即只有一条边{Vi-1, Vi}，其权函数值为0，即t[i][i]=0。

 3. 目标：凸(n+1)边形的最优权值为t[1][n]。当i<j 时，凸子多边形至少有3个顶点。

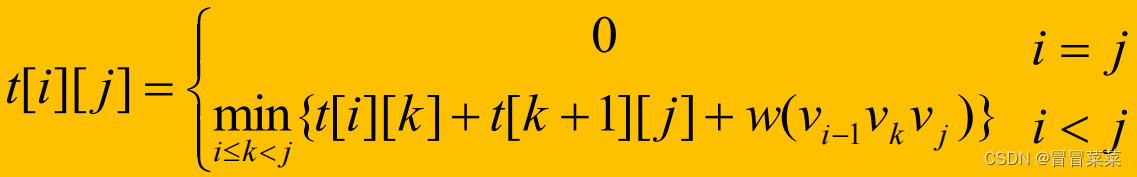
二、代码

#include <iostream> 
using namespace std;const int N = 7;//凸多边形边数+1
int weight[][N] = { { 0,2,2,3,1,4 },{ 2,0,1,5,2,3 },{ 2,1,0,2,1,4 },{ 3,5,2,0,6,2 },{ 1,2,1,6,0,1 },{ 4,3,4,2,1,0 } };//凸多边形的权int MinWeightTriangulation(int n, int **t, int **s);
void Traceback(int i, int j, int **s);//构造最优解
int Weight(int a, int b, int c);//权函数int main()
{int **s = new int *[N];int **t = new int *[N];for (int i = 0; i<N; i++){s[i] = new int[N];t[i] = new int[N];}cout << "此多边形的最优三角剖分权值为：" << MinWeightTriangulation(N - 1, t, s) << endl;cout << "最优三角剖分结构为：" << endl;Traceback(1, 5, s); //s[i][j]记录了Vi-1和Vj构成最优三角形的第3个顶点的位置return 0;
}int MinWeightTriangulation(int n, int **t, int **s)
{for (int i = 1; i <= n; i++){t[i][i] = 0;}for (int r = 2; r <= n; r++) //r为当前计算的链长（子问题规模）,即vi...vj的长度  {for (int i = 1; i <= n - r + 1; i++)//n-r+1为最后一个r链的前边界  {int j = i + r - 1;//计算前边界为r，链长为r的链的后边界  t[i][j] = t[i + 1][j] + Weight(i - 1, i, j);//将链ij划分为A(i) , ( A[i+1:j] )这里实际上就是k=i，s[i][j] = i;for (int k = i + 1; k<j; k++){//将链ij划分为( A[i:k] ),(A[k+1:j])   int u = t[i][k] + t[k + 1][j] + Weight(i - 1, k, j);if (u<t[i][j]){t[i][j] = u;//记录最小的权值s[i][j] = k;//记录划分三角形的顶点，s[i][j]记录了Vi-1和Vj构成最优三角形的第3个顶点的位置}}}
}
return t[1][N - 2];//t[1][5]
}void Traceback(int i, int j, int **s)
{if (i == j) return;Traceback(i, s[i][j], s);//先回溯vi-1,vk的子问题Traceback(s[i][j] + 1, j, s);//再回溯v(k+1),vj的子问题cout << "三角剖分顶点：V" << i - 1 << ",V" << j << ",V" << s[i][j] << endl;
}int Weight(int a, int b, int c)
{	return weight[a][b] + weight[b][c] + weight[a][c];
}