番外12：连续类功率放大器理论-连续类实现带宽拓展的底层原理

连续类功放通解：连续类功率放大器理论-连续类实现带宽拓展的底层原理-基础

本次内容理论性较强，适合对功率放大器理论研究比较感兴趣以及想发论文的小朋友，着重探讨现有的一些带宽拓展模式（也就是连续类）的基本实现原理，并给出其通用的分析求解方法。

1、现有宽带模式概述

1.1 连续F/F-1类

在此主要介绍连续F类，连续F/F-1类PA的归一化电压和电流波形分别如下所示，可以看到连续F类的电流波形与B类PA波形相同，电压波形是在原来的基础上乘以了 $\gamma \sin (\theta ))$ ，在此将 $\gamma \sin (\theta ))$ 成为连续因子。而连续F-1的波形是将连续F类的电压电流交换即可：
$\begin{aligned} &{V_{CF}} = {\left( {1 - \frac{2}{{\sqrt 3 }}\cos \theta } \right)^2} \cdot \left( {1 + \frac{1}{{\sqrt 3 }}\cos \theta } \right) \cdot (1 - \gamma \sin \theta )\\ &{I_{CF}} = \frac{1}{\pi } + \frac{1}{2}\cos \theta + \frac{2}{{3\pi }}\cos (2\theta ) \end{aligned}$
$\begin{aligned} &{V_{CF}} = \frac{1}{\pi } + \frac{1}{2}\cos \theta + \frac{2}{{3\pi }}\cos (2\theta )\\ &{I_{CF}} = {\left( {1 - \frac{2}{{\sqrt 3 }}\cos \theta } \right)^2} \cdot \left( {1 + \frac{1}{{\sqrt 3 }}\cos \theta } \right) \cdot (1 - \gamma \sin \theta ) \end{aligned}$
连续F类波形与连续F-1类波形如下所示：
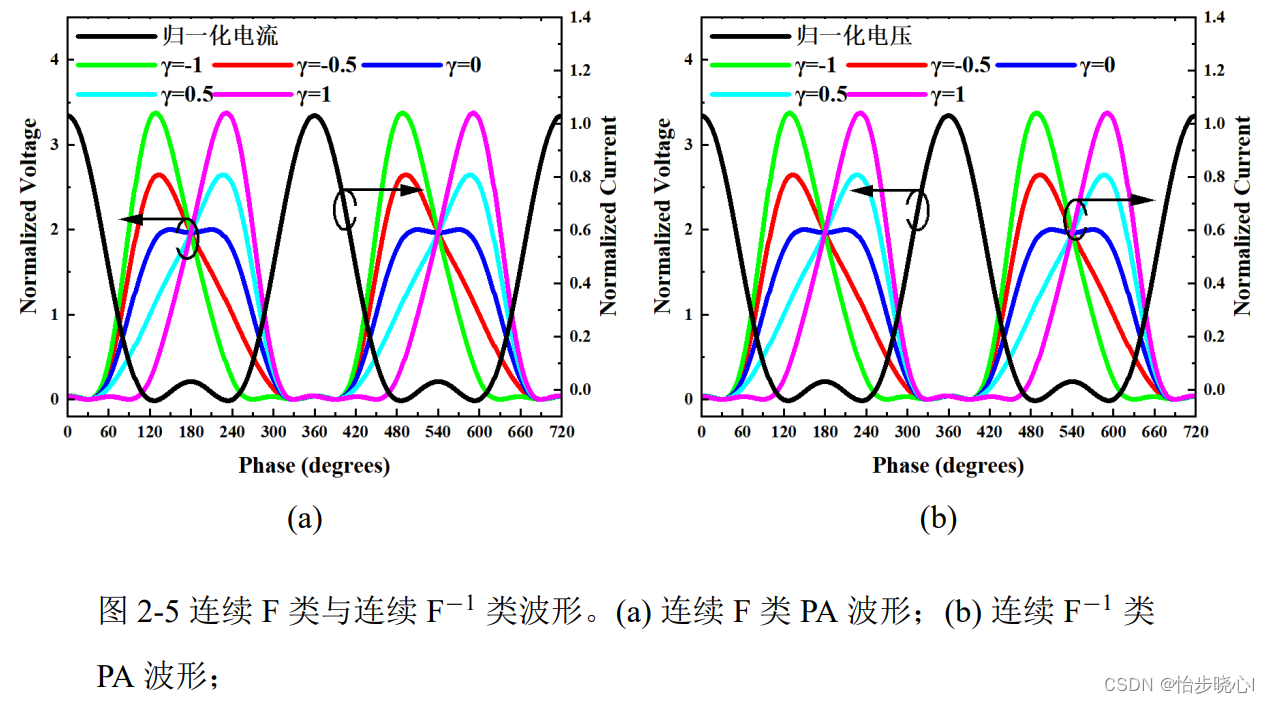
在这里插入图片描述
连续F类与连续 $\rm F^{ - 1}$ 类PA的阻抗空间表达式如下所示：
$\left\{ \begin{aligned} &{Z_{1f,C - F}} = \left( {\frac{2}{{\sqrt 3 }} + j\gamma } \right){R_{opt}}\\ &{Z_{2f,C - F}} = - j\frac{{7\sqrt 3 \pi }}{{24}}{R_{opt}}\\ &{Z_{3f,C - F}} = \infty \end{aligned} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ \begin{aligned} &{Y_{1f,C - {F^{ - 1}}}} = \left( {0.43\sqrt 2 + j0.37\sqrt 2 \gamma } \right){G_{opt}}\\ &{Y_{2f,C - {F^{ - 1}}}} = - j0.98\sqrt 2 \gamma {G_{opt}}\\ &{Y_{3f,C - {F^{ - 1}}}} = \infty \\ &{G_{opt}} = 1/{R_{opt}} \end{aligned} \right.$
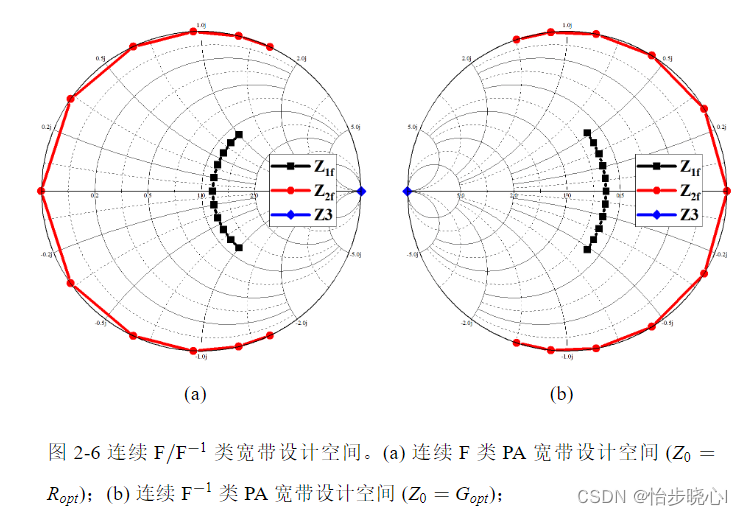
连续F类与连续 $\rm F^{ - 1}$ 类PA的宽带阻抗空间如下图所示：
在这里插入图片描述

！！！！！！！！！！！！！！！！！！TIPS：从波形得到宽带的设计空间！！！！！！！！！！！！！！！

以连续F类为例简要介绍如何从波形得到宽带的设计空间，先将波形定义为傅里叶分解的形式：

$\begin{aligned} & V_{ds}(\theta)=\frac{a_{V, 0}}{2}+\sum_{n=1}^{\infty} a_{V, n} \cos (n \theta)+\sum_{n=1}^{\infty} b_{V, n} \sin (n \theta) \\ & a_{V, 0}=2 \end{aligned}$
$\begin{aligned} & I_{ds}(\theta)=\frac{a_{I, 0}}{2}+\sum_{n=1}^{\infty} a_{I, n} \cos (n \theta)+\sum_{n=1}^{\infty} b_{I, n} \sin (n \theta) \\ & a_{I, 0}=2 \end{aligned}$
将上面的连续F类的波形进行分解与化简，其中电压波形进行了直流归一化，电流波形进行了峰值归一化：
$\begin{aligned} &{V_{CF}} = {\left( {1 - \frac{2}{{\sqrt 3 }}\cos \theta } \right)^2} \cdot \left( {1 + \frac{1}{{\sqrt 3 }}\cos \theta } \right) \cdot (1 - \gamma \sin \theta )\\ &{\rm{ = 1}} - \frac{2}{{\sqrt 3 }}\cos \theta - \gamma \sin \theta {\rm{ + }}\frac{{{\rm{7}}\gamma }}{{{\rm{6}}\sqrt 3 }}\sin {\rm{2}}\theta {\rm{ + }}\frac{{\rm{1}}}{{{\rm{3}}\sqrt 3 }}\cos 3\theta - \frac{{{\rm{7}}\gamma }}{{{\rm{6}}\sqrt 3 }}\cos 4\theta \\ &{I_{CF}} = \frac{1}{\pi } + \frac{1}{2}\cos \theta + \frac{2}{{3\pi }}\cos (2\theta ) \end{aligned}$
阻抗的计算公式如下所示，其实就是电压除以电流，但是使用向量的形式进行计算：
${Z_{nf}} = - \frac{{{a_{Vc,n}}(\beta ) + j{b_{Vc,n}}(\beta )}}{{{a_{I,n}} + j{b_{I,n}}}}$
考虑到：
${R_{opt}} = \frac{{{V_{DD}} - {V_{knee}}}}{{{I_{\max }}/2}}$
忽略膝点电压，带入连续F类的相关傅里叶分量，可得最终表达式（电压波形进行了直流归一化，电流波形进行了峰值归一化）：
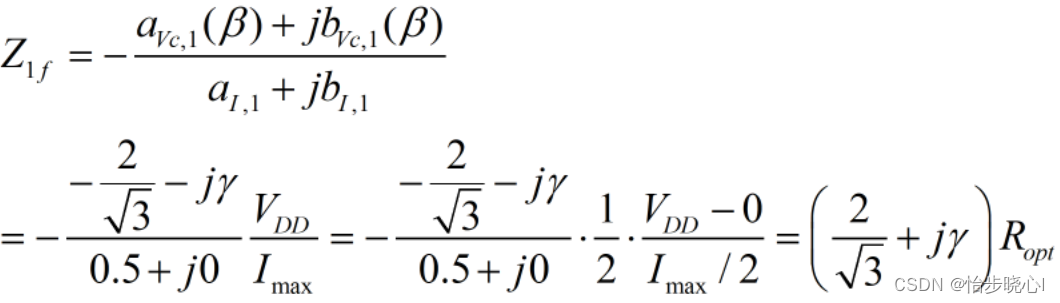
在这里插入图片描述
但是一般在绘制阻抗圆图时，我们也会对这个阻抗取共轭来和实际的设计情况进行匹配（匹配方向问题），因此有些学者画图时都会对这个阻抗取共轭（例如Cripps的连续F类鼻祖论文：The Continuous Class-F Mode Power Amplifier，其中gamma=-1的基波阻抗对应Smith圆图的上半平面，这与一般的公式结果不一致），如下所示（国内许多学者都会忽视这个细节，对于连续F/F-1与连续B/J这种上下对称的阻抗空间还好，对于E类、E/F类、EF类这种如果忽视此细节会直接大乌龙）：
在这里插入图片描述

1.2 连续B/J类

考虑基波和二次谐波时，B类、J类、连续B/J类（C-B/J）PA的时域波形表达式下所示，可以看到连续B/J类的电流波形与B类PA波形相同，电压波形是在原来的基础上乘以了 $\gamma \sin (\theta ))$ ，在此将 $\gamma \sin (\theta ))$ 成为连续因子：
$\begin{aligned} &{I_B}(\theta ) = {I_J}(\theta ) = \frac{1}{\pi } + \frac{1}{2}\cos (\theta ) + \frac{2}{{3\pi }}\cos (2\theta )\\ &{V_B}(\theta ) = (1 - \cos (\theta ))\\ &{V_J}(\theta ) = (1 - \cos (\theta ))(1 - \sin (\theta ))\\ &{V_{C - B/J}}(\theta ) = (1 - \cos (\theta ))(1 - \gamma \sin (\theta )) \end{aligned}$
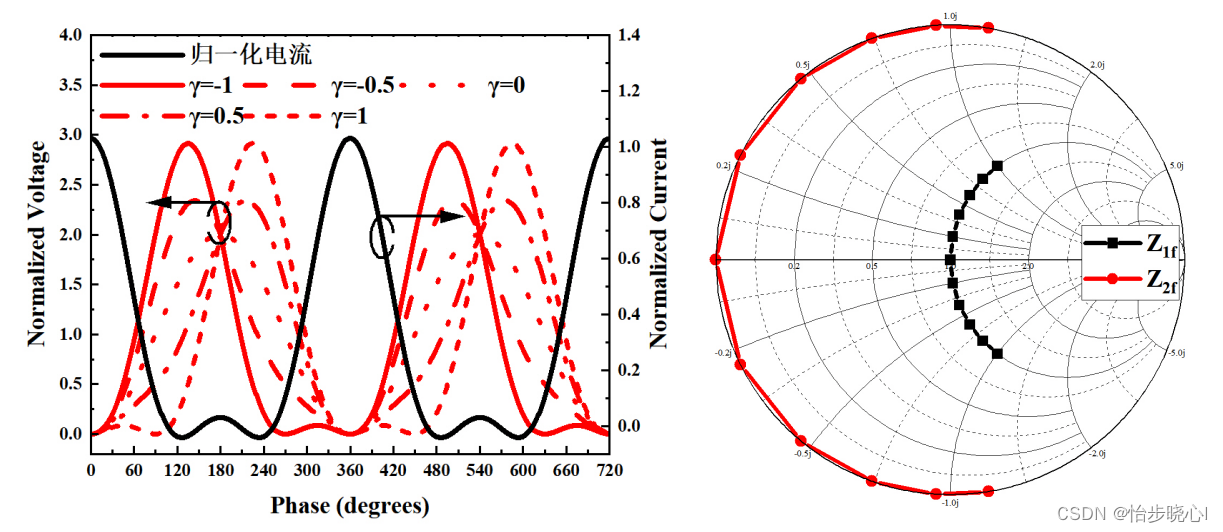
连续B/J类波形与相应的宽带空间如下所示：
在这里插入图片描述

1.3 连续E/E-1类

Almeida, J. V. and K. Wu (2021). “Theory of continuous inverse class‐E power amplifier modes and continuous‐mode self‐distortion.” Microwave and Optical Technology Letters 63(8): 2165-2170.

典型的E类PA需要满足ZVS和ZVDS条件以实现100%效率的能量转化。而对于 $\rm E^{ - 1}$ 类PA，其需要满足ZCS和ZCDS条件以确保其100%效率运行。连续B/J类、连续 ${\rm F/{F^{ - 1}}}$ 类通过乘以连续因子以获得更大的宽带设计自由度，而连续 ${\rm E/{E^{ - 1}}}$ 类取得宽带阻抗空间的方法与上述不同。具体来说，连续E类PA的求解需要先定义二次谐波的可变负载并假设三次及以上谐波开路，在此基础上结合ZVS与ZVDS条件进行推导。求得的连续E类PA具备一簇波形，其工作模式在EF2、E和E/F3中切换，由此拓展了原始设计的空间。
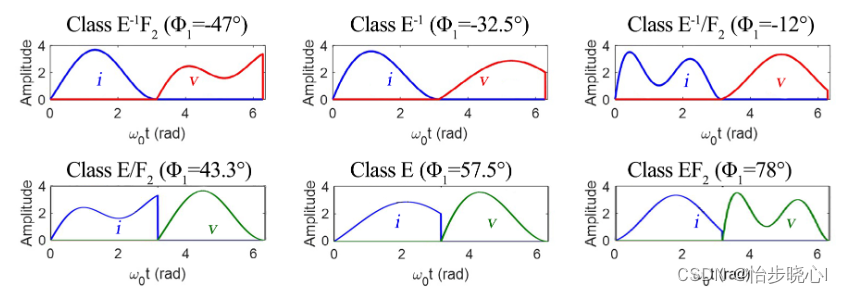
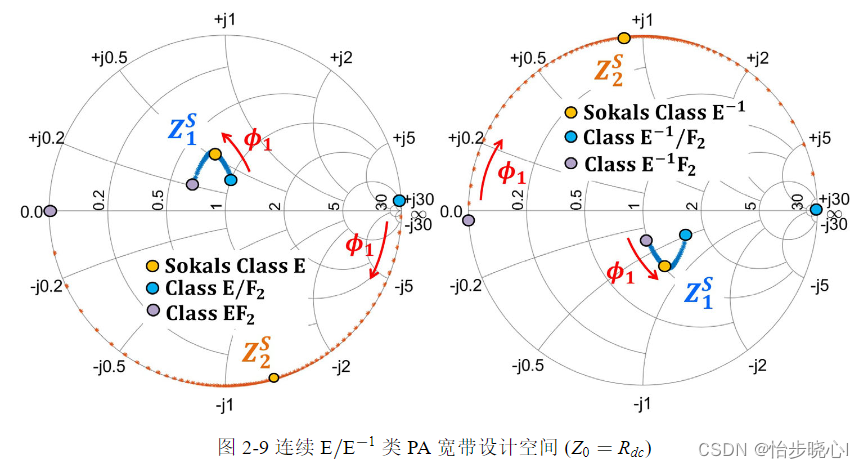
在这里插入图片描述

1.4 带宽拓展的EF与E/F类

Yang, Z., et al. (2020). “A Generalized High-Efficiency Broadband Class-E/F₃ Power Amplifier Based on Design Space Expanding of Load Network.” IEEE Transactions on Microwave Theory and Techniques 68(9): 3732-3744.

Liu, C., et al. (2022). “Novel Design Space of Broadband High-Efficiency Parallel-Circuit Class-EF Power Amplifiers.” IEEE Transactions on Circuits and Systems I: Regular Papers 69(9): 3465-3475.

原始的Class-EF与Class-E/F模式不适用于宽带设计。为解决此问题，有学者在电感 ${L_0}$ 后串联一个可变无功器件 $j X$ ，在此基础上结合ZVS与ZVDS进行波形的求解，由此可以得到一系列随 $X$ 变化的高效率波形并拓展其宽带设计空间。
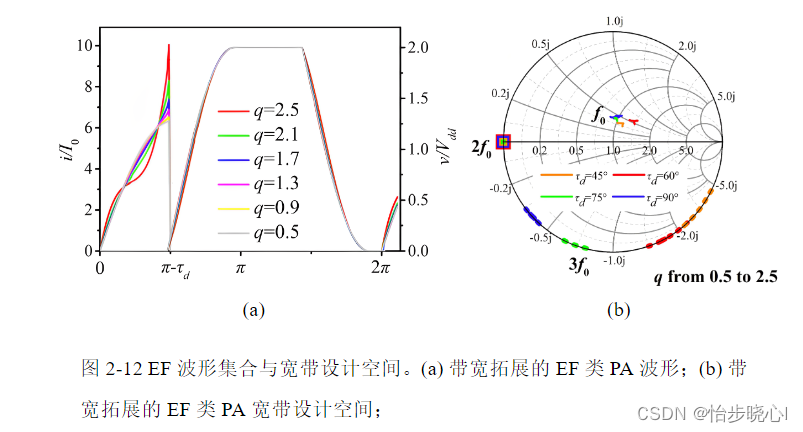
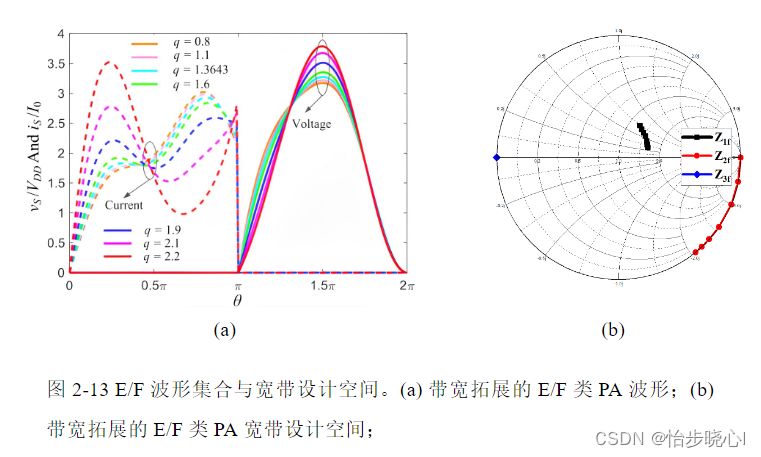
在这里插入图片描述

1.5 带宽拓展的X类

Li, X., et al. (2018). “Class-X—Harmonically Tuned Power Amplifiers With Maximally Flat Waveforms Suitable for Over One-Octave Bandwidth Designs.” IEEE Transactions on Microwave Theory and Techniques 66(4): 1939-1950.

Class-X类PA是一种新兴的谐波调谐PA，此类PA基于最大平坦等理想条件求解出的恒定的输出效率表达式。此外，Class-X类PA的二次谐波和三次谐波阻抗可以独立变化，以最大程度地提供宽带设计空间。经过推导，三次谐波调谐下的X类PA理论效率为75%。其宽带阻抗空间求解需要遵寻一定的流程，此处不详细赘述。
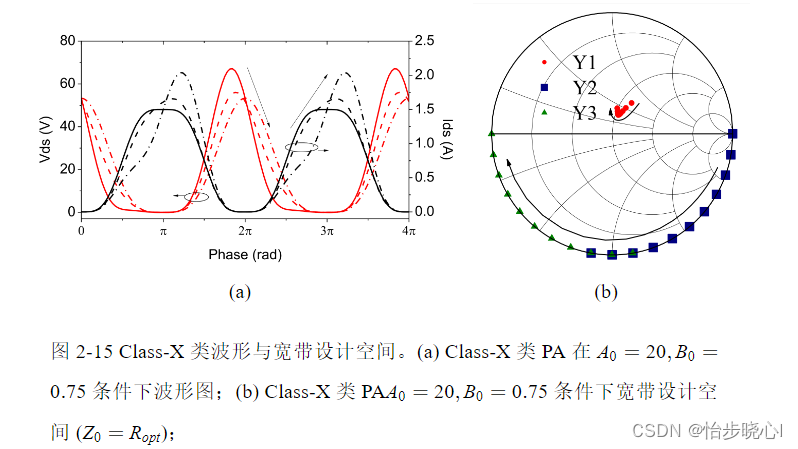
在这里插入图片描述