A - QQ solver (atcoder.jp)直接按题意模拟即可。

B - Caesar Cipher (atcoder.jp)按题意模拟即可

C - Graph Isomorphism (atcoder.jp)按题意模拟即可

D - Weak Takahashi (atcoder.jp) 一个非常套路的网格dp

E - Rook Path (atcoder.jp)

        （1）题意

                有一个H*W的网格，网格中有一个车初始在(x1,y1)这个位置，高桥操作K次后达到(x2,y2)的方案数是多少，每一次移动可以挪到一行或者这一列的任意一个位置上去，但是不能在原始位置。

        （2）思路

                考虑K不大，我们进行O(K)的dp。

                定义dp[i][0]表示前i步操作操作完后和最终位置行列都不同的方案数

                定义dp[i][1]表示前i步操作操作完后和最终位置列相同的方案数

                定义dp[i][2]表示前i步操作操作完后和最终位置列相同的方案数

                定义dp[i][3]表示前i步操作操作完后和最终位置行列都相同的方案数

                1.首先若第i步操作想要变成行列都相同，则前(i - 1)步一定是行相同或者列相同

                        

                2.若第i步操作只要变成行相同，那么前面可能是通过行相同，但第i步走到了不同列，或者是前面i-1步行列都不同走到这行上来了，或者是前面行列都一样，走到不同的列去了。

                        

                3.若第i步操作只要变成列相同，那么前面可能是通过列相同，但第i步走到了不同行，或者是前面i-1步行列都不同走到这列上来了，或者是前面行列都一样，走到不同的行去了。

                        

                4.若第i步操作想要变成行列都不同，那么可能是通过行相同，然后走到了不同行，或者是列相同走到了不同列，或者是行列都不同又走到了行列都不同。

                        

        （3）代码

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
ll dp[N][4];
const ll mod = 998244353;
void solve()
{ll h,w,k;cin >> h >> w >> k;int x1,y1,x2,y2;cin >> x1 >> y1 >> x2 >> y2;if(x1 == x2 && y1 == y2) dp[0][3] = 1;else if(x1 == x2) dp[0][2] = 1;else if(y1 == y2) dp[0][1] = 1;else dp[0][0] = 1;//3 :行列都相同，2：行相同 1：列相同 0：行列都不同rep(i,1,k) {dp[i][3] = dp[i - 1][2] + dp[i - 1][1];dp[i][2] = dp[i - 1][2] * (w - 2) % mod + dp[i - 1][0] + dp[i - 1][3] * (w - 1) % mod;dp[i][1] = dp[i - 1][1] * (h - 2) % mod + dp[i - 1][0] + dp[i - 1][3] * (h - 1) % mod;dp[i][0] = dp[i - 1][2] * (h - 1) % mod + dp[i - 1][1] * (w - 1) + dp[i - 1][0] * (w - 2) % mod + dp[i - 1][0] * (h - 2) % mod;rep(j,0,3) dp[i][j] %= mod;}cout << dp[k][3];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}

F - Simple Operations on Sequence (atcoder.jp)

        （1）题意

                给你一个长度为N的A序列和一个长度为N的B序列，你每次可以对A的一个元素进行加1或减1，这个操作一次花费X元，你也可以对A的一个元素i进行交换，交换A[i]和A[i + 1]，这个操作花费Y元，问你使得A序列变成B序列的最小花费是多少？

        （2）思路

                考虑N不大，我们直接进行状压dp，dp[i]表示i这个点集我已经匹配了多少个A序列的位置，匹配了B的哪些位置需要的最小花费。

                那么考虑转移首先枚举我要放的位置（也就是A未匹配的位置），我们把A[j]这个元素放到z这个位置上去，考虑前面已经放了met个，那么你一定需要交换met次。

                最终输出dp[(1 << N) - 1]即可。

        （3）代码

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 20;
ll dp[1 << N];
int a[N],b[N];
void solve()
{ll n,X,Y;cin >> n >> X >> Y;rep(i,0,n - 1) cin >> a[i];rep(i,0,n - 1) cin >> b[i];memset(dp,0x3f,sizeof(dp));dp[0] = 0;for(int i = 0;i < (1 << n);i ++) {int z = __builtin_popcount(i),met = 0;for(int j = n - 1;j >= 0;j --) {if(!(i >> j & 1)) {dp[i | (1 << j)] = min(dp[i | 1 << j],dp[i] + 1ll * abs(a[j] - b[z]) * X + 1ll * met * Y);}else met ++;}}cout << dp[(1 << n) - 1];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}

G - Modulo Shortest Path (atcoder.jp)

        （1）题意

                给你两个序列A和B，你有一条从i->j的权值为(A[i] + B[j]) % M的边，问你从1走到N的最短路径是多长。

        （2）思路

                考虑暴力，我们建边都要N^2，显然不可行，考虑优化建边。

                对于A序列我们把i向M - A[i]连一条权值为0的边，对于B序列我们把B[i]向i连一条权值为0的边，对于[0,M - 1]把0->1,1->2.....M - 2->M - 1连一条权值为1的边，这样图就变成了这样。

                

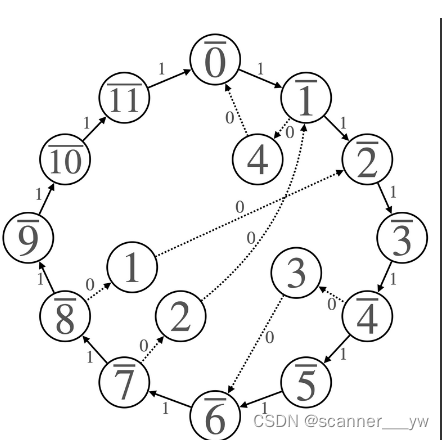
        为什么要向M-A[i]连边而不是向A[i]连边呢？我们考虑分类讨论一下，画一下横坐标就行了。

        好，现在我们的建边从N^2变成了2*N+M,显然M太大过不了，那么考虑其实有些边是用不到的，比如说0-1->2->3->4->5，难道我真要一步步跳过去？显然不可能，我们可以直接压缩成0->5。那哪些模数要用到呢，实际上就是我们建边用的M - a[i]和b[i],从小的向大的连一下即可，然后跑一个最短路就做完了。        

        （3）代码

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 6e5 + 10;
vector<PII> e[N];
int a[N],b[N];
ll dis[N];
vector<int> ver;
int get(int x)
{return lower_bound(all(ver),x) - ver.begin() + 1;
}
inline ll dij(int s,int t)
{memset(dis,0x3f,sizeof(dis));dis[s] = 0;priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>> q;q.push({dis[s],s});while(!q.empty()) {auto [val,u] = q.top();q.pop();for(auto [v,w]: e[u]) {if(dis[v] > val + w) {dis[v] = val + w;q.push({dis[v],v});}}}return dis[t];
}
void solve()
{int n,m;cin >> n >> m;rep(i,1,n) {cin >> a[i];a[i] = (m - a[i]) % m;ver.pb(a[i]);}rep(i,1,n) {cin >> b[i];ver.pb(b[i]);}sort(all(ver));rep(i,1,n) {a[i] = get(a[i]);b[i] = get(b[i]);e[i + sz(ver)].pb({a[i],0});e[b[i]].pb({i + sz(ver),0});}rep(i,1,sz(ver) - 1) {e[i].pb({i + 1,ver[i] - ver[i - 1]});}e[sz(ver)].pb({1,(ver[0] -ver[sz(ver) - 1] + m) % m});cout << dij(1 + sz(ver),n + sz(ver));
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}