C语言之自定义类型_结构体篇（1）

什么是结构？

结构体类型的声明

常规声明

特殊声明-匿名结构体

结构体变量的定义和初始化和访问

定义

初始化

访问

嵌套结构体

结构体的自引用

什么是结构体的自引用

NO1.

NO2.

热门考点：结构体内存对齐

产生内存对齐

NO1

NO2

NO3

内存对齐-结构体类型内存中存储

NO1

NO2

NO3

为什么要对齐

优化结构体成员顺序

修改默认对齐数

百度笔试题

今天来深入结构体，爬了武功山很是艰辛哈哈。

C语言有内置类型：char short int long longlong float double 。但是我们生活中有负责对象需要去描述，例如人需要名字+年龄+身高等等；书需要书名+作者+出版社等等。所以C语言就有了自定义类型：结构体枚举联合体。今天我们重点讲解结构体！

可以先回顾一下结构体的基础知识：C语言之结构体篇_唐唐思的博客-CSDN博客

什么是结构？

结构式一些值的集合，这些值称为成员变量。结构的每个成员可以是不同类型的变量。

可以与数组相比较，数组：一组相同类型元素的集合。

结构体类型的声明

struct tag
{member-list;
}variable-list;

typedef struct 
{member-list;
}tag;

struct 是结构体关键字不能省略
tag 是结构体名字自己命名即可
member-list 是成员列表
variable-list 是结构体类型的变量列表
分号；一定不要忘记
记住结构体是结构体类型，是一种变量类型

常规声明

描述一个学生信息

#include<stdio.h>
struct student
{char name[20];int age;char sex[5];//一个汉字占2个字节+一个\0=5个字节char id[20];//学号
}s1, s2, s3;//分号不能丢
//s1,s2,s3是三个结构体变量，全局变量
int main()
{struct student s5, s6, s7;//ss4,s5,s6是三个结构体变量，局部变量return 0;
}

描述一本书的信息

struct book
{char name[20];char author[12];float printf;
};

结构体类型声明
结构体类型创建变量

特殊声明-匿名结构体

匿名结构体类型是一种特殊结构体类型，只能特殊声明，只能声明一次。

struct
{char name[20];char author[12];float printf;
}b1，b2;
//只能使用一次，也就是b1
//当然如果你想要创建多个结构体类型变量也是可以的

上面的结构体在声明的时候省略了结构体标签（tag)

那么问题来了，可以使用下面这种写法吗？？不建议使用哦

struct
{char name[20];char author[12];float printf;
}b1;struct
{char name[20];char author[12];float printf;
}*p;
int main()
{p = &b1;//不建议这样写，编译器会认为两端的结构体类型不一样
}

警告： 编译器会把上面的两个声明当成完全不同的两个类型。所以是非法的。

结构体变量的定义和初始化和访问

定义

#include<stdio.h>
struct student
{char name[20];int age;
}s1,s2;//定义全局变量struct student s3, s4;//定义全局变量
int main()
{struct student s5, s6;//定义局部变量
}

初始化

#include<stdio.h>
struct student
{char name[20];int age;
}s1 = { "zhangsan",20 };struct student s2 = { "lisi",25 };
int main()
{struct student s3 = { "ruhua",18 };//正序初始化struct student s3 = { .age=18,.name="ruhua"};//乱序初始化
}

访问

#include<stdio.h>
struct student
{char name[20];int age;
};
int main()
{struct student s3 = { "ruhua",18 };//正序初始化struct student s4 = { .age=18,.name="ruhua"};//乱序初始化struct student* s = &s3;printf("%d %s\n", s3.age, s3.name);printf("%d %s\n", (*s).age, (*s).name);printf("%d %s\n", s->age, s->name);
}

嵌套结构体

#include<stdio.h>
struct Point
{int x;int y;
}p1; //声明类型的同时定义变量p1
struct Point p2; //定义结构体变量p2
struct Point p3 = {1,2};//初始化：定义变量的同时赋初值。struct Stu//类型声明
{char name[15];//名字int age;//年龄
};
struct Stu s = { "zhangsan", 20 };//初始化
struct Node
{int data;struct Point p;struct Node* next;
}n1 = { 10, {4,5}, NULL }; //结构体嵌套初始化
struct Node n2 = { 20, {5, 6}, NULL };//结构体嵌套初始化

//嵌套结构体的大小问题
#include<stdio.h>
#include<stddef.h>
struct S3
{double d;char c;int i;
};
struct S4
{char c1;struct S3 s3;double d;
};
int main()
{printf("%d\n", sizeof(struct S4));return 0;
}

结构体的自引用

什么是结构体的自引用

大家应该都听说过数据结构，数据结构就是数据在内存中的存储和组织结构。

这里简单谈一下：假设要将1，2，3，4，5存储在内存中。我们会有怎样的数据结构。

线性数据结构，树形数据结构，图

在线性数据结构中，像1这样一个数据叫节点，如果我们想用结构体去表示一个节点，需要包含哪些信息呢？信息：1.节点本身的信息_数据域 2.找到下一个节点的信息——指针域

那找到下一个节点信息的关键点就是：指针。知道我们知道下一个节点的地址，并且放入上一个节点的结构体成员指针变量中，我们就可以轻松联系节点与节点之间的桥梁。

struct Node
{int data;//本节点信息——数据域struct Node* n;//下一个节点结构体类型的指针变量——指针域
};

typedef struct Node
{int data;//本节点信息——数据域struct Node* n;//下一个节点结构体类型的指针变量——指针域
}Node;

NO1.

问题来了，可以用匿名结构体吗？当然不可以

struct 
{int data;//本节点信息——数据域struct Node* n;//下一个节点结构体类型的指针变量——指针域
};//❌

NO2.

那下面这种写法呢？

typedef struct 
{int data;//本节点信息——数据域Node* n;//下一个节点结构体类型的指针变量——指针域
}Node;//❌

热门考点：结构体内存对齐

我们已经掌握了结构体的基本使用了。现在我们是深入讨论一个问题：计算结构体的大小。

这也是一个特别热门的考点：结构体内存对齐。

产生内存对齐

我们先来看端代码：

#include<stdio.h>
struct S1
{char c1;//1int i;//4char c2;//1
};//6
struct S2
{char c1;//1char c2;//1int i;//4
};//6
int main()
{printf("%d\n", sizeof(struct S1));printf("%d\n", sizeof(struct S2));return 0;
}

为什么不是按照我们预期的内存大小呢？？我们来测试一下每个数据在内存中的偏移量。

【偏移量】偏移量_百度百科 (baidu.com) 通俗来讲就是与起始地址（首地址）的偏移距离

offsetof是宏可以直接使用，用于计算结构体成员相较于起始位置的偏移量

头文件#include<stddef.h>，返回值是偏移量

【宏offsetof】：offsetof - C++ Reference (cplusplus.com)

【宏】我们在后面会讲解。大家可以现在网上了解一下宏，戳一戳：宏（计算机术语）_百度百科 (baidu.com)

NO1

#include<stdio.h>
#include<stddef.h>
struct S1
{char c1;//1int i;//4char c2;//1
};//6
int main()
{printf("%d\n", offsetof(struct S1, c1));printf("%d\n", offsetof(struct S1, i));printf("%d\n", offsetof(struct S1, c2));return 0;
}

我们发现有部分空间是被浪费了的？？那S2也是这样吗？我们来看看

NO2

#include<stdio.h>
#include<stddef.h>
struct S2
{char c1;//1char c2;//1int i;//4
};//6
int main()
{printf("%d\n", offsetof(struct S2,c1));printf("%d\n", offsetof(struct S2,c2));printf("%d\n", offsetof(struct S2, i));return 0;
}

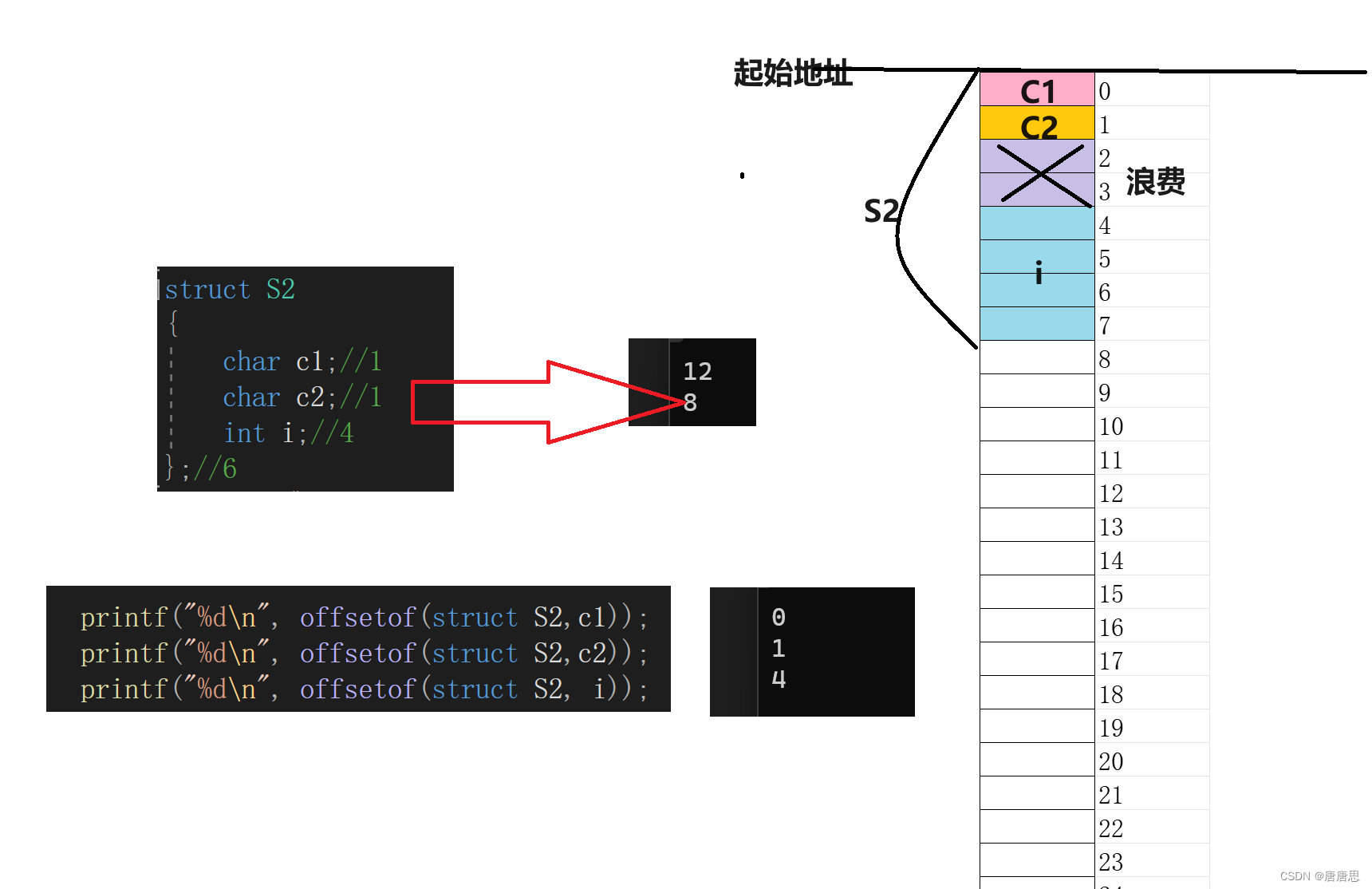
NO3

除了上面的问题我们还有一个嵌套结构体大小的问题哟！🆗🆗

#include<stdio.h>
#include<stddef.h>
struct S3
{double d;char c;int i;
};
struct S4
{char c1;struct S3 s3;double d;
};
int main()
{printf("%d\n", sizeof(struct S4));return 0;
}

关于数据在内存中的存储，偏移量有什么存储规则吗？当然，对齐规则。

内存对齐-结构体类型内存中存储

对齐规则也就是结构体在内存中如何存储

考虑如何计算？那我们首先要掌握结构体的对齐规则：

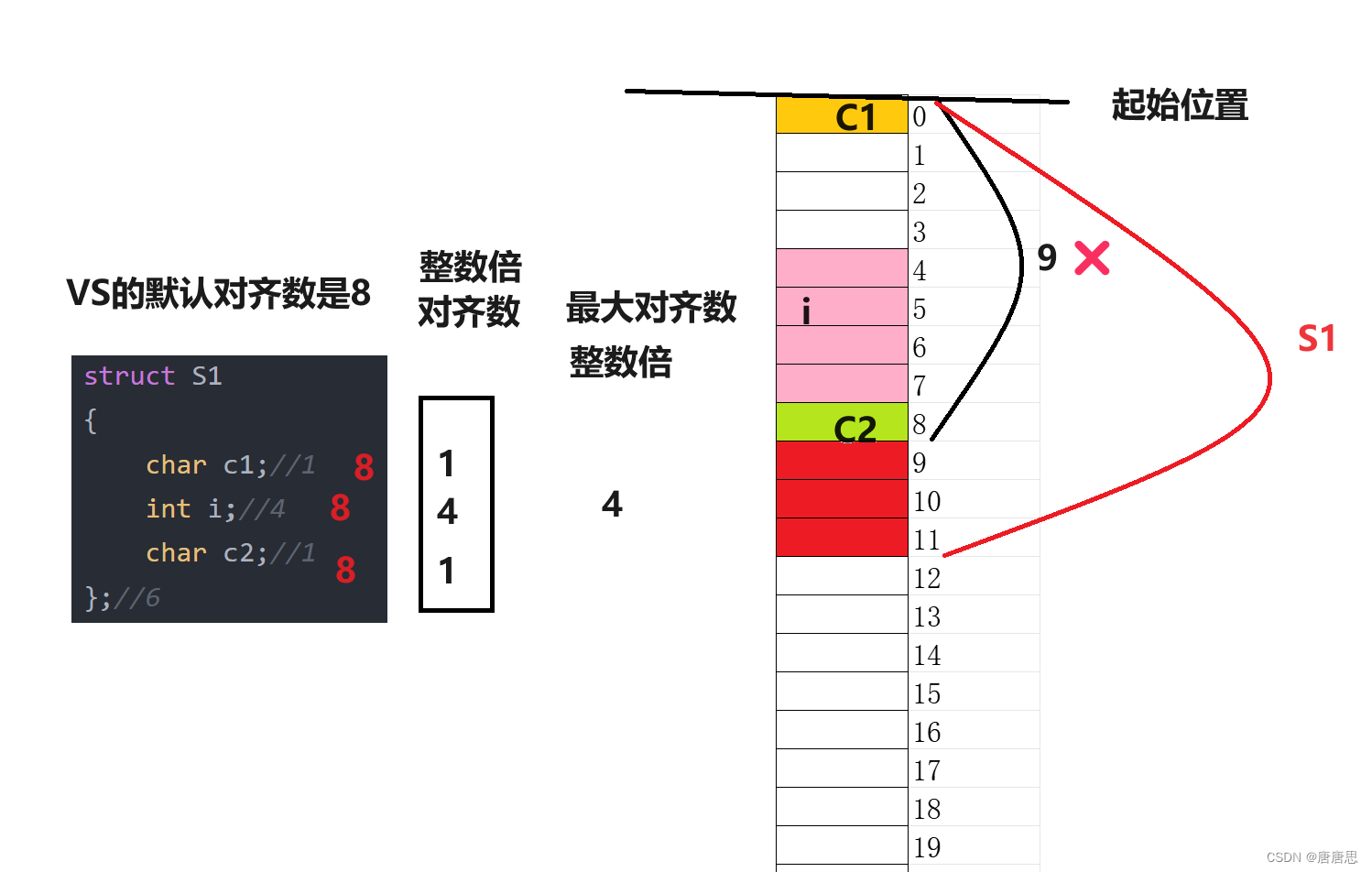
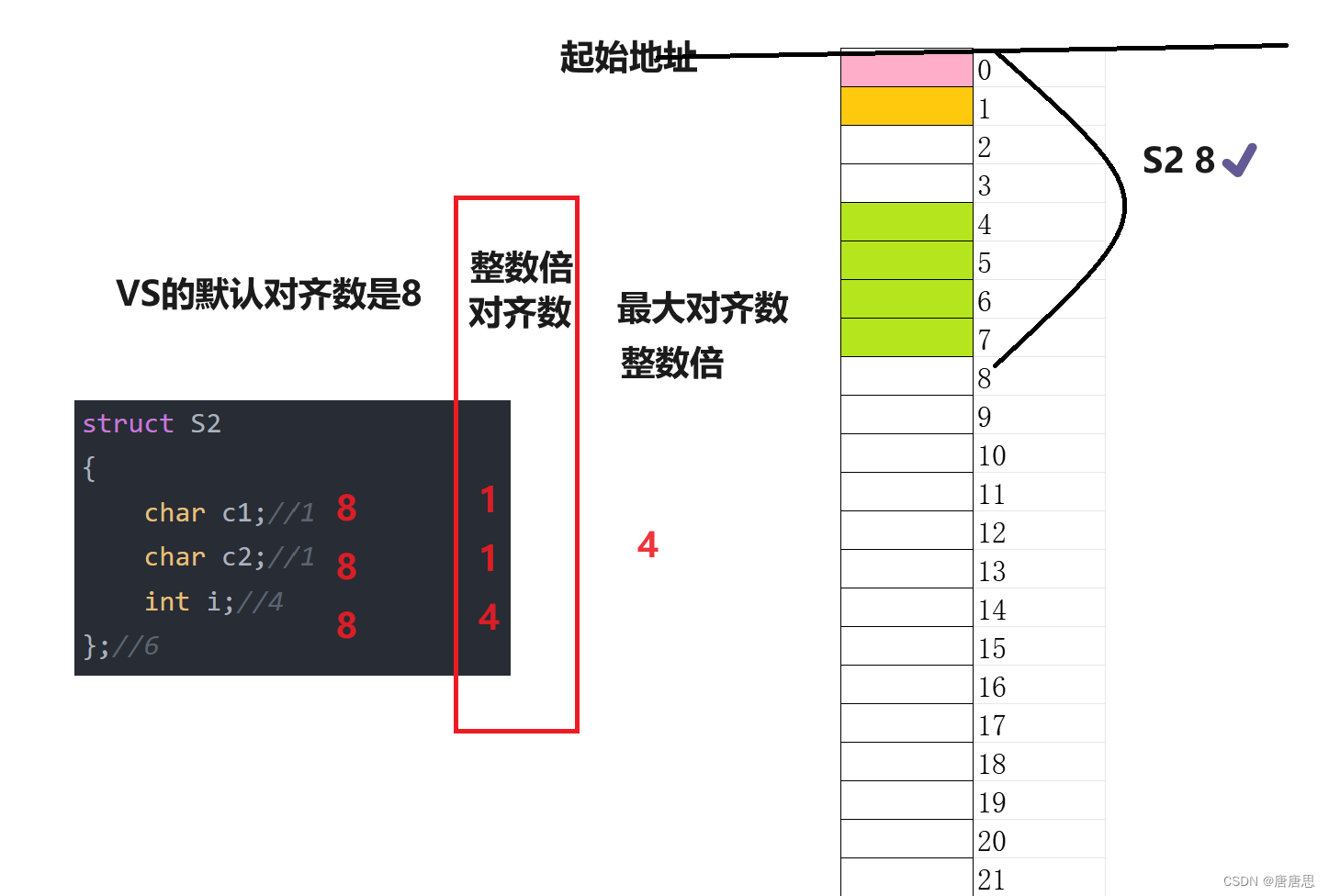
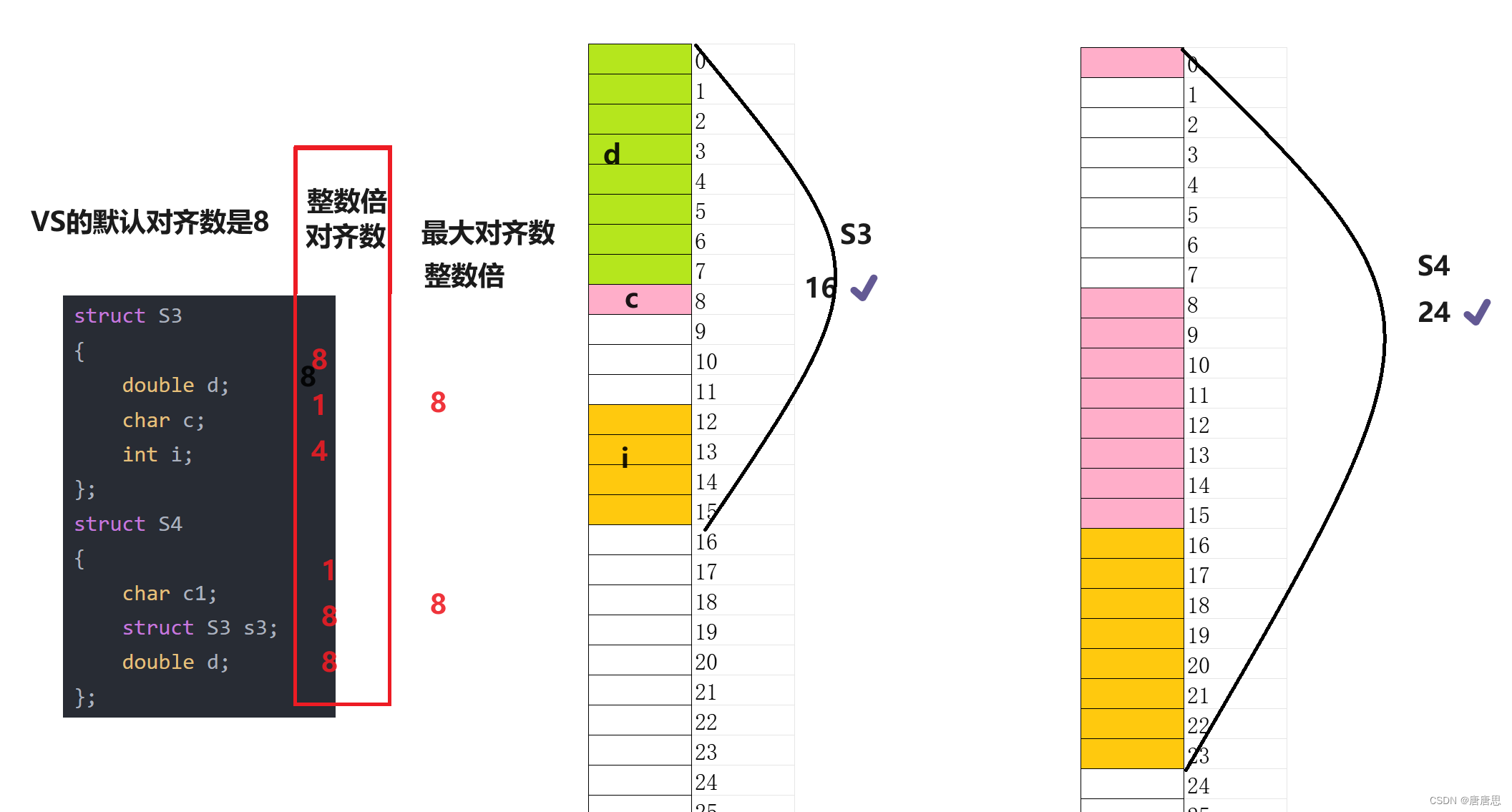
第一个成员在与结构体变量偏移量为0的地址处。
其他成员变量要对齐到某个数字（对齐数）的整数倍的地址处。
结构体总大小为最大对齐数（每个成员变量的对齐数比较之后最大的）的整数倍。
如果嵌套了结构体的情况，嵌套的结构体对齐到自己的成员中对齐数最大对齐数的整数倍处，结构体的整体大小就是所有最大对齐数（含嵌套结构体的对齐数）的整数倍。

对齐数 = 编译器默认的一个对齐数与该成员本省的大小比较之后的较小值。
VS中默认值为8
Linux中gcc没有默认对齐数，对齐数就是成员自身的大小

NO1

#include<stdio.h>
#include<stddef.h>
struct S1
{char c1;//1int i;//4char c2;//1
};//6
int main()
{printf("%d\n", offsetof(struct S1, c1));printf("%d\n", offsetof(struct S1, i));printf("%d\n", offsetof(struct S1, c2));return 0;
}

NO2

#include<stdio.h>
#include<stddef.h>
struct S2
{char c1;//1char c2;//1int i;//4
};//6
int main()
{printf("%d\n", offsetof(struct S2,c1));printf("%d\n", offsetof(struct S2,c2));printf("%d\n", offsetof(struct S2, i));return 0;
}

NO3

#include<stdio.h>
#include<stddef.h>
struct S3
{double d;char c;int i;
};
struct S4
{char c1;struct S3 s3;double d;
};
int main()
{printf("%d\n", sizeof(struct S4));return 0;
}

为什么要对齐

参考大部分资料：

平台原因(移植原因)：不是所有的硬件平台都能访问任意地址上的任意数据的；某些硬件平台只能在某些地址处取某些特定类型的数据，否则抛出硬件异常。
性能原因：数据结构(尤其是栈)应该尽可能地在自然边界上对齐。原因在于，为了访问未对齐的内存，处理器需要作两次内存访问；而对齐的内存访问仅需要一次访问。
总体来说：结构体的内存对齐是拿空间来换取时间的做法

优化结构体成员顺序

那在设计结构体的时候，我们既要对齐，又要节省空间，如何做好：

//例如：
struct S1
{char c1;//1int i;//1char c2;//4
};//8
struct S2
{char c1;//1char c2;//4int i;//1
};//12

S1和S2类型的成员一模一样，但是S1和S2所占空间的大小有了一些区别。

修改默认对齐数

结构在对齐方式不合适的时候，我们可以自己更改默认对齐数。一般设置默认对齐数：2的次方。

#include <stdio.h>
#pragma pack(8)//设置默认对齐数为8
struct S1
{char c1;int i;char c2;
};
#pragma pack()//取消设置的默认对齐数，还原为默认
#pragma pack(1)//设置默认对齐数为1
struct S2
{char c1;int i;char c2;
};
#pragma pack()//取消设置的默认对齐数，还原为默认
int main()
{//输出的结果是什么？printf("%d\n", sizeof(struct S1));printf("%d\n", sizeof(struct S2));return 0;
}

大家自己动一动手画一画图，思考答案！