目录
一、stack
1.1 stack的接口
1.2 关于使用stack的例题
1.2.1 最小栈
1.2.2 栈的压入、弹出序列
1.2.4 逆波兰表达式求值
1.3 stack的模拟实现
二、queue
2.1 queue的接口
2.2 queue的模拟实现
三、deque
3.1 deque底层实现原理
3.1.1 头插实现原理
3.1.2 尾插实现原理
3.1.3 头删、尾删实现原理
3.1.4 在随机位置插入/删除数据实现原理
3.1.5 访问随机位置数据实现原理
3.2 deque的优缺点
3.3 deque迭代器实现原理
一、stack
stack的文档介绍:stack - C++ Reference (cplusplus.com)
 stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,只能从容器的一端进行 元素的插与提取操作(就是数据结构中的栈)。
stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,只能从容器的一端进行 元素的插与提取操作(就是数据结构中的栈)。
stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其底层的容器,并提供一组特定的成员函数来访问其元素,将特定类作为其底层的,元素特定容器的尾部(即栈顶)被压入和弹出。
stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类,这些容器类应该支持这些操作: empty(判空操作)、back(获取尾部元素操作)、push_back(尾部插入元素操作) 、pop_back(尾部删除元素操作)。
标准容器vector、deque、list均符合这些需求,默认情况下,如果没有为stack指定特定的底层容器, 默认情况下使用deque。
1.1 stack的接口
| 函数声明 | 接口说明 |
|---|---|
| stack | 构造空的栈 |
| empty() | 检测stack是否为空 |
| size() | 返回stack中元素的个数 |
| top() | 返回栈顶元素的引用 |
| push(const value_type& val) | 将元素val压入stack中 |
| pop() | 将stack中尾部的元素弹出 |
1.2 关于使用stack的例题
废话不多说:我们直接来使用stack写道题来熟悉熟悉其使用
1.2.1 最小栈
题目地址:
155. 最小栈 - 力扣(LeetCode)
对于该题我们可以建立两个stack,一个stack(_st)用来存储要存储的元素,另一个stack(_min)用来存储前一个stack中最小的元素。在_st入栈时,另一个_min判断入栈的元素是否为_st中所有元素的最小值,如果是就将该元素入栈到_min中,如果不是就将_min中的栈顶元素再次入栈到_min中。当_st出栈时,_min也跟着出栈,这样一来_st和_min的元素始终保持相等,且_min的栈顶元素永远是_st当前状态中的最小元素的值:
class MinStack {
public:MinStack(){}void push(int val) {if(_st.empty()||val<_min.top())_min.push(val);else_min.push(_min.top());_st.push(val);}void pop() {_st.pop();_min.pop();}int top() {return _st.top();}int getMin() {return _min.top();}
private:stack<int> _min;stack<int> _st;
};
但是上述思路中,_min有点浪费空间,我们不必每次_st入栈时都要将_min入栈一个最小元素:如果_st入栈时,入栈的元素大于_st中的最小值,我们可以不用将_min再入栈一个最小元素;在_st出栈时,如果出栈的元素不是_st中的最小值,我们也不必将_min出栈。如此一来,_min的元素始终只保存_st历史入栈时的最小值,且_min的栈顶元素永远是_st当前状态中的最小元素的值:
class MinStack {
public:MinStack(){}void push(int val) {if(_st.empty()||val<=_min.top())_min.push(val);_st.push(val);}void pop() {if(_st.top()==_min.top())_min.pop();_st.pop();}int top() {return _st.top();}int getMin() {return _min.top();}
private:stack<int> _min;stack<int> _st;
};
但是我们还要考虑一个极端情况,如果_st入栈时都是同一个元素呢?我们上面的优化不就不起作用了嘛
对于这种情况,我们可以利用计数的原理再自定义一个类型(Data),这个类型中有两个元素:一个是当前_st中最小元素的值(_val),另一个是记录_st已经连续入栈了多少个这个值(_count)。然后在_min中存储这个类型。
如果_st入栈时,入栈的元素小于_st中的最小值,我们将_min入栈一个Data,这个Data中_val为当前入栈元素,_count置为1;入栈的元素等于_st中的最小值,我们直接将_min的栈顶元素的Data的_count++;入栈的元素大于_st中的最小值,_min不做变化。
在_st出栈时,如果出栈的元素不是_st中的最小值,我们也不必将_min出栈;如果出栈元素是_st中的最小值,我们可以直接将min的栈顶元素的_count--,但如果_count等于1就说明该元素在_st中只剩最后一个了,直接将_min的栈顶元素pop即可。
class Data {
public:Data(int val,int count):_val(val),_count(count){}int _val;int _count;
};class MinStack {
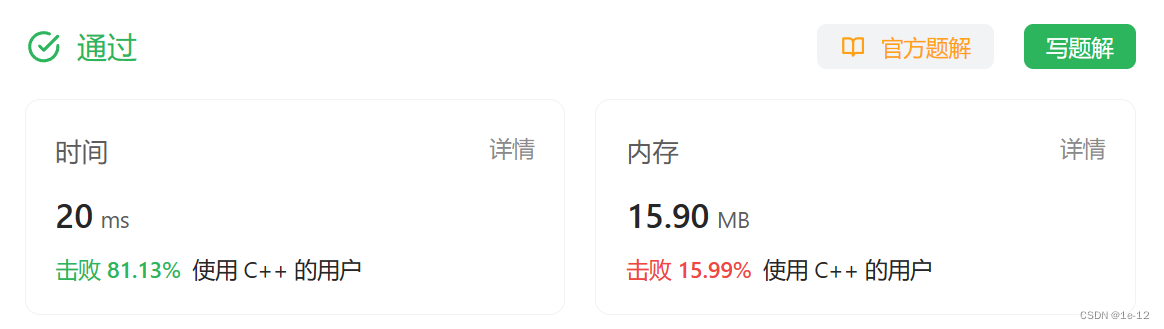
public:MinStack(){}void push(int val) {if (_st.empty() || val < _min.top()._val)_min.push(Data(val, 1));else if (val == _min.top()._val)++_min.top()._count;_st.push(val);}void pop() {if (_st.top() == _min.top()._val){if (_min.top()._count == 1)_min.pop();else--_min.top()._count;}_st.pop();}int top() {return _st.top();}int getMin() {return _min.top()._val;}private:stack<int> _st;stack<Data> _min;
};
1.2.2 栈的压入、弹出序列
题目地址:
栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)
对于这一题我们可以使用一个栈模拟它的出栈和入栈,如果题目所给的出栈和入栈顺序可以匹配的上,最终这个栈就为空。
具体模拟过程为:我们在栈中没有元素的时候按所给的入栈元素顺序,先入一个元素进来,再拿出栈顺序的元素来对比栈顶元素:如果不相等,就继续按入栈顺序再压入一个元素,继续和出栈元素进行匹配;如果相等,就将栈顶元素出栈,拿下一个栈顶元素(如果栈空就压入下一个出栈元素)和下一个出栈的元素进行对比······
以此类推,如果能匹配成功,最终栈为空:
class Solution {
public:bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {size_t num_push=0,num_pop=0;stack<int> _st;_st.push(pushV[num_push++]);for(;num_pop<popV.size();){if(_st.empty() || popV[num_pop]!=_st.top()){_st.push(pushV[num_push++]);}else {_st.pop();++num_pop;}}return _st.empty();}
};
1.2.4 逆波兰表达式求值
题目地址:
150. 逆波兰表达式求值
对于该题我们可以使用一个栈来存储整数,先遍历传入的字符串,如果发现遍历到的字符串是个整数就将该值入栈,如果遍历到的是操作符(+-*/)就拿出栈顶的两个元素进行相对应的运算(运算 时要注意数据的左右所在位置),再将运算结果压入栈中。直到最后栈中的元素就是最终值:
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> val;for(auto& str:tokens)//这里使用&可以减少拷贝{if(str=="+"||str=="-"||str=="*"||str=="/"){ int right=val.top();val.pop();int left=val.top();val.pop();switch(str[0]){case '+':val.push(left+right);break;case '-':val.push(left-right);break;case '*':val.push(left*right);break;case '/':val.push(left/right);break;}}else{val.push(stoi(str));}}return val.top();}
};
1.3 stack的模拟实现
下面我们使用适配器的方式来模拟实现一个stack:
namespace lhs
{template<class T,class container>//container为传入的容器类型class stack{public:void push(const T& val){_st.push_back(val);}void pop(){_st.pop_back();}bool empty(){return _st.empty();}const T& top(){return _st.back();}private:container _st;};
}在这个stack中只要传入一个容器类型container,该容器类型内必须要有push_back()、pop_back()、empty()、back()这几个功能函数,这样我们实现的栈可以直接调用这些函数来实现自己的push()、pop()、empty()、top()功能
下面是使用演示:
int main()
{lhs::stack<int, std::vector<int>> v_st;//顺序栈lhs::stack<int, std::list<int>> l_st;//链式栈for (int i = 0; i < 5; ++i){v_st.push(i);l_st.push(i);}for (int i = 0; i < 5; ++i){std::cout << v_st.top()<<" ";v_st.pop();}std::cout << std::endl;for (int i = 0; i < 5; ++i){std::cout << l_st.top() << " ";l_st.pop();}return 0;
}
但是在STL中stack是不用传容器类型的(STL中stack默认容器类型为deque),我们该怎么办才能做到不声明容器类型呢?
在我们定义模版参数的地方加上一个缺省值即可:
namespace lhs
{template<class T,class container = std::vector<T>>class stack{public:void push(const T& val){_st.push_back(val);}void pop(){_st.pop_back();}bool empty(){return _st.empty();}const T& top(){return _st.back();}private:container _st;};
}模板参数也可以使用缺省值?是的,你没有看错,下面我们来演示其使用:
int main()
{lhs::stack<int> st;for (int i = 0; i < 5; ++i){st.push(i);}for (int i = 0; i < 5; ++i){std::cout << st.top()<<" ";st.pop();}return 0;
}
现在在我们不传容器类型的情况下,该stack使用的容器为vector
二、queue
queue的文档介绍:queue - C++ Reference (cplusplus.com)
queue是一种容器适配器,专门用于在FIFO(先进先出)中操作,其中从容器一端插入元素,另一端 提取元素。
queue作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从队尾入队列,从队头出队列
底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作: empty(检测队列是否为空) size(返回队列中有效元素的个数 )front(返回队头元素的引用) back(返回队尾元素的引用) push_back(在队列尾部入队列) pop_front(在队列头部出队列)
标准容器类deque和list满足了这些要求。默认情况下,如果没有为queue实例化指定容器类,则使用标准容器deque。
2.1 queue的接口
| 函数声明 | 接口说明 |
|---|---|
| queue | 构造空队列 |
| empty() | 检测队列是否为空,是返回true,否则返回false |
| size() | 返回队列中有效元素的个数 |
| front() | 返回队头元素的引用 |
| back() | 返回队尾元素的引用 |
| push() | 在队尾将元素val入队列 |
| pop() | 将队头元素出队列 |
2.2 queue的模拟实现
下面我们继续使用适配器的方式来模拟实现一个queue:
namespace lhs
{template<class T, class container = std::list<T>>class queue{public:size_t size(){return _con.size();}void push(const T& val){_con.push_back(val);}void pop(){_con.pop_front();}bool empty(){return _con.empty();}const T& front(){return _con.front();}const T& back(){return _con.back();}private:container _con;};
}在这里由于queue需要经常进行头删,所以如果使用vector作为其底层适配容器效率是不高的,在这里我们默认queue的底层适配容器为list
测试效果:
int main()
{lhs::queue<int> Q;for (int i = 0; i < 5; ++i){Q.push(i);std::cout << Q.back() << " ";}std::cout << std::endl;std::cout << "size: " << Q.size() << std::endl;while (!Q.empty()){std::cout << Q.front() << " ";Q.pop();}return 0;
}
三、deque
虽然stack和queue中可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器,这是因为stack和队列只是对其他容器的接口进行了包装,STL中stack和queue默认使用deque:deque - C++ Reference (cplusplus.com)


deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比较高。有着vector和list的所有接口:
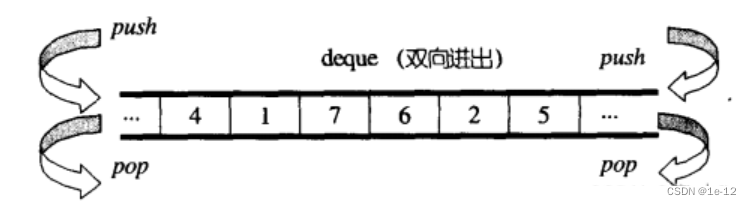
3.1 deque底层实现原理
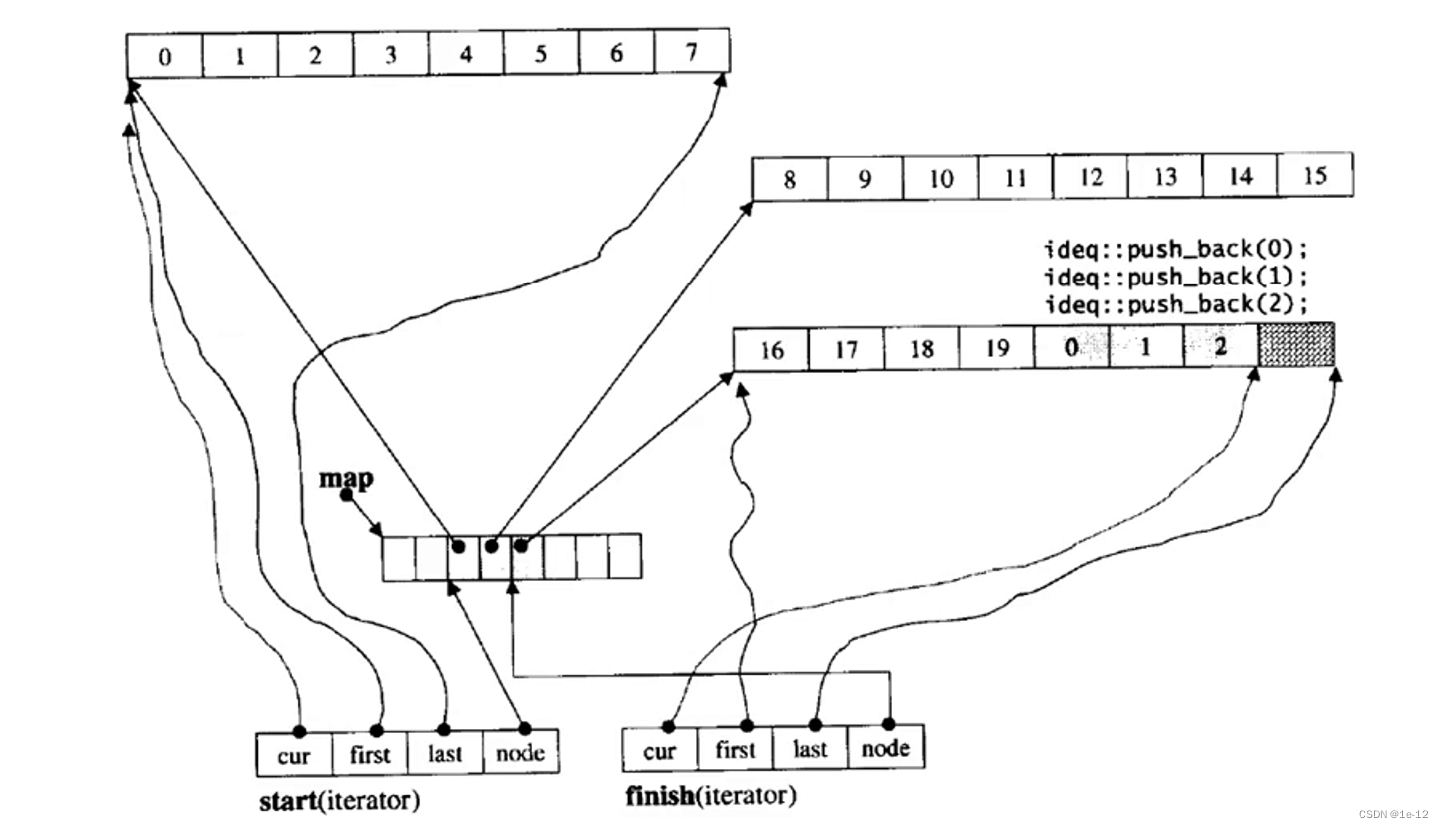
deque为了具有vector和list两者的优势,实现了一种分段存储数据的方法,类似于一个动态的二维 数组,其底层结构如下图所示:
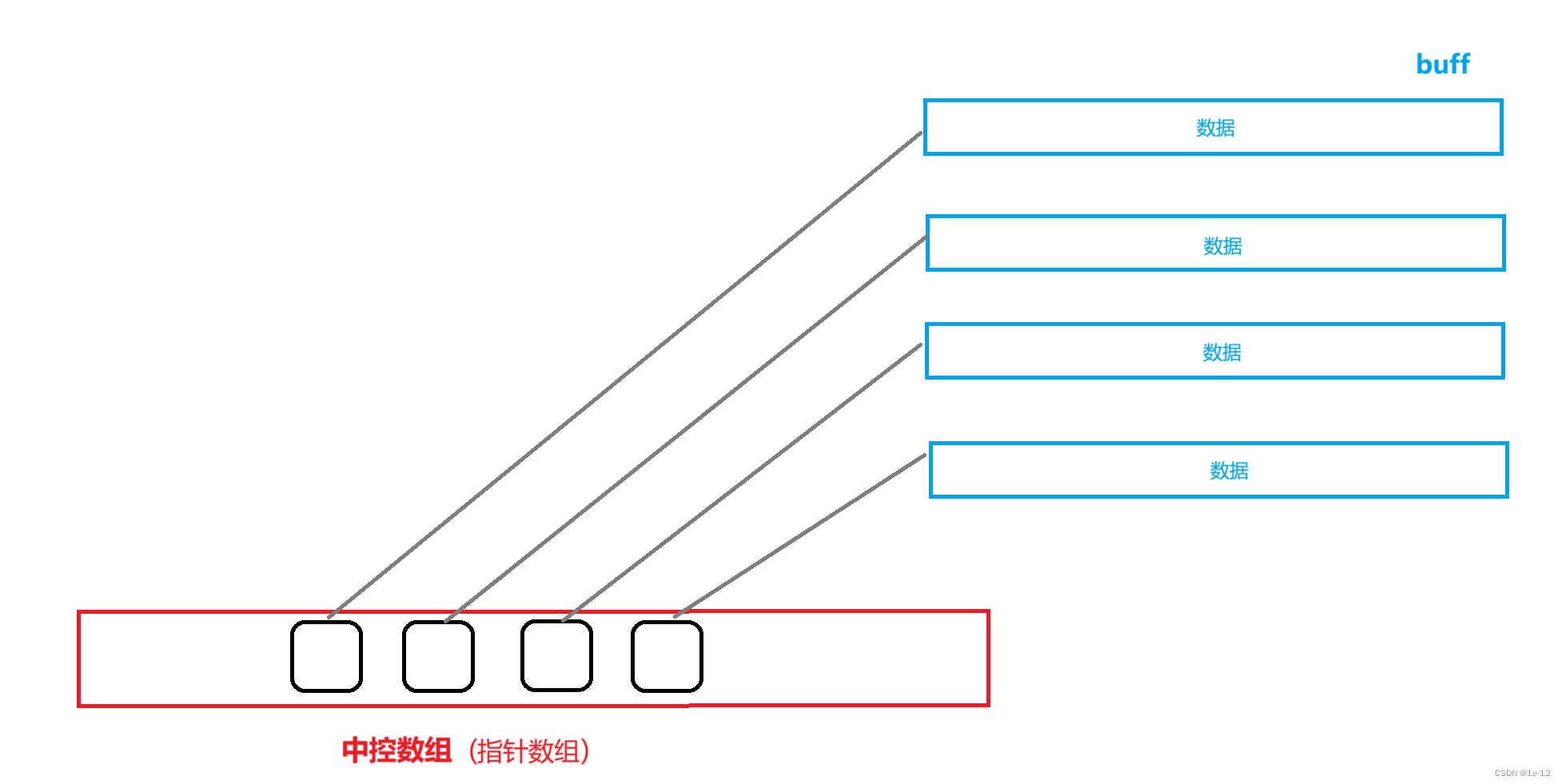
即我们在deque存储的数据存在一个个buff缓冲区中,每一个buff都有一个指针来管理,当存储空间不够时,会再开辟一个buff空间来存储数据,并在中控数组中添加一个指针来管理此区域
3.1.1 头插实现原理
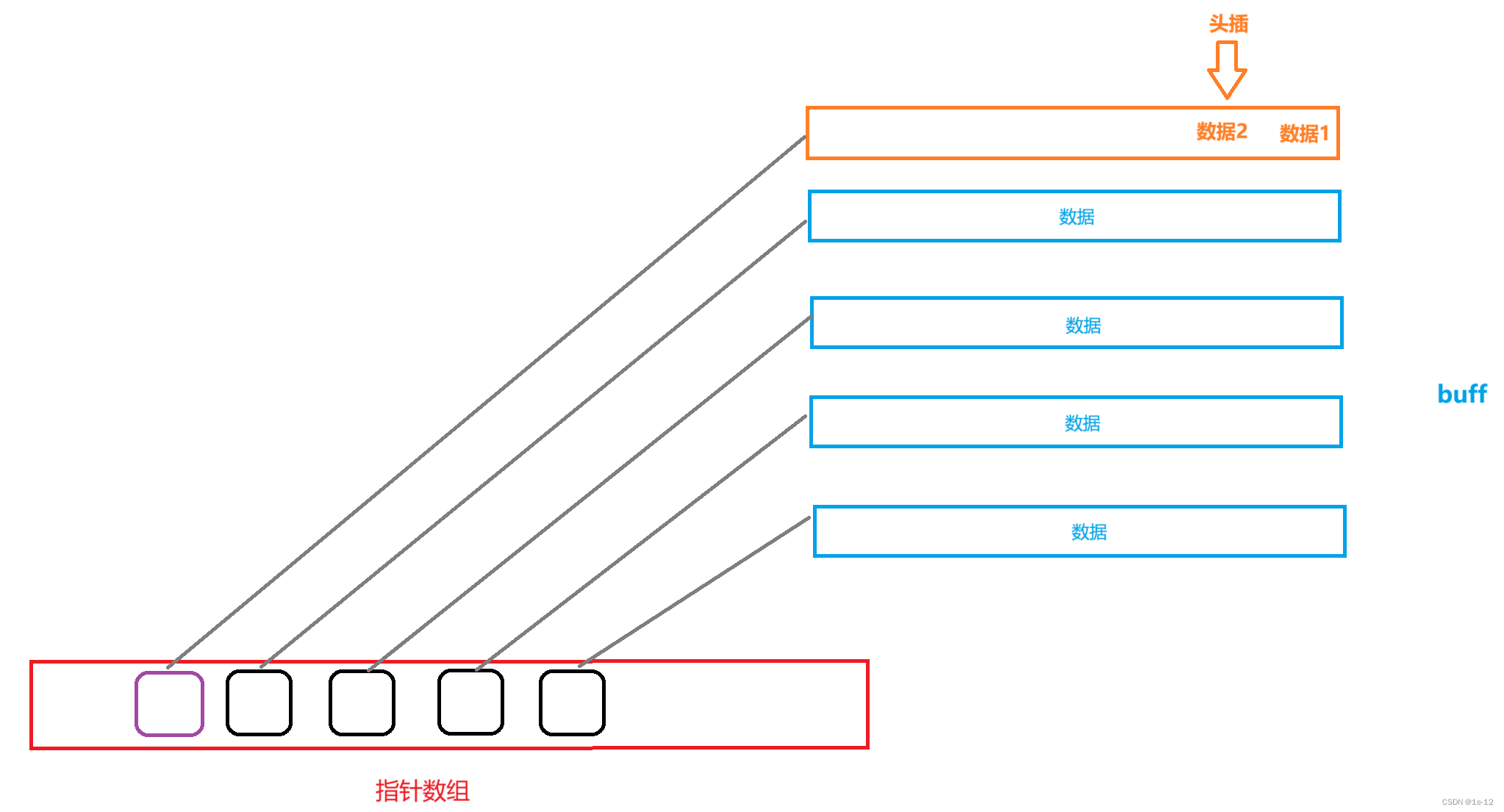
当最前一个buff存满数据时,deque要想实现头插,先要开辟一个buff空间,再在中控数组的最前一个元素前添加一个指针来管理这块空间,最后再将要插入的数据插入到新开辟buff空间的末尾: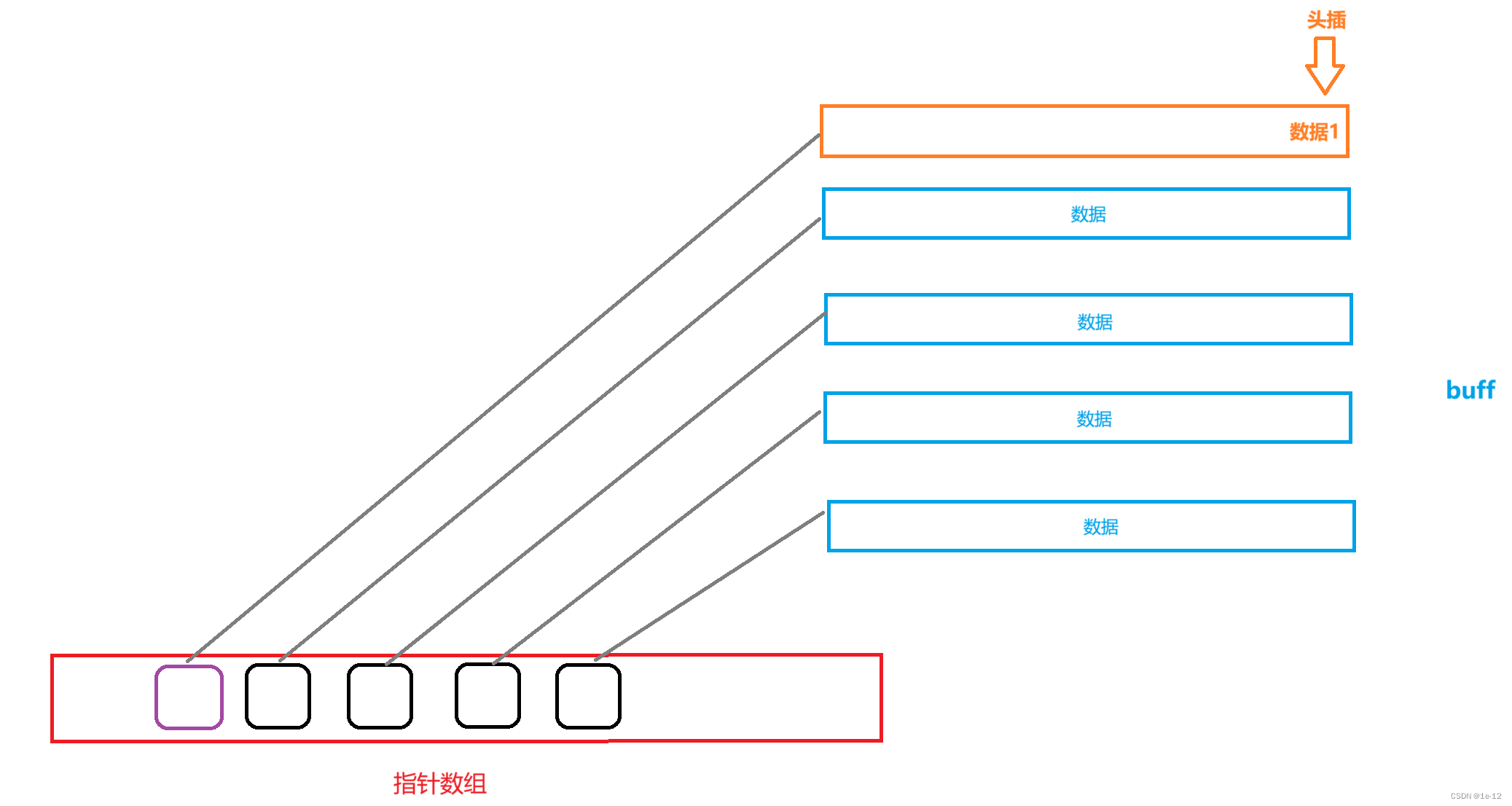
当最前一个buff还没存满数据时,deque要想实现头插,直接将要插入的数据插入到最前一个buff空间的最前一个数据的前面:
3.1.2 尾插实现原理
当最后一个buff存满数据时,deque要想实现尾插,先要开辟一个buff空间,再在中控数组的最后一个元素后添加一个指针来管理这块空间,最后再将要插入的数据插入到新开辟buff空间的开头:
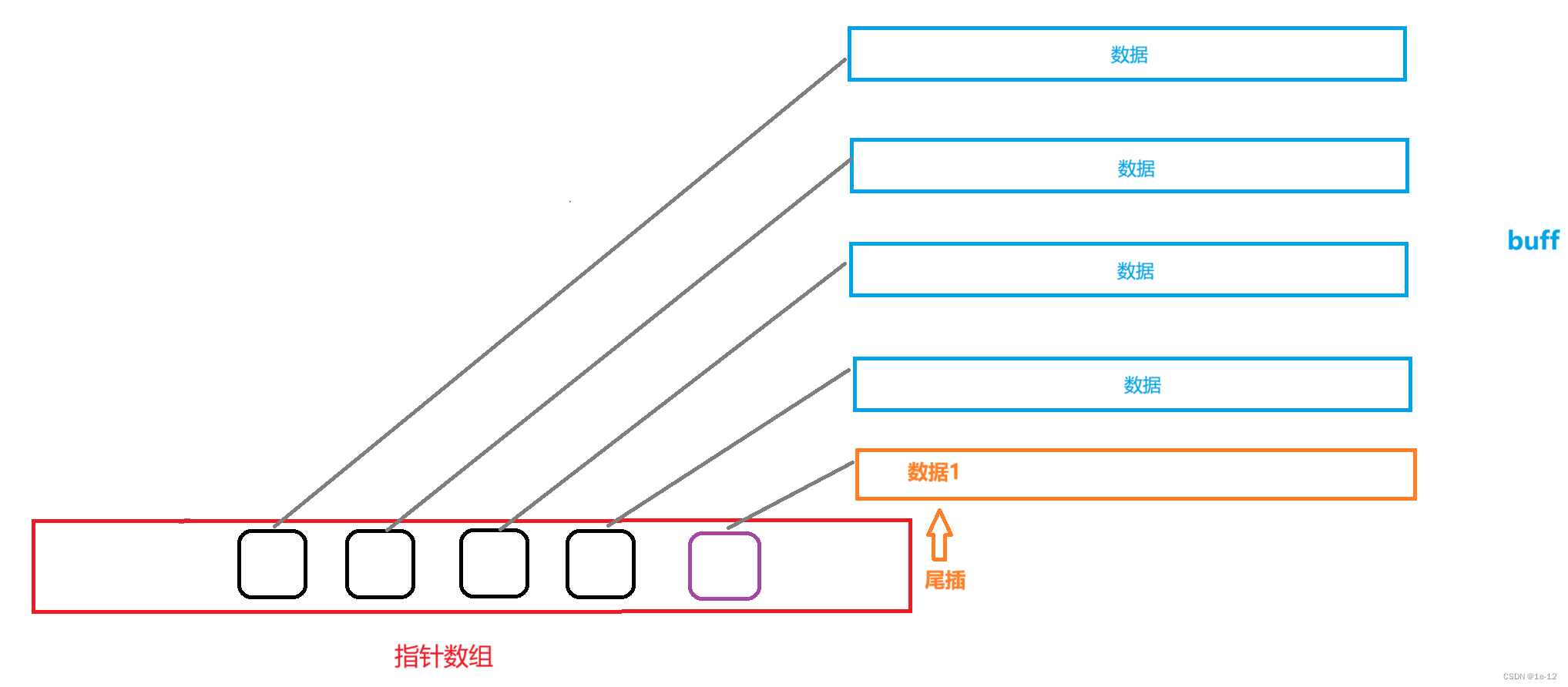
当最后一个buff还没存满数据时,直接将要插入的数据插入到最后一个buff空间的最后一个数据的后面:
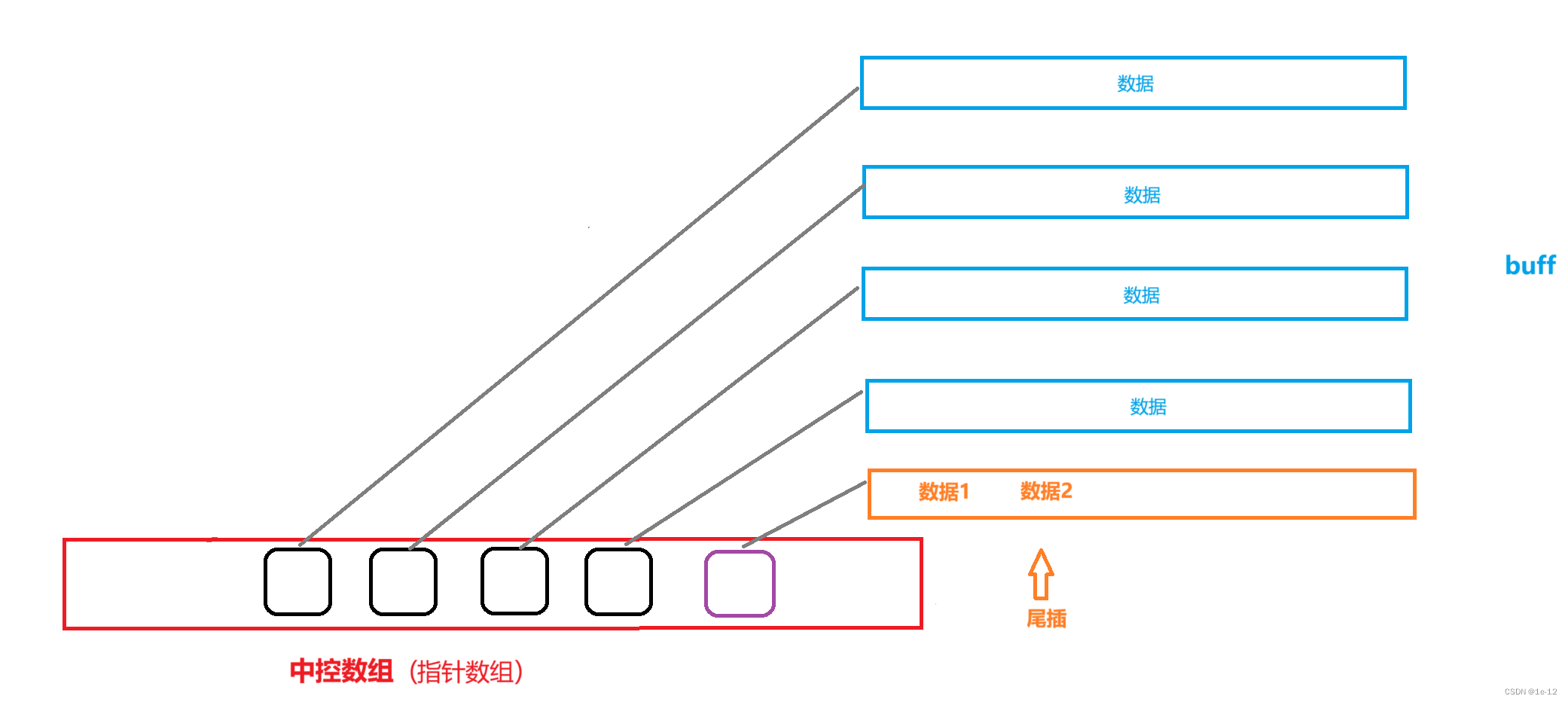
3.1.3 头删、尾删实现原理
deque要头删时会通过指针数组找到第一个buff空间,再删去其空间内的第一个元素,若删完该元素后buff空间无数据,会释放该空间
deque要尾删时会通过指针数组找到最后个buff空间,再删去其空间内的最后一个元素,若删完该元素后buff空间无数据,会释放该空间
这里不再画图演示
3.1.4 在随机位置插入/删除数据实现原理
由于deque的结构,使得在随机位置插入/删除数据变得很麻烦,这里主要有两种思路:
1、在随机位置插入/删除数据时,挪动插入/删除位置后的所有元素的位置(STL中的实现方式)
2、改变插入/删除位置的buff空间大小(此方法虽然效率比上面一种方法快,但会造成buff空间的不一致导致随机访问deque中元素的效率下降)
3.1.5 访问随机位置数据实现原理
如果deque中每个buff空间大小都相等,将想要访问元素的下标减去最前一个buff空间中元素的个数,再除以buff最大所存储数据的个数,即可得到该元素所在的buff空间,最后将想要访问元素的下标模上buff最大所存储数据的个数,即可得到该元素在buff空间的位置
如果deque中每个buff空间大小不相等,只能将想要访问元素的下标一一减去最每一个buff空间中元素的个数,直到为负时就可以确定该元素的位置
3.2 deque的优缺点
了解到其实现原理后,我们可以发现:
与vector比较,deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不需要搬移大量的元素,因此其效率是必vector高的。
与list比较,其底层是连续空间,空间利用率比较高,不需要存储额外字段。
但是,deque的缺陷在于:
不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作 为stack和queue的底层数据结构。
在随机位置插入/删除数据会很麻烦
3.3 deque迭代器实现原理
deque迭代器实现比较复杂:一个指向当前元素的指针cur、一个指向当前buff起始空间地址的指针first、一个指向当前buff结束空间地址的指针last、一个指向当前buff空间的指针node: