T检验是一种统计测试，用于确定两个样本组的均值是否有统计学上的显著差异。以下是对T检验的详细介绍：

定义：

T检验是一种参数检验，它的前提是数据近似于正态分布。它通过计算T统计量，并将其与特定分布（T分布）进行比较，来判断两个样本组的均值之间是否存在显著差异。

主要类型：

单样本T检验：比较一个样本的均值与一个已知或假设的均值。

独立样本T检验（又称为两独立样本T检验）：比较两个独立样本的均值。例如，比较两组人接受不同治疗后的效果。

配对样本T检验（又称为相关样本T检验）：比较同一组人或实体在两个不同时间点或条件下的均值。例如，前后测试中的学生成绩。

前提假设：

数据近似于正态分布。 如果是独立样本T检验，两个样本的方差应该相似（方差齐性）。
数据应为连续数据。
在配对样本T检验中，差异应服从正态分布。

计算：

T统计量的计算公式根据其检验类型略有不同。但基本思路是：差异均值除以差异的标准误差。这给出了样本均值差异相对于期望的随机差异的大小。

解释结果：

结果中会得到一个T值和一个p值。p值告诉我们观察到的数据与零假设（即没有差异）之间的显著性差异。
如果p值小于预定的显著性水平（通常为0.05），则我们拒绝零假设，认为两组之间存在显著差异。
T值的正负号可以告诉我们哪个组的均值较高。

案例

背景：假设我们想要研究一个新的数学教学方法是否对学生的成绩有积极的影响。为此，我们随机选择了两组学生，一组使用传统的教学方法（控制组），另一组使用新的教学方法（实验组）。课程结束后，两组学生都进行了测试。

数据：
控制组（传统方法）的分数：85, 88, 75, 66, 90, 78, 77, 79, 80
实验组（新方法）的分数：92, 95, 90, 85, 97, 91, 88, 90, 93

步骤1：首先，我们需要计算两组的均值。
控制组均值 = 78
实验组均值 = 91.1

步骤2：计算T统计量。这需要更复杂的计算，涉及到两组的方差、样本大小等。但为了简化，我们假设计算后得到T值为3.5。

步骤3：查找T分布表或使用统计软件来确定p值。假设我们得到p值为0.003。

解释：

T值为3.5意味着实验组和控制组之间的均值差异是其标准误差的3.5倍。这是一个相对较大的值，表明两组之间存在显著差异。
p值为0.003远小于常见的显著性水平0.05，这意味着我们观察到的数据在统计学上是显著的。

结论：
基于T检验的结果，我们有足够的证据拒绝零假设（即两种教学方法的效果相同），并认为新的教学方法对学生的数学成绩有积极的影响。

需要注意的是，这个结论只基于我们的样本数据。真实的教育研究会涉及更多的控制变量、更大的样本大小和更复杂的统计方法来确保结论的准确性和可靠性。

上面的只是一个简单的案例，现在我们通过代码来探索实现一个复杂的案例

假设你是一个药物研究者，正在研究一种新的药物对血压的影响。为此，你进行了一个随机、双盲、对照的实验。

你随机选择了50名高血压患者，其中25人接受新药物治疗，另外25人接受安慰剂。实验前后都要测量患者的血压。

任务：

你想要知道新药物是否对血压有显著的降压效果。

import numpy as np
from scipy.stats import ttest_rel# 假设的数据
np.random.seed(42)  # 使得结果可以复现# 生成模拟数据
baseline_bp = np.random.normal(150, 20, 25)  # 基线血压
after_treatment_bp = baseline_bp - np.random.normal(10, 5, 25)  # 治疗后血压# 执行配对样本T检验
t_stat, p_value = ttest_rel(baseline_bp, after_treatment_bp)print("T-statistic:", t_stat)
print("P-value:", p_value)if p_value < 0.05:print("新药物对血压有显著的降压效果。")
else:print("新药物对血压没有显著的降压效果。")

我们使用scipy.stats中的ttest_rel方法，它是专门用于配对样本T检验的。
首先，我们生成了一些模拟数据来表示患者的基线血压和治疗后血压。 然后，我们使用T检验来比较这两组数据。 根据p值，我们可以得出结论。

但是，在实际中，大多数都是多个变量之间对比实验
当涉及到多个变量时，单一的T检验可能不再适用或不足以得出结论。此时，我们需要采用更为复杂的统计方法。以下是几种常见的方法，以及如何处理多个变量的问题：

多重T检验:

当我们对多个组进行比较时，可能会执行多个T检验。但这会增加犯第一类错误（即错误地拒绝了真实的零假设）的风险。
解决办法：Bonferroni 校正是一种简单的方法，将α值（如0.05）除以比较的数量来调整显著性水平。

对于多重T检验，Bonferroni校正是一种控制家族误差率（Familywise Error Rate，FWER）的方法。其基本思想是，当我们进行多次假设检验时，通过降低每次检验的显著性标准（α值），以控制总体上犯第一类错误的风险。

以下是如何实施Bonferroni校正的步骤：

确定原始的α值。通常情况下，α值选择为0.05。
确定你要进行的比较次数，记作m。
调整α值：新的α值为原始α值除以比较次数。即，新的α值 = 原始α / m。
进行每次T检验。
比较每次检验得到的p值与调整后的α值。如果某次检验的p值小于调整后的α值，那么该检验结果被认为是显著的。

示例：

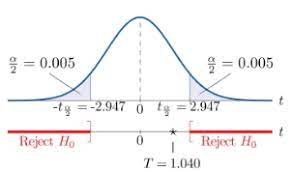
假设你要对5组数据进行两两之间的T检验，那么你总共需要进行10次比较（即5*(5-1)/2 = 10）。如果原始的α值是0.05，那么经过Bonferroni校正后的α值为0.05 / 10 = 0.005。这意味着每次T检验的p值都必须小于0.005，才能被认为是显著的。

Python代码实现：

以下是一个简化的示例，使用Python的scipy.stats库进行多重T检验，并应用Bonferroni校正：

import numpy as np
from scipy.stats import ttest_ind# 假设的数据
np.random.seed(42)group1 = np.random.normal(50, 10, 30)
group2 = np.random.normal(52, 10, 30)
group3 = np.random.normal(55, 10, 30)
group4 = np.random.normal(53, 10, 30)
group5 = np.random.normal(50, 10, 30)groups = [group1, group2, group3, group4, group5]# 计算比较次数
m = len(groups) * (len(groups) - 1) // 2# Bonferroni校正后的α值
alpha_corrected = 0.05 / m# 两两进行T检验
for i in range(len(groups)):for j in range(i+1, len(groups)):t_stat, p_value = ttest_ind(groups[i], groups[j])print(f"Group {i+1} vs Group {j+1}: p-value = {p_value:.4f}")if p_value < alpha_corrected:print(f"显著差异 between Group {i+1} and Group {j+1}")

方差分析（ANOVA）:

当我们想比较三个或更多组的均值时，可以使用一元ANOVA。
如果我们想要同时考虑两个或更多的自变量，可以使用多元ANOVA。
ANOVA的前提是数据应该服从正态分布，且各组的方差应相等（方差齐性）。
协方差分析（ANCOVA）:

ANCOVA允许我们比较多个组的均值，同时控制一个或多个连续的协变量。
这可以帮助我们校正或消除某些变量的影响，从而更清晰地看到其他因子的效果。

1. 基本原理：
   ANOVA分析的基本思想是将数据的总变异分为两部分：组间变异和组内变异。然后根据这两部分的变异来计算一个F统计量，并用其来决定不同组的均值是否相等。

组间变异：反映了不同组之间的差异。
组内变异：反映了同一组内部的差异。

2. 假设：
   零假设（H0）：所有组的均值都相等。
   备择假设（Ha）：至少有两个组的均值不相等。
3. 前提假设：
   数据服从正态分布。
   各组的方差相等，即方差齐性。
   观察值是独立的。
4. 类型：
   一元ANOVA：当我们只有一个分类自变量时使用。
   多元ANOVA（MANOVA）：当我们有两个或更多的分类自变量时使用。
5. 结果解释：
   如果p值小于预定的显著性水平（通常为0.05），那么我们拒绝零假设，认为至少有两个组的均值不相等。
   F统计量的大小表示组间和组内差异的相对大小。较大的F值表示组间差异较大。
6. 注意事项：
   如果ANOVA的结果显著，说明至少有两个组不同，但它不会告诉我们哪些组之间的差异是显著的。为了确定这一点，我们需要进行事后检验，例如Tukey-Kramer方法或Bonferroni校正。
   当数据不满足正态性或方差齐性的假设时，可能需要使用其他非参数方法，如Kruskal-Wallis H检验。
   ANOVA是多个组均值比较的强大工具，但使用时需要确保其前提假设得到满足，并在必要时采取适当的转换或选择替代方法。

当ANOVA的结果显著，意味着我们拒绝了零假设（即所有组的均值相等），但它不告诉我们哪些组之间的差异是显著的。为了确定具体哪些组之间存在显著差异，我们需要进行事后检验（也称为多重比较检验）。

以下是一些常用的事后检验方法：

• Tukey-Kramer方法（Tukey’s Honest Significant Difference, Tukey’s HSD）:

它比较所有组的两两组合。
适用于所有样本大小相等的情况。
它控制了家族误差率，使其保持在显著性水平α之下。

• Bonferroni校正:

这是一个保守的方法，将α值除以比较的数量来调整显著性水平。
例如，如果你有5组数据（进行10次比较），并且α=0.05，则每次比较的显著性水平是0.005。

• Scheffé’s Test:

这是一个非常保守的方法，可以用于任何组合的比较，包括两两比较和多个组的比较。
适用于不平衡设计，即各组的样本大小不等。

• Dunnett’s Test:

当你要将所有其他组与一个特定的控制组进行比较时，Dunnett’s Test是很有用的。
它调整了显著性水平以控制多重比较的误差。

• Newman-Keuls Test:

它进行所有可能的两两比较。
它的特点是步骤化的，即它首先考虑整体差异，然后再进行两两比较。
在Python中进行事后检验：
使用statsmodels库，我们可以进行Tukey-Kramer事后检验

import numpy as np
import statsmodels.api as sm
from statsmodels.stats.multicomp import pairwise_tukeyhsd# 示例数据
data = [83, 85, 84, 76, 88, 92, 95, 89, 90, 78, 83, 86]
groups = ['A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'C', 'C', 'C', 'C']tukey_results = pairwise_tukeyhsd(data, groups, alpha=0.05)print(tukey_results)

这个示例会为’A’, ‘B’, 'C’三组提供两两比较的结果。如果某一对比较的p值小于0.05，那么这两组之间的差异被认为是显著的。

回归分析:

当我们对一个连续的因变量和一个或多个自变量（连续或分类）之间的关系感兴趣时，可以使用回归分析。
线性回归适用于一个连续的因变量和一个或多个连续的自变量。
逻辑回归用于分类的因变量。

混合效应模型:

当我们的数据具有嵌套结构或重复测量时（例如，多次测量同一人），可以使用混合效应模型。
这种模型可以处理固定效应（通常的回归系数）和随机效应（描述数据中的随机变异性）。

主成分分析（PCA）和因子分析:

当我们有大量相关的变量并想要减少维度时，可以使用PCA或因子分析。
这些方法可以帮助我们从多个变量中提取出几个关键组件或因子。
处理多个变量时，关键是选择适合数据结构、研究设计和研究问题的方法。这通常需要对统计方法有深入的理解，并根据数据的特性、分布和假设进行选择。

应用场景：

比如想确定两种不同的训练方法对

学生成绩是否有显著影响；或者是比较男性和女性在某项测试中的表现是否有显著差异等。
T检验是统计学中的基础内容，广泛应用于实验研究和数据分析中，帮助研究者确定观察到的效果是否不仅仅是偶然产生的。

正态性检验:

定义：正态性检验是用来判断一组数据是否近似于正态分布的统计方法。正态分布，也被称为高斯分布，是许多统计技巧和方法背后的关键假设，如t检验、ANOVA和线性回归等。

方法：

图形方法：使用QQ图（Quantile-Quantile Plot）或概率图来视觉判断数据是否遵循正态分布。

统计测试：

Shapiro-Wilk 测试：适用于小样本数据。
Kolmogorov-Smirnov 测试：可以用于任何连续分布，但对正态性检验不如Shapiro-Wilk 测试敏感。
Anderson-Darling 测试：与Kolmogorov-Smirnov类似，但更加权重尾部的差异。
应用场景：在进行如t检验、ANOVA等参数统计分析之前，通常会先进行正态性检验来验证数据的正态分布假设。

一致性检验:

定义：一致性检验是用来判断两个或多个数据集是否来自相同分布的统计方法。这不仅仅局限于正态分布，也可以是其他任何分布。

方法：

Kolmogorov-Smirnov 测试：这是一种非参数方法，用于比较两组独立数据的累积分布函数。
Chi-Square 适合性检验：这是一种检验观察到的频率分布与预期的分布是否有显著差异的方法。
Mann-Whitney U 测试或 Wilcoxon秩和检验：这是一种用于比较两个独立样本是否来自相同分布的非参数方法。
Kruskal-Wallis H 测试：是Mann-Whitney U 测试的扩展，用于三个或更多的独立样本。

应用场景：当你想知道两组或多组数据是否来自同一个总体分布时，可以使用一致性检验。例如，你可能想知道不同处理组的效果是否相同。

总之，这两种检验都是在数据分析中验证数据属性或模型假设的关键步骤，确保你在得出结论或使用特定统计方法时的准确性。

每文一语

每天积累一点