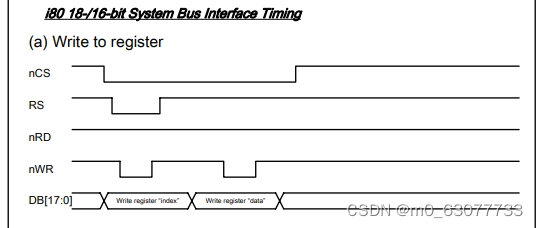
原文:Optimally tackling covariate shift in RKHS-based nonparametric regression. The Annals of Statistics, 51(2), pp.738-761, 2023.
原文作者:Cong Ma, Reese Pathak, Martin J. Wainwright
论文解读者:赵进
编者按:
在再生核希尔伯特空间(RKHS)框架下,本文深入研究了非参数回归的协变量转移问题。特别地,其集中讨论了两类主要的协变量转移问题,它们均由源与目标分布间的似然比所定义。当这些似然比受到均匀上界约束时,文章证明,对于一个具有规范化核特征值的广泛RKHS类,精确调整的正则化参数下的核岭回归(KRR)估计函数是极小极大最优的(仅有对数因子的差异)。值得注意的是,除其上确界外,KRR并不依赖于似然比的完整信息。接下来,针对似然比无上界限制但其第二矩有限的更复杂情况,文章提出了一种基于似然比率的有限截断策略的加权KRR估计方法。并且进一步证实,此估计方法在最小最大意义上达到了最优性,仅存在对数级的差异。
1. 问题背景
1.1 协变量转移下的非参数回归
非参数回归的主旨在于依赖于协变量向量 X ∈ X X\in\mathcal{X} X∈X来预测实数值反应 Y Y Y. 对于每一特定的 x x x, 均方误差最优的估计器由回归函数 f ∗ ( x ) : = E [ Y ∣ X = x ] f^{*}(x):=\mathbb{E}[Y | X = x] f∗(x):=E[Y∣X=x]所描述. 在常规的研究背景中, 我们假设能观察到 n n n个独立同分布的样本对 { ( x i , y i ) } i = 1 n \{(x_{i}, y_{i})\}_{i=1}^{n} {(xi,yi)}i=1n, 其中每个 x i x_{i} xi是按照分布 P P P在 X \mathcal{X} X上抽样得到的,随后 y i y_i yi 是根据条件概率 ( Y ∣ X = x i ) (Y | X=x_i) (Y∣X=xi) 抽样得到的. 我们始终设定, 对于每一个 i i i, 其残差 ω i : = y i − f ∗ ( x i ) \omega_{i} := y_i - f^*(x_i) ωi:=yi−f∗(xi)是具有方差 σ 2 \sigma^2 σ2的次高斯型随机变量.
我们将协变量空间上的分布 P P P称为源分布. 在标准设定中, 估计函数 f ^ \hat{f} f^的性能是根据其 L 2 ( P ) L^2(P) L2(P)误差来衡量的:
∥ f ^ − f ⋆ ∥ P 2 : = E X ∼ P ( f ^ ( X ) − f ⋆ ( X ) ) 2 = ∫ X ( f ^ ( x ) − f ⋆ ( x ) ) 2 p ( x ) d x , \|\hat{f}-f^{\star}\|_P^2 := \mathbb{E}_{X \sim P}(\hat{f}(X)-f^{\star}(X))^2=\int_{\mathcal{X}}(\hat{f}(x)-f^{\star}(x))^2 p(x) d x, ∥f^−f⋆∥P2:=EX∼P(f^(X)−f⋆(X))2=∫X(f^(x)−f⋆(x))2p(x)dx,
其中 p p p是 P P P的密度函数, L 2 ( P ) L^2(P) L2(P)是以 P P P为概率测度的 L 2 L_{2} L2空间.
在协变量转移下, 我们希望构建一个估计函数 f ^ \hat{f} f^, 其 L 2 ( Q ) L^2(Q) L2(Q)误差很小. 在此, 目标分布 Q Q Q与源分布 P P P不同. 从分析角度来看, 设 q q q为 Q Q Q的密度, 我们的目标是找到估计函数 f ^ \hat{f} f^, 使
∥ f ^ − f ⋆ ∥ Q 2 : = E X ∼ Q ( f ^ ( X ) − f ⋆ ( X ) ) 2 = ∫ X ( f ^ ( x ) − f ⋆ ( x ) ) 2 q ( x ) d x \|\hat{f}-f^{\star}\|_Q^2 := \mathbb{E}_{X \sim Q}(\hat{f}(X) - f^{\star}(X))^2 = \int_{\mathcal{X}}(\hat{f}(x) - f^{\star}(x))^2 q(x) d x ∥f^−f⋆∥Q2:=EX∼Q(f^(X)−f⋆(X))2=∫X(f^(x)−f⋆(x))2q(x)dx
尽可能小. 显然,此问题的难度取决于源分布和目标分布之间的某种差异性.
1.2 源-目标似然比上的条件
我们通过似然比来衡量 L 2 ( P ) L^2(P) L2(P)和 L 2 ( Q ) L^2(Q) L2(Q)之间的差异:
ρ ( x ) : = q ( x ) p ( x ) , \rho(x):=\frac{q(x)}{p(x)}, ρ(x):=p(x)q(x),
我们假设对于任意 x ∈ X x\in\mathcal{X} x∈X, ρ ( x ) \rho(x) ρ(x)存在. 通过对似然比施加不同的条件, 我们可以定义不同的源-目标对 ( P , Q ) (P, Q) (P,Q), 我们主要关注两种类型:
均匀 B B B-有界 对于 B ≥ 1 B\geq1 B≥1, 我们称似然比是 B B B-有界的, 如果
sup x ∈ X ρ ( x ) ≤ B , \sup _{x \in \mathcal{X}} \rho(x) \leq B, x∈Xsupρ(x)≤B,
可以看到, B = 1 B=1 B=1表示没有协变量转移的情况, 即 P = Q P=Q P=Q.
χ 2 \chi^2 χ2-有界 实际中, 均匀有界条件往往过于严格, 我们有必要考虑更宽松的条件. 一个放宽的方法是在二阶矩上进行限制. 我们称似然比是 V 2 V^2 V2-时刻有界的, 如果
E X ∼ P [ ρ 2 ( X ) ] ≤ V 2 . \mathbb{E}_{X \sim P}\left[\rho^2(X)\right] \leq V^2 . EX∼P[ρ2(X)]≤V2.
1.3 无权估计与似然加权估计的对比
本文关注基于在再生核定义的希尔伯特空间 H \mathcal{H} H上优化的非参数回归方法。希尔伯特范数 ∥ f ∥ H \|f\|_{\mathcal{H}} ∥f∥H被用作对解决方案施加“平滑性”的手段,无论是通过向目标函数增加一个惩罚项还是通过明确的约束.
在似然比未知的情况下, 一个直接的方法是简单地计算无权的正则化估计值
f ^ λ : = arg min f ∈ H { 1 n ∑ i = 1 n ( f ( x i ) − y i ) 2 + λ ∥ f ∥ H 2 } , \widehat{f}_\lambda := \arg \min _{f \in \mathcal{H}}\left\{\frac{1}{n} \sum_{i=1}^n\left(f\left(x_i\right)-y_i\right)^2+\lambda\|f\|_{\mathcal{H}}^2\right\}, f λ:=argf∈Hmin{n1i=1∑n(f(xi)−yi)2+λ∥f∥H2},
其中, λ > 0 \lambda>0 λ>0是用户定义的正则化参数。当 H \mathcal{H} H是一个再生核希尔伯特空间(RKHS)时,此估计被称为核岭回归(KRR)估计. 这是经验风险最小化的一种形式, 但在协变量转移存在的情境下, 目标涉及对 E P [ ( Y − f ( X ) ) 2 ] \mathbb{E}_{P}[(Y - f(X))^2] EP[(Y−f(X))2] 的经验近似, 而不是 E Q [ ( Y − f ( X ) ) 2 ] \mathbb{E}_{Q}[(Y - f(X))^2] EQ[(Y−f(X))2].
假如似然比已知,那么一个自然的建议是计算似然比加权的正则化估计,
f ~ λ r w : = arg min f ∈ H { 1 n ∑ i = 1 n ρ ( x i ) ( f ( x i ) − y i ) 2 + λ ∥ f ∥ H 2 } . \tilde{f}_\lambda^{\mathrm{rw}}:=\arg \min _{f \in \mathcal{H}}\left\{\frac{1}{n} \sum_{i=1}^n \rho\left(x_i\right)\left(f\left(x_i\right)-y_i\right)^2+\lambda\|f\|_{\mathcal{H}}^2\right\}. f~λrw:=argf∈Hmin{n1i=1∑nρ(xi)(f(xi)−yi)2+λ∥f∥H2}.
引入似然比确保了目标现在提供了对期望值 E Q [ ( Y − f ( X ) ) 2 ] \mathbb{E}_Q\left[(Y-f(X))^2\right] EQ[(Y−f(X))2]的无偏估计. 然而, 通过似然比进行重新加权也增加了方差,尤其是在似然比无界的情况下.
1.4 核函数及其特征值
任何RKHS都与一个半正定核函数 K : X × X → R \mathscr{K}: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R} K:X×X→R 相关. Mercer定理保证该核函数具有以下形式的特征展开
K ( x , x ′ ) = ∑ j = 1 ∞ μ j ϕ j ( x ) ϕ j ( x ′ ) . \mathscr{K}\left(x, x^{\prime}\right) = \sum_{j=1}^{\infty} \mu_j \phi_j(x) \phi_j\left(x^{\prime}\right). K(x,x′)=j=1∑∞μjϕj(x)ϕj(x′).
其中, { μ j } j ≥ 1 \left\{\mu_j\right\}_{j \geq 1} {μj}j≥1为非负特征值序列, 而 { ϕ j } j ≥ 1 \left\{\phi_j\right\}_{j \geq 1} {ϕj}j≥1是在 L 2 ( Q ) L^2(Q) L2(Q)中正交的特征函数.
基于Mercer定理, RKHS范数的平方可以表示为:
∥ f ∥ H 2 = ∑ j = 1 ∞ θ j 2 μ j , θ j = ∫ X f ( x ) ϕ j ( x ) q ( x ) d x . \|f\|_{\mathcal{H}}^2=\sum_{j=1}^{\infty} \frac{\theta_j^2}{\mu_j}, \quad \theta_j=\int_{\mathcal{X}} f(x) \phi_j(x) q(x) d x. ∥f∥H2=j=1∑∞μjθj2,θj=∫Xf(x)ϕj(x)q(x)dx.
因此, 该希尔伯特空间 H \mathcal{H} H可以表示为
H : = { f = ∑ j = 1 ∞ θ j ϕ j ∣ ∑ j = 1 ∞ θ j 2 μ j < ∞ } . \mathcal{H}:=\left\{f=\sum_{j=1}^{\infty} \theta_j \phi_j \mid \sum_{j=1}^{\infty} \frac{\theta_j^2}{\mu_j}<\infty\right\}. H:={f=j=1∑∞θjϕj∣j=1∑∞μjθj2<∞}.
这篇论文的结果要求核函数 κ \kappa κ-均匀有界. 具体来说, 存在一个有限常数 κ > 0 \kappa>0 κ>0, 以下条件成立:
sup x ∈ X K ( x , x ) ≤ κ 2 . \sup _{x \in \mathcal{X}} \mathscr{K}(x, x) \leq \kappa^2. x∈XsupK(x,x)≤κ2.
值得注意的是, 任何在紧致域上连续的核函数自然满足上述条件. 此外, 在实践中广泛使用的许多核,例如高斯核和拉普拉斯核, 都在各自的定义域上满足此条件.
2. 对有界似然比的分析
2.1 无权核岭回归接近最优
在这一节中, 首先推导出在协变量转移下的核岭回归估计函数的一系列上界. 结合之后的分析, 这些界限将证实对于具有有界似然比的协变量转移, KRR估计是仅相差对数项的最小最大优的.
定理1 考虑一个均匀 B B B-有界的似然比, 在一个 κ \kappa κ-均匀有界核的希尔伯特空间上的协变量转移回归问题. 那么, 对于任意的 λ ≥ 10 κ 2 / n \lambda \geq 10 \kappa^2 / n λ≥10κ2/n, 核岭回归估计 f ^ λ \widehat{f}_\lambda f λ 满足以下界限
∥ f λ ^ − f ⋆ ∥ Q 2 ≤ 4 λ B ∥ f ⋆ ∥ H 2 ⏟ b λ 2 ( B ) + 80 σ 2 B log n n ∑ j = 1 ∞ μ j μ j + λ B ⏟ v λ ( B ) , \|\widehat{f_\lambda}-f^{\star}\|_Q^2 \leq \underbrace{4 \lambda B\left\|f^{\star}\right\|_{\mathcal{H}}^2}_{\mathbf{b}_\lambda^2(B)}+\underbrace{80 \sigma^2 B \frac{\log n}{n} \sum_{j=1}^{\infty} \frac{\mu_j}{\mu_j+\lambda B}}_{\mathbf{v}_\lambda(B)}, ∥fλ −f⋆∥Q2≤bλ2(B) 4λB∥f⋆∥H2+vλ(B) 80σ2Bnlognj=1∑∞μj+λBμj,
概率至少为 1 − 28 κ 2 λ e − n λ 16 κ 2 − n − 10 . 1 - 28 \frac{\kappa^2}{\lambda} e^{-\frac{n \lambda}{16 \kappa^2}} - n^{-10}. 1−28λκ2e−16κ2nλ−n−10.
该上界主要包含两项. 首项 b λ 2 ( B ) \mathbf{b}_{\lambda}^2(B) bλ2(B)描述了KRR估计的平方偏差, 此偏差随着正则化参数 λ \lambda λ和似然比界 B B B的增加而成比例增长. 其次, v λ ( B ) \mathbf{v}_{\lambda}(B) vλ(B)刻画了KRR估计器的估计方差, 它在 λ \lambda λ的增长下呈现减小的趋势, 从而暗示 λ \lambda λ在调控偏差与方差之间的平衡中起到了核心作用.
接下来进一步分析导致最优 λ ∗ ( B ) \lambda^{*}(B) λ∗(B)的平衡过程. 对于具有规则特征值的核, 这一过程可以更容易地理解. 对于给定的目标误差 δ > 0 \delta>0 δ>0, 考虑描述第一个低于 δ 2 \delta^2 δ2的特征值的指标 d ( δ ) d(\delta) d(δ), 即 d ( δ ) : = min { j ≥ 1 ∣ μ j ≤ δ 2 } d(\delta) := \min\{j\geq1 | \mu_j\leq\delta^2\} d(δ):=min{j≥1∣μj≤δ2}. 特征值序列被称为正则的,如果
∑ j = d ( δ ) + 1 ∞ μ j ≤ c d ( δ ) δ 2 , \sum_{j=d(\delta)+1}^{\infty} \mu_j \leq c d(\delta) \delta^2, j=d(δ)+1∑∞μj≤cd(δ)δ2,
对某常数 c c c成立. 正则特征值核的包括有限秩核以及特征值在多项式或指数层面上呈现逐渐衰减的核, 这些核广泛应用于实际中. 对于带有正则特征值的核函数, 我们可以证明存在常数 c ′ c' c′使得
∥ f ^ λ − f ⋆ ∥ Q 2 ≤ c ′ { δ 2 ∥ f ⋆ ∥ H 2 + σ 2 B d ( δ ) log n n } , δ 2 = λ B . \|\widehat{f}_\lambda - f^{\star}\|_Q^2 \leq c^{\prime}\left\{\delta^2\left\|f^{\star}\right\|_{\mathcal{H}}^2 + \sigma^2 B \frac{d(\delta) \log n}{n}\right\}, ~~ \delta^2 = \lambda B. ∥f λ−f⋆∥Q2≤c′{δ2∥f⋆∥H2+σ2Bnd(δ)logn}, δ2=λB.
2.2 带有协变量偏移的正则核的下界
上一节我们为非加权的KRR估计建立了上界. 这一节我们证明对于具有正则特征值的核, 非加权KRR估计函数所实现的界是极小极大最优的.
定理2 对于任意的 B ≥ 1 B\geq1 B≥1, 存在一对似然比为 B B B-有界的分布 ( P , Q ) (P, Q) (P,Q), 以及在 L 2 ( Q ) L^2(Q) L2(Q)中的一组正交基 { ϕ j } j ≥ 1 \{\phi_j\}_{j \geq 1} {ϕj}j≥1 使得对于任意的正则核特征值序列 使得对于任意的正则核特征值序列 使得对于任意的正则核特征值序列 { μ j } j ≥ 1 \{\mu_j\}_{j \geq 1} {μj}j≥1, 有
inf f ^ sup f ⋆ ∈ B H ( 1 ) E [ ∥ f ^ − f ⋆ ∥ Q 2 ] ≥ c inf δ > 0 { δ 2 + σ 2 B d ( δ ) n } . \inf _{\widehat{f}} \sup _{f^{\star} \in \mathcal{B}_{\mathcal{H}}(1)} \mathbb{E}[\|\widehat{f}-f^{\star}\|_Q^2] \geq c \inf _{\delta>0}\left\{\delta^2+\sigma^2 B \frac{d(\delta)}{n}\right\}. f inff⋆∈BH(1)supE[∥f −f⋆∥Q2]≥cδ>0inf{δ2+σ2Bnd(δ)}.
与2.1节末的结果相比, 我们观察到当选择合适的正则化参数 λ \lambda λ时, KRR 估计函数实现了极小极大最优 (仅相差对数项).
3. 对无界似然比的分析
到目前为止,我们的分析都基于 B B B-有界的似然比. 但实际上似然比往往是无界的. 以一个简单的单变量例子为证,假设目标分布 Q Q Q是标准正态分布 N ( 0 , 1 ) \mathcal{N}(0,1) N(0,1), 而源分布 P P P为 N ( 0 , 0.9 ) \mathcal{N}(0,0.9) N(0,0.9). 不难发现, 随着 ∣ x ∣ |x| ∣x∣趋于无穷,似然比 ρ ( x ) \rho(x) ρ(x)也趋于无穷。在1.2节中我们提到,用似然加权估计器的一个担忧是它们可能导致方差的大幅膨胀, 特别是乘以可能无界的似然比 ρ ( x ) \rho(x) ρ(x). 因此, 我们考虑将 ρ ( x ) \rho(x) ρ(x)截断: 更具体地说, 对于给定的 τ n > 0 \tau_{n}>0 τn>0, 我们定义截断后的似然比为
ρ τ n ( x ) : = { ρ ( x ) if ρ ( x ) ≤ τ n τ n otherwise \rho_{\tau_n}(x) := \begin{cases}\rho(x) & \text { if } \rho(x) \leq \tau_n \\ \tau_n & \text { otherwise }\end{cases} ρτn(x):={ρ(x)τn if ρ(x)≤τn otherwise
并定义截断加权KRR估计函数:
f ^ λ r w : = arg min f ∈ H { 1 n ∑ i = 1 n ρ τ n ( x i ) ( f ( x i ) − y i ) 2 + λ ∥ f ∥ H 2 } , \widehat{f}_\lambda^{\mathrm{rw}}:=\arg \min _{f \in \mathcal{H}}\left\{\frac{1}{n} \sum_{i=1}^n \rho_{\tau_n}\left(x_i\right)\left(f\left(x_i\right)-y_i\right)^2+\lambda\|f\|_{\mathcal{H}}^2\right\}, f λrw:=argf∈Hmin{n1i=1∑nρτn(xi)(f(xi)−yi)2+λ∥f∥H2},
其中 λ > 0 \lambda>0 λ>0和 τ n \tau_n τn待定.
在核的特征函数均匀有界时, 我们对估计函数进行了分析. 核特征函数均匀有界指
∥ ϕ j ∥ ∞ : = sup x ∈ X ∣ ϕ j ( x ) ∣ ≤ 1 ∀ j = 1 , 2 , … \left\|\phi_j\right\|_{\infty}:=\sup _{x \in \mathcal{X}}\left|\phi_j(x)\right| \leq 1 \quad \forall j=1,2, \ldots ∥ϕj∥∞:=x∈Xsup∣ϕj(x)∣≤1∀j=1,2,…
关于截断加权KRR估计函数的定理涉及核复杂性函数 Ψ ( δ , μ ) = ∑ j = 1 ∞ min { δ 2 , μ j ∥ f ⋆ ∥ H 2 } \Psi(\delta, \mu)=\sum_{j=1}^{\infty} \min \left\{\delta^2, \mu_j\left\|f^{\star}\right\|_{\mathcal{H}}^2\right\} Ψ(δ,μ)=∑j=1∞min{δ2,μj∥f⋆∥H2}, 并适用于任意满足不等式 M ( δ ) < δ 2 2 \mathcal{M}(\delta)<\frac{\delta^2}{2} M(δ)<2δ2 的解 δ n > 0 \delta_n>0 δn>0, 其中:
M ( δ ) : = c 0 σ 2 V 2 log 3 ( n ) n Ψ ( δ , μ ) . \mathcal{M}(\delta):=c_0 \sqrt{\frac{\sigma^2 V^2 \log ^3(n)}{n} \Psi(\delta, \mu)} . M(δ):=c0nσ2V2log3(n)Ψ(δ,μ).
定理3 考虑均匀有界的特征函数的核, 以及满足 E P [ ρ ( x ) 2 ] ≤ V 2 \mathbb{E}_{P}[\rho(x)^2]\leq V^2 EP[ρ(x)2]≤V2的源-目标分布. 进一步假设噪声的方差满足 σ 2 ≤ κ 2 ∥ f ⋆ ∥ H 2 \sigma^2\leq\kappa^2\|f^{\star}\|_{\mathcal{H}}^2 σ2≤κ2∥f⋆∥H2. 那么, 有截断阈值 τ n = n V 2 \tau_n=\sqrt{nV^2} τn=nV2 和正则化参数 λ ∥ f ⋆ ∥ H 2 ≥ δ n 2 / 3 \lambda\left\|f^{\star}\right\|_{\mathcal{H}}^2\geq\delta_n^2 / 3 λ∥f⋆∥H2≥δn2/3的估计函数 f ^ λ r w \hat{f}_{\lambda}^{rw} f^λrw 有上界:
∥ f ^ λ r w − f ⋆ ∥ Q 2 ≤ δ n 2 + 3 λ ∥ f ⋆ ∥ H 2 , \|\hat{f}_\lambda^{\mathrm{rw}}-f^{\star}\|_Q^2 \leq \delta_n^2+3 \lambda\left\|f^{\star}\right\|_{\mathcal{H}}^2, ∥f^λrw−f⋆∥Q2≤δn2+3λ∥f⋆∥H2,
其概率为 1 − n − 10 1-n^{-10} 1−n−10.
参考文献
[1] Cong Ma, Reese Pathak, Martin J. Wainwright “Optimally tackling covariate shift in RKHS-based nonparametric regression,” The Annals of Statistics, Ann. Statist. 51(2), 738-761, (April 2023)
![Flask框架配置celery-[1]:flask工厂模式集成使用celery,可在异步任务中使用flask应用上下文,即拿即用,无需更多配置](https://img-blog.csdnimg.cn/92a5319c10354348b1c7ba2819c89045.png)