暴力递归到动态规划(一)
- 斐波那契数列的动态规划
- 机器人走路
- 初级递归
- 初级动态规划
- 动态规划
- 先后选牌问题
- 初级递归
- 初级动态规划
- 动态规划
我们可以一句话总结下动态规划
动态规划本质是一种以空间换时间的行为 如果你发现有重复调用的过程 在经过一次之后把结果记下来 下次调用的时候直接用 这就是动态规划
斐波那契数列的动态规划
一般来说我们可以使用递归来解决斐波那契数列问题 代码如下
int fib(int n)
{ if (n <= 0) { cerr << "error" << endl; } if (n <= 2) { return 1; } return fib(n-1) + fib(n-2);
}
当然 这种方式会产生大量的重复计算 所以说我们可以保存上个和上上个的计算值来进行动态规划
int dpfib(int n)
{ if (n <= 2) { return 1; } int i = 1; int j = 1; int k = 0; while (n-2) { k = i + j; i = j; j = k; n--; } return k;
}
这样子写代码就能避免大量的重复计算了
机器人走路
初级递归
假设现在有1~N个位置
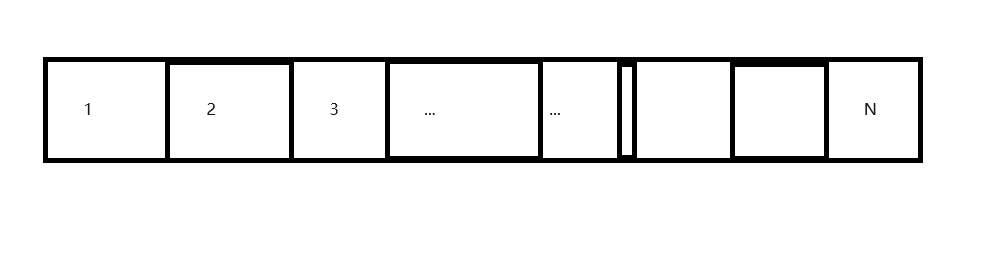
有一个小机器人 现在在START位置
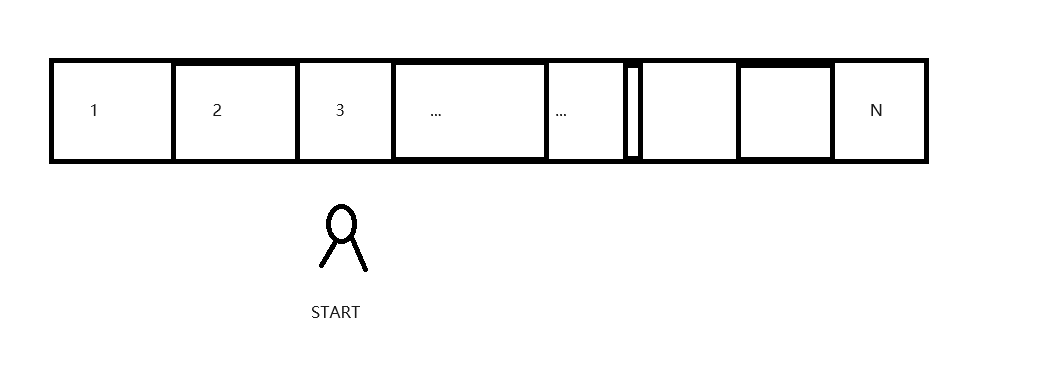
它现在要去aim位置 (aim为1~N上的随机一点) 能走K步 (K >= 0)
每次只能走一步 不能越界 不能停止 现在请问有多少种方式能走走到
现在假设 S = 2 N = 5 AIM = 4 K = 6
我们一开始写出的递归方程如下
int process1(int cur , int rest , int aim , int k)
参数含义如下
- cur 当前位置
- rest 剩余步数
- aim 目标地点
- k 能走的步数
base case为
- 如果剩余步数为0 则判断cur是否为aim地点
否则我们执行递归继续往下走
int process1(int cur , int rest , int aim , int n)
{ if (rest == 0){return cur == aim ? 1 : 0;}if (cur == 1){return process1(2 , rest -1 , aim , n);}if (cur == n){return process1(n-1 , rest-1 , aim , n);} return process1(cur-1 , rest-1 , aim , n)+ process1(cur+1 , rest-1 , aim , n);
}
初级动态规划
现在我们要进行进一步的动态规划
我们想想看在递归函数中有真正决定的是哪两个参数
我们每次传递参数的时候 aim 和 n 是不变的
其实每次变化的就是 cur 和 rest
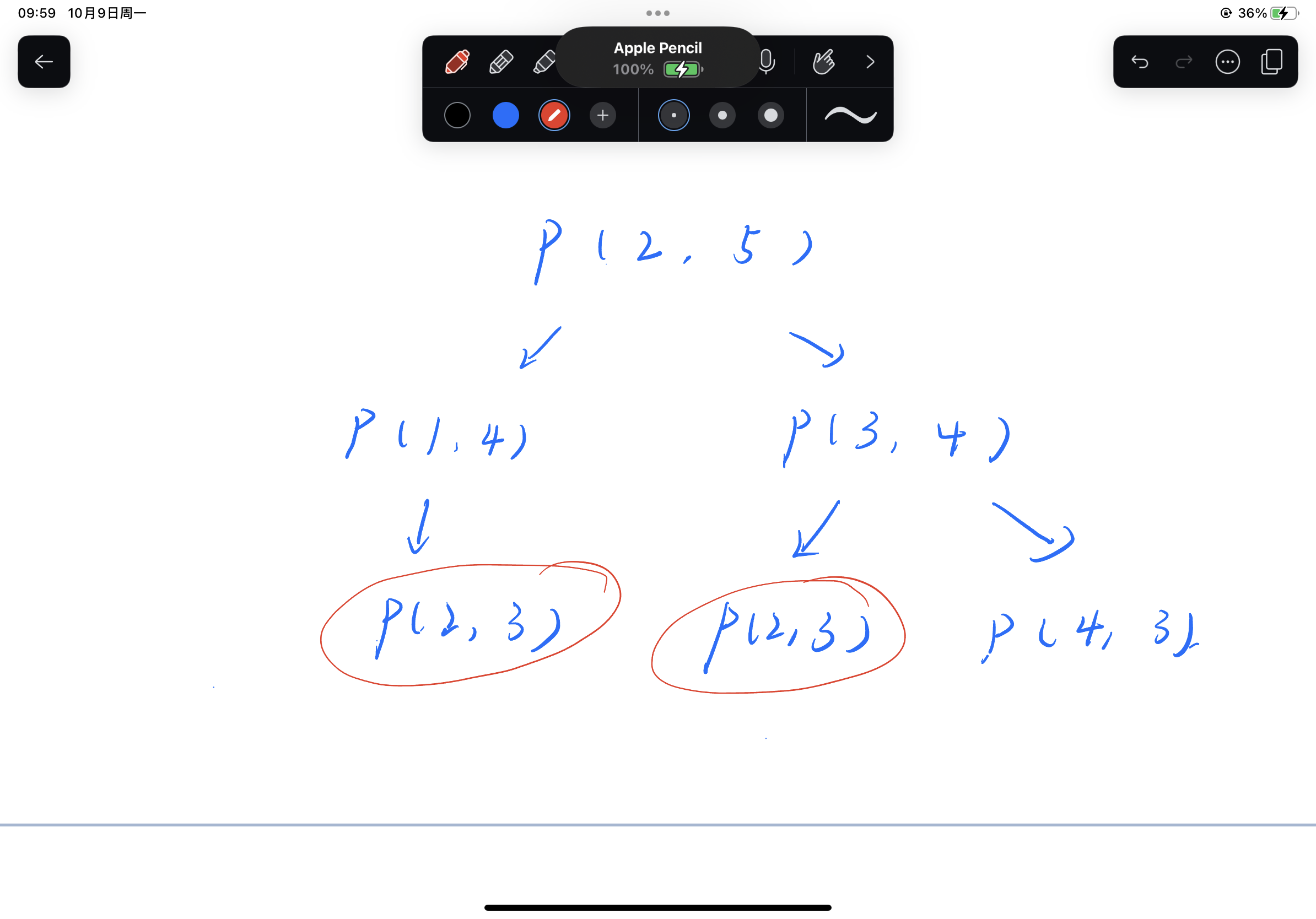
我们可以将该函数往下推演 我们会发现会出现两个相同的结果
如果继续往下展开的话则肯定会有重复的部分 所以说我们最好能将这些函数的结果记录下来 避免重复计算
我们选择使用一个二维数组存储每个函数的计算结果
vector<vector<int>> dp(n + 1 , vector<int>(rest + 1)); for (int i = 0 ; i < n + 1 ; i++ ) { for (int j = 0; j < rest + 1 ; j++) { dp[i][j] = -1; } }
这个二维数组 i j 分别标识当前位置和剩余步数
该数组的值表示在当前位置下走剩余步数能走到目的地有多少种解法
我们首先全部初始化为-1
int _process2(int cur , int rest , int aim , int n , vector<vector<int>>& dp)
{if (dp[cur][rest] != -1){return dp[cur][rest];}int ans = 0;if (rest == 0){ans = cur == aim ? 1 : 0;}else if (cur == 1){ans = _process2(2 , rest-1 , aim , n , dp);}else if (cur == n){ans = _process2(n-1 , rest-1 , aim , n , dp);} else {ans = _process2(cur -1 , rest -1 , aim , n , dp ) + _process2(cur +1 , rest -1 , aim , n , dp); } dp[cur][rest] = ans;return ans;}
之后在我们的函数中 如果数组中有结果 我们就直接返回 如果没有结果我们就将结果记录在数组中后返回 也能得到一样的结果
动态规划
我们以cur为横坐标 rest为纵坐标画一个图 并且将cur为0的时候值填入图中
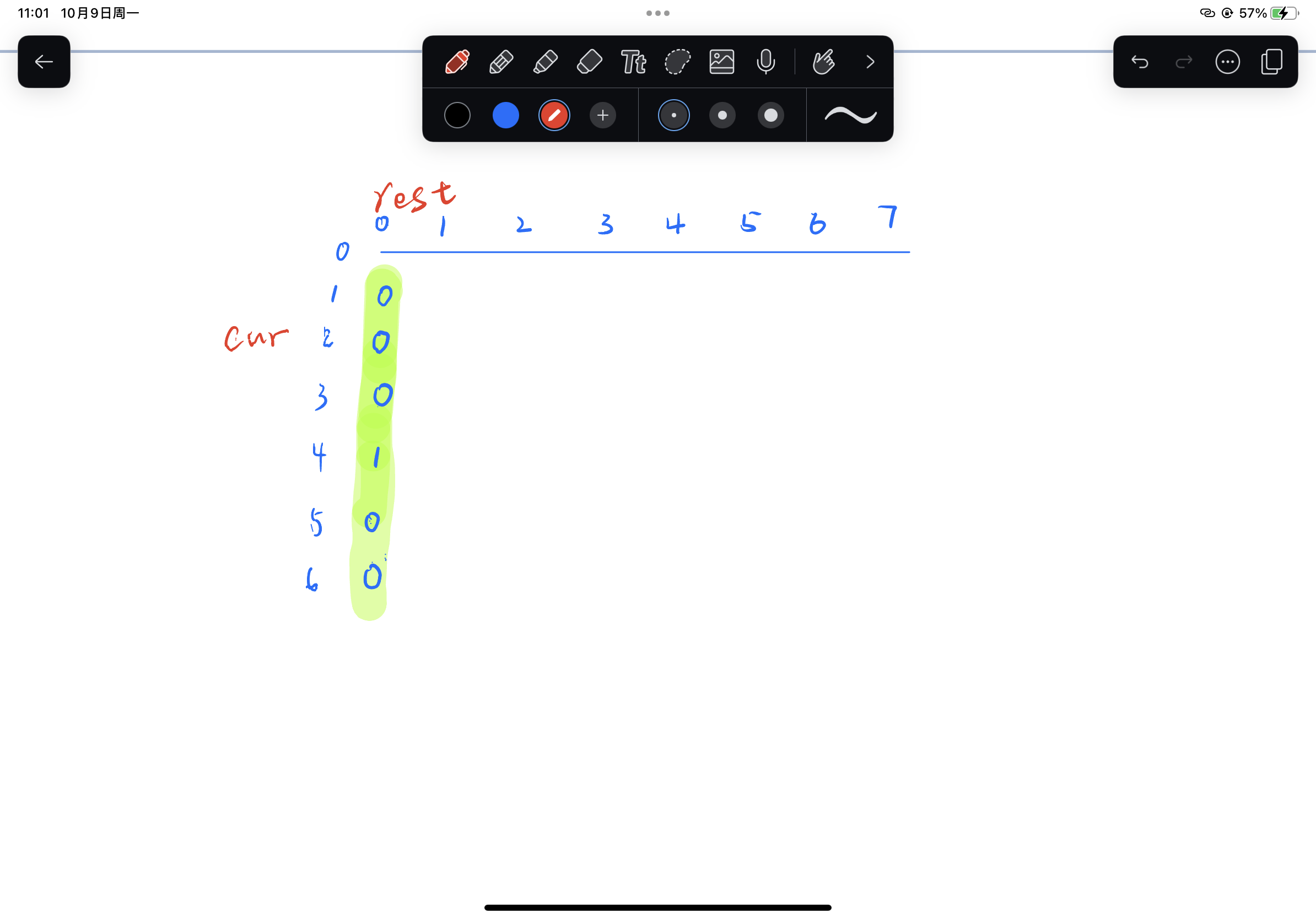
当cur为1的时候 我们回顾下我们的代码 我们会发现 此时该格上的数字只依赖于 dp[2][rest-1]
当cur为n的时候 我们回顾下之前的带啊吗 我们会发现 此时该格上的数字只依赖于 dp[n-1][rest-1]
当cur介于两者之间的时候 此时该格上的数字依赖于两种路径
dp[cur-1][rest-1] + dp[cur+1][rest-1]
如下图
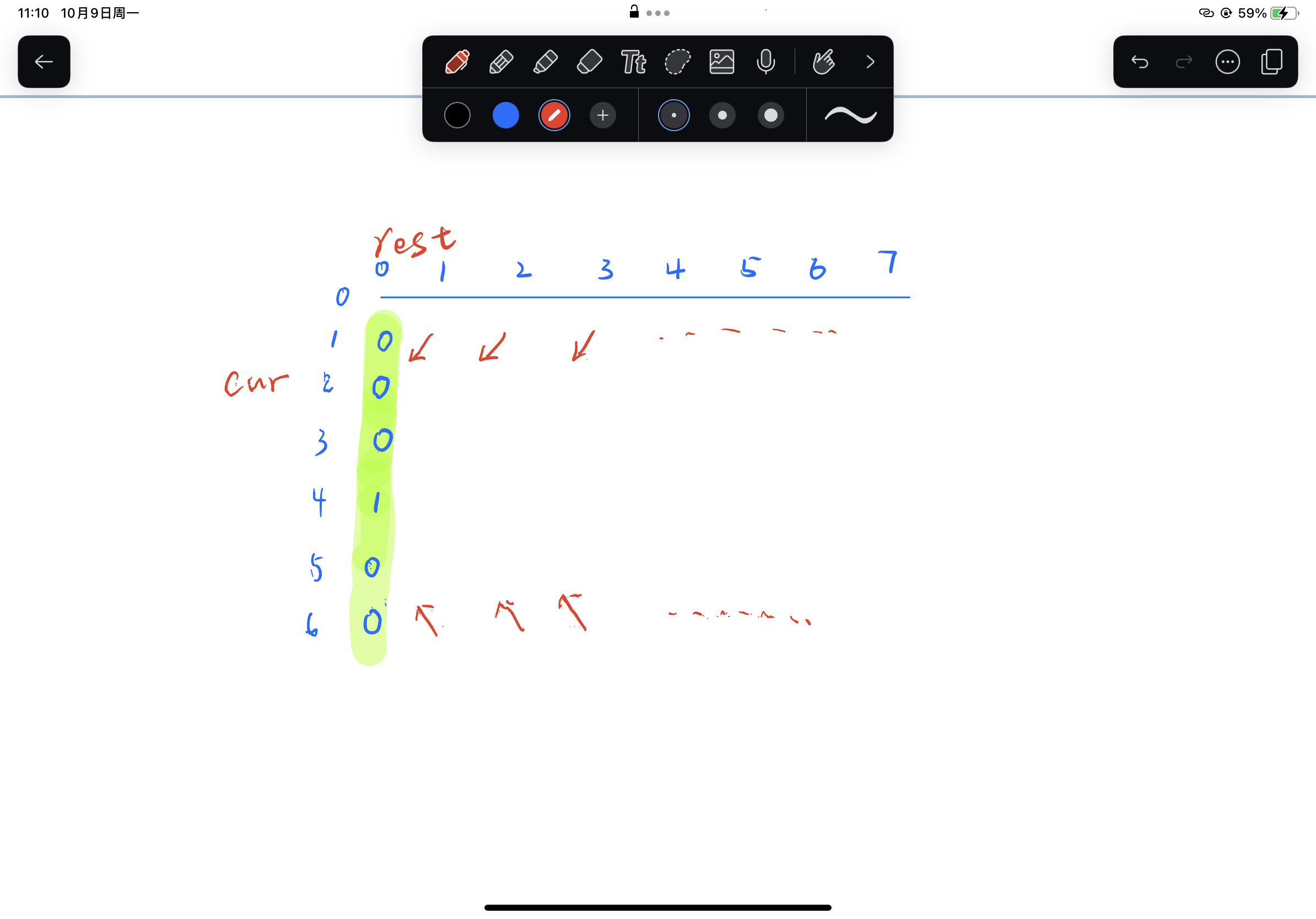
那么我们既然有了第一列的数字 我们就可以推出整个dp数组的数值
从而我们就能得出 当前为start 还有k步要走的时候 我们有几种路径
代码表示如下
int process3(int cur , int rest , int aim , int n)
{vector<vector<int>> dp(n + 1 , vector<int>(rest + 1)); for (int i = 0 ; i < n + 1 ; i++ ) { for (int j = 0; j < rest + 1 ; j++) { dp[i][j] = 0; } } // row 1 dp[aim][0] = 1; for (int r = 1 ; r <= rest ; r++) { dp[1][r] = dp[2][r-1]; for (int c = 2 ; c < n ; c++) { dp[c][r] = dp[c-1][r-1] + dp[c+1][r-1]; } dp[n][r] = dp[n-1][r-1]; } return dp[cur][rest];
}
这就是完整的解决动态规划问题的步骤
先后选牌问题
初级递归
假设现在给你一个数组 长度为N (N > 0) 数组内部储存着int类型的值 大小为(1~100)
现在两个人先后选数字 有如下规定
- 只能选择最边界的数字
- 如果这个数字被选择了 则从数组中移除
那么我们其实可以写出先选和后选两个函数
一开始我们写出的递归函数如下
int f(vector<int>& arr , int L , int R)
int g(vector<int>& arr , int L , int R)
这里两个函数的意义分别是
- f优先选择的最大值
- g后手选择的最大值
参数的含义是
- arr 数组
- L 左边界
- R 右边界
代码表示如下
int f(vector<int>& arr , int L , int R)
{ if (L == R) { return arr[L]; } int p1 = arr[L] + g(arr , L + 1 , R ); int p2 = arr[R] + g(arr , L , R - 1); return max(p1 , p2);
} int g(vector<int>& arr , int L , int R)
{ if (L == R) { return 0; } int p1 = f(arr , L + 1 , R);int p2 = f(arr , L , R -1);return min(p1 , p2);
}
这里解释下为什么g函数中要取最小值
因为先手的人可能会拿走L或者R 给我们造成p1 或者 p2两种结果
因为先手的人要赢 所以说只可能会给我们最差的一种结果 所以一定会是较小的那个值
初级动态规划
这里变化的参数实际上就只有左边界和右边界
我们就可以围绕着这两个边界来建表
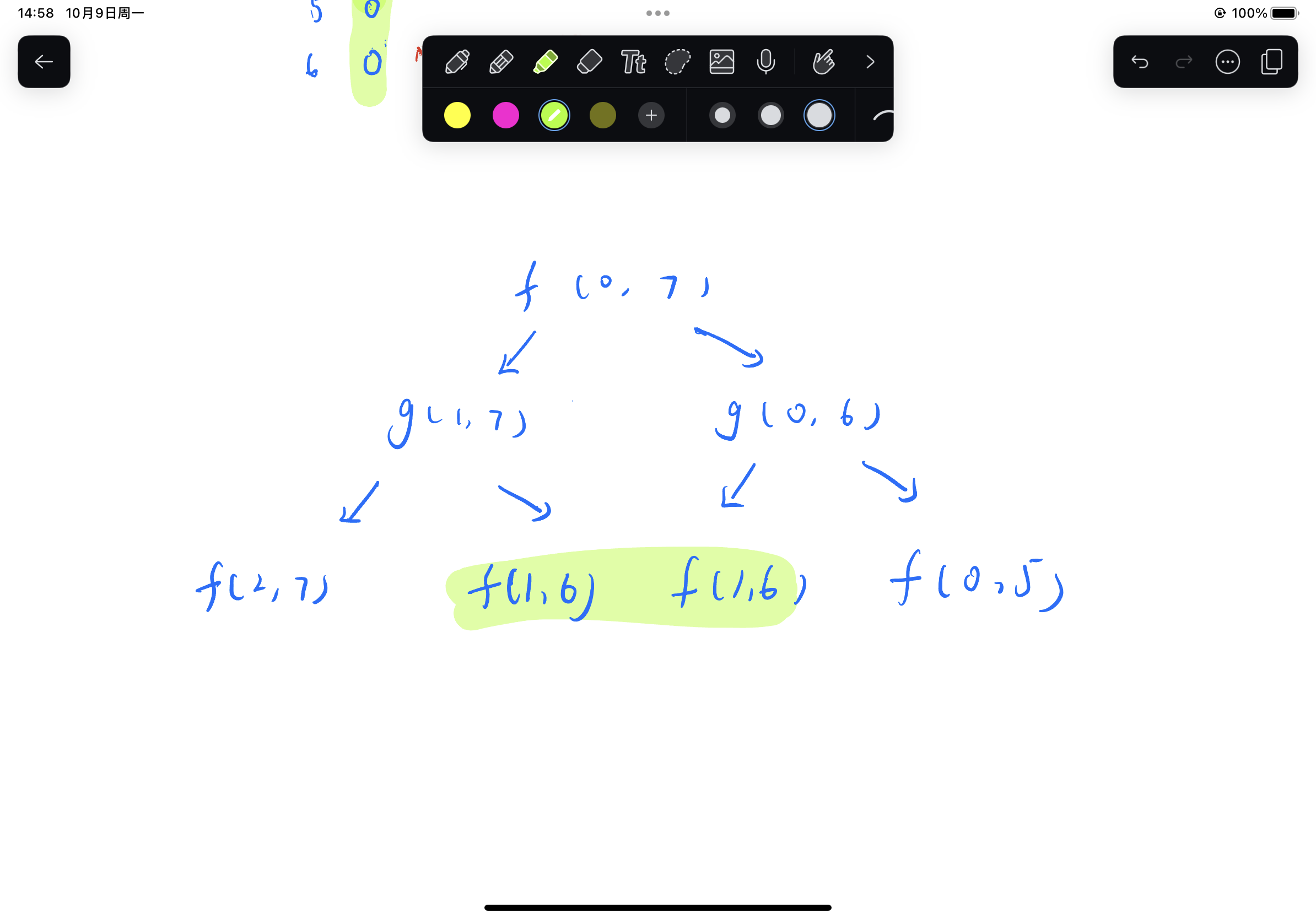
如果按照函数的依赖关系展开 我们很快就会发现重复项
所以说我们要围绕着重复项建表来达到动态规划的效果
而由于这里有两个函数 f 和 g 所以说 我们要建立两张表
我们以为L为横坐标 R为纵坐标建立两张表
L和R的范围是1 ~ R+1
代码表示如下
int _f2(vector<int>& arr , int L , int R , vector<vector<int>>& fmap , vector<vector<int>>& gmap)
{ if (fmap[L][R] != 0) { return fmap[L][R]; } int ans = 0; if ( L == R) { ans = arr[L]; } else { int p1 = arr[L] + _g2(arr , L+1 , R , fmap , gmap); int p2 = arr[R] + _g2(arr , L , R-1 , fmap , gmap); ans = max(p1 , p2); } fmap[L][R] = ans; return ans; }
int _g2(vector<int>& arr , int L , int R , vector<vector<int>>& fmap , vector<vector<int>>& gmap)
{ if (gmap[L][R] != 0){return gmap[L][R];}int ans = 0;if (L == R){ ans = 0;} else { int p1 = _f2(arr , L , R -1 , fmap , gmap);int p2 = _f2(arr , L + 1 , R , fmap , gmap);ans = min(p1 , p2);} gmap[L][R] = ans;return ans;
}动态规划
我们以L为横坐标 R为纵坐标画一个gmap图 并且将L == R的时候的值填入图中
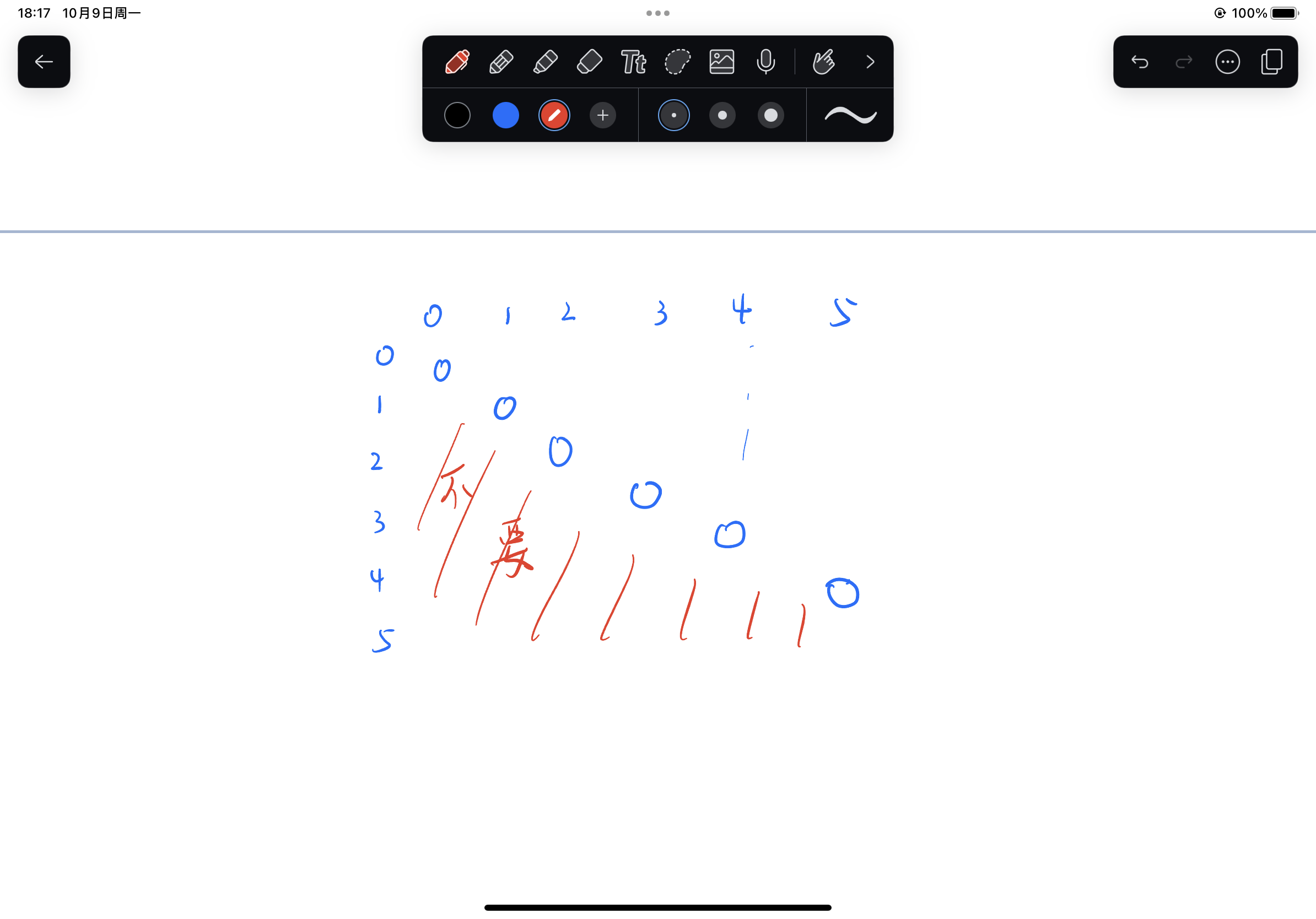
我们可以发现该图的左下角我们是不需要的因为L不可能大于R
那么我们的gmap上右上角的随机一点是依赖于什么呢?
回归到我们最初的递归方程中
_f2(arr , L , R -1 , fmap , gmap);
_f2(arr , L + 1 , R , fmap , gmap);
我们可以发现是依赖于fmap的 L R-1 以及 L+1 R
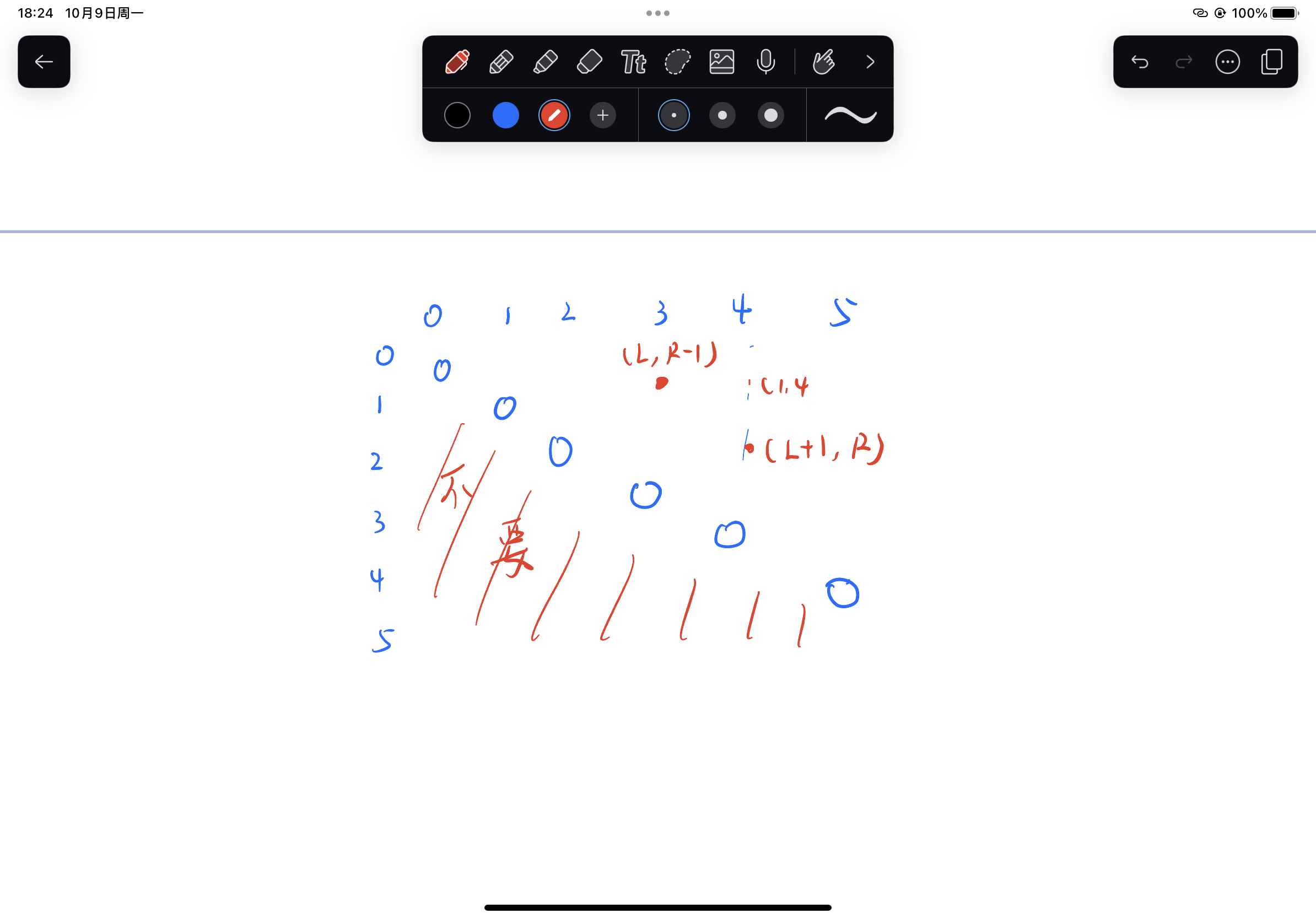
如果映射到fmap中 我们可以发现刚好是斜对角线上的两点 既然我们现在知道了斜对角线上的值 我们现在就可以开始填写这两张map表了
代码表示如下
int f3(vector<int>& arr , int L , int R)
{vector<vector<int>> fmap( R + 1, vector<int>(R+1));for (int i = 0 ; i < R + 1 ; i++){for (int j = 0; j < R + 1 ; j++){fmap[i][j] = 0;if (i == j){fmap[i][j] = arr[i];}}}vector<vector<int>> gmap( R+1 , vector<int>(R+1));for (int i = 0 ; i < R + 1 ; i++){for (int j = 0; j < R + 1 ; j++){gmap[i][j] = 0;}} for (int startcol = 1 ; startcol < R + 1; startcol++ ){int col = startcol;int row = 0;while (col < R + 1){fmap[row][col] = max(gmap[row][col-1] + arr[row] , gmap[row+1][col] + arr[col]);gmap[row][col] = min(fmap[row][col-1] , fmap[row+1][col]);row++;col++;}}return fmap[L][R];
}其实最关键的代码就是这两行
fmap[row][col] = max(gmap[row][col-1] + arr[col] , gmap[row+1][col] + arr[row]);gmap[row][col] = min(fmap[row][col-1] , fmap[row+1][col]);
我们可以发现 这其实就是将原来代码中的函数
int p1 = arr[L] + _g2(arr , L+1 , R , fmap , gmap); int p2 = arr[R] + _g2(arr , L , R-1 , fmap , gmap); ans = max(p1 , p2);
变成了表中的数字相加
这就是动态规划的一般套路