向量的【范数】：模长的推广，柯西不等式_哔哩哔哩_bilibili

 

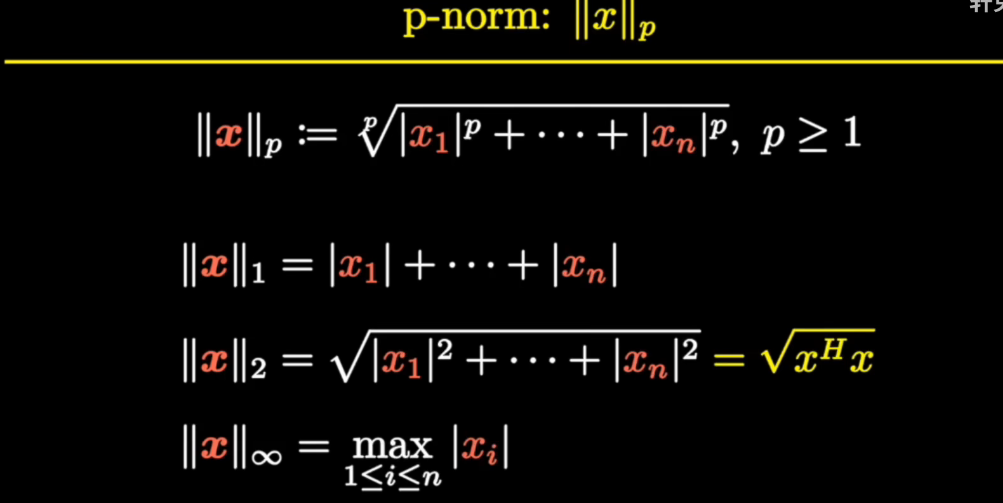
范数理解（0范数，1范数，2范数）_一阶范数-CSDN博客

 

正定矩阵（Positive Definite Matrix）是指一个对称矩阵A，对于任意非零向量x，都满足x^T * A * x > 0，其中^T表示向量的转置。换句话说，正定矩阵的所有特征值都大于零。

半正定矩阵（Positive Semidefinite Matrix）是指一个对称矩阵A，对于任意非零向量x，都满足x^T * A * x ≥ 0。换句话说，半正定矩阵的所有特征值都大于等于零。

这里的正不正定及是否半正定可由特征值判断，之前都学了啥？？？？

矩阵的【范数】：也是一种长度

矩阵刻画的是一种线性变换，如何衡量变换的长度，有一种想法是在某种范数的情况下考虑某种单位向量，然后在变换后取变换最长的长度作为向量的长度：

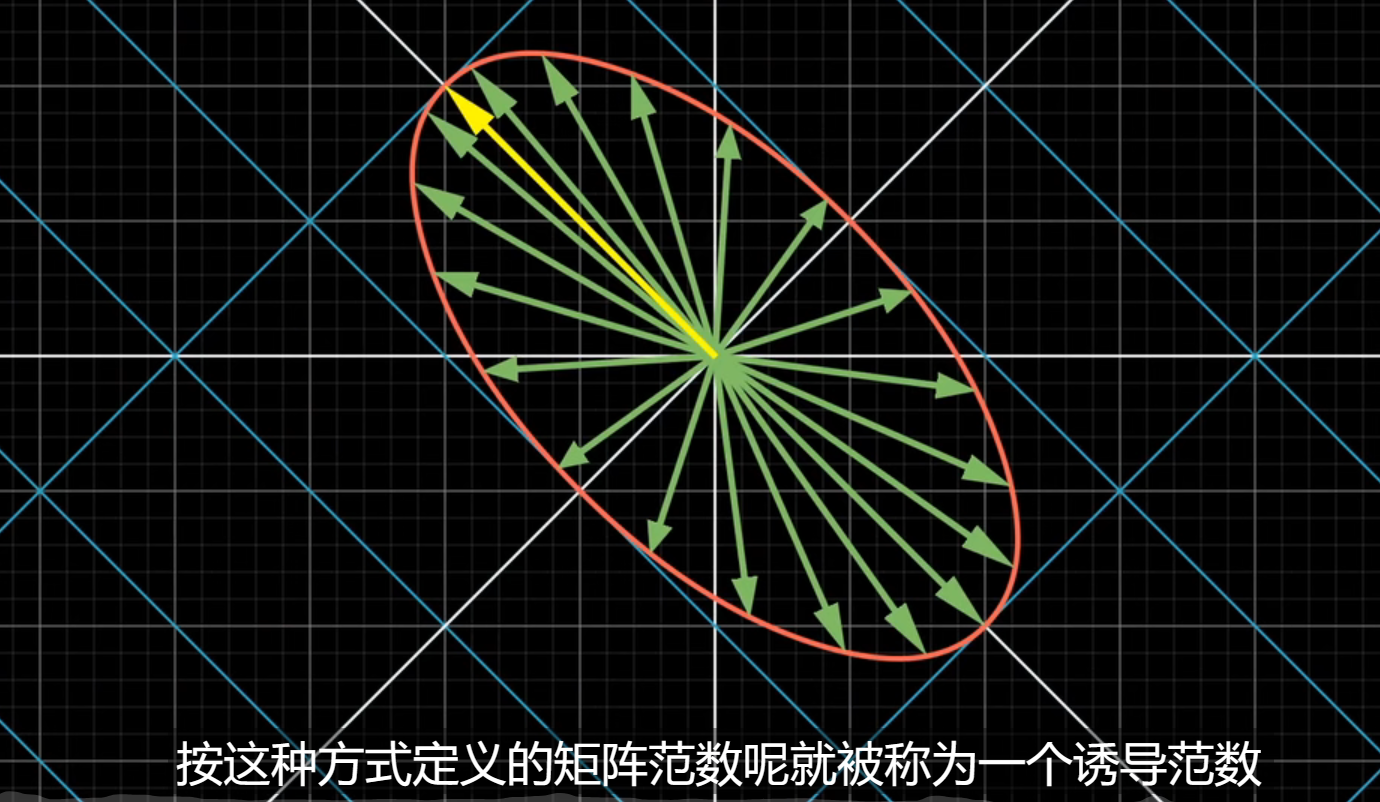
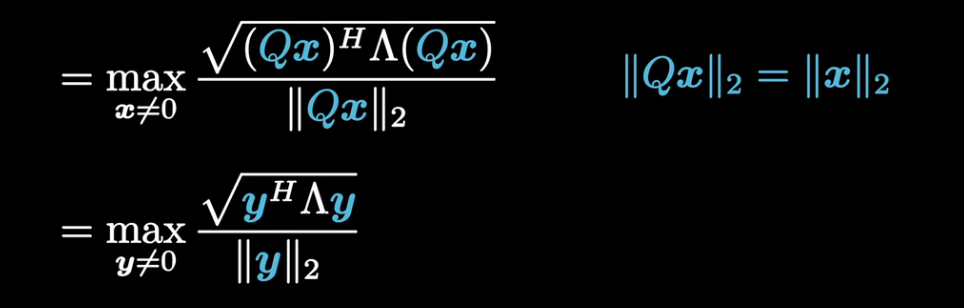
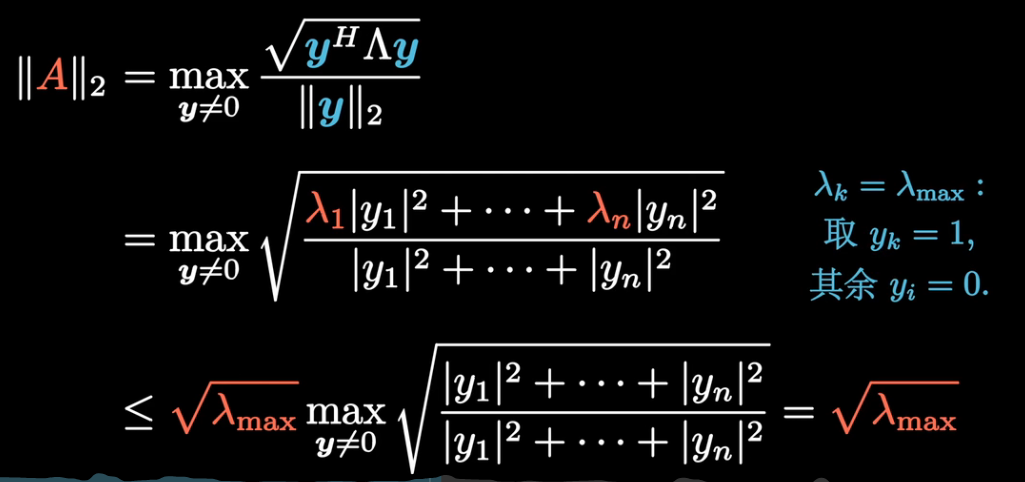
 矩阵的一范数，等于其最大的列和

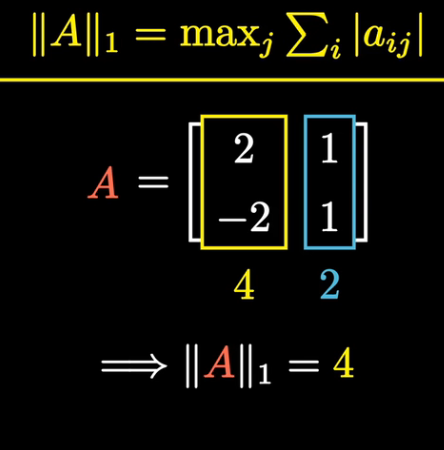
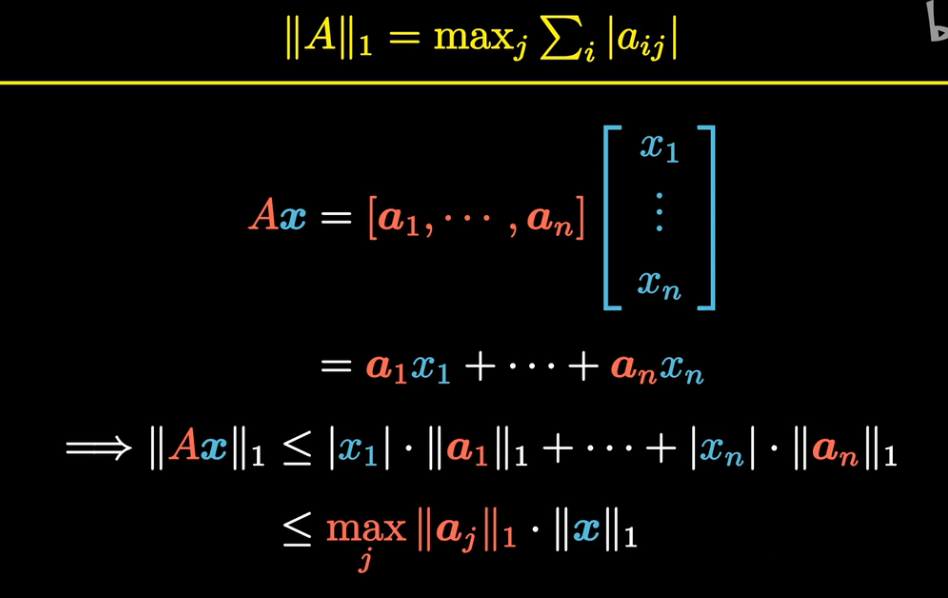
矩阵的无穷范数 是矩阵的最大行和

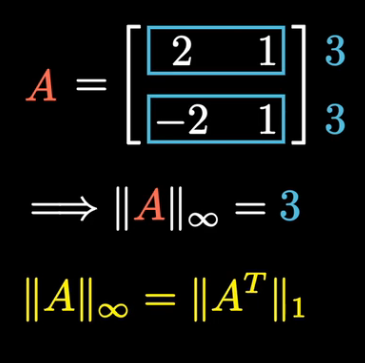
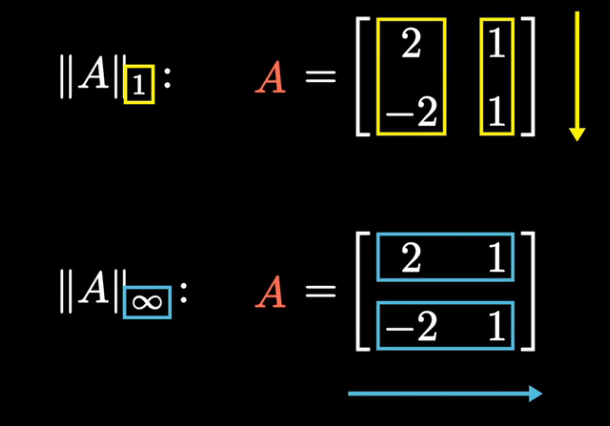
Frobenius norm 

我这脑袋瓜子记不住啊，用到的时候再看看。。。