传送门:AtCoder Regular Contest 166 - AtCoder
一直修炼cf,觉得遇到了瓶颈了,所以想在atcode上寻求一些突破,今天本来想尝试vp AtCoder Regular Contest 166,但结局本不是很好,被卡了半天,止步于B题。不过确实,感觉AtCoder的题目还是很不错的,一改cf的很多惯性思路。
这里借用了大佬樱雪喵的题解链接,大佬的传送门如下Atcoder Regular Contest 166 - 樱雪喵 - 博客园 (cnblogs.com)
B - Make Multiples
问题陈述
给你一个整数序列 A=(A1,…,AN),以及正整数 a,b 和 c。
你可以对这个数列进行以下运算,次数不限,可能为零。
- 选择一个整数 i,使得 1≤i≤N.将 Ai 替换为 Ai+1。
你的目标是使数列 A 至少包含一个 a 的倍数,至少一个 b 的倍数,以及至少一个 c 的倍数。求实现这一目标所需的最少运算次数。
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
const ll MX=0x3f3f3f3f3f3f3f3f;int n,m;
int lcm(int a,int b){return a*b/__gcd(a,b);
}
void icealsoheat(){int a,b,c;cin>>n>>a>>b>>c;vector dp(n+5,vector(10,MX));int op[]={1,a,b,lcm(a,b),c,lcm(a,c),lcm(c,b),lcm(lcm(a,c),b)};dp[0][0]=0;for(int i=0;i<n;i++){int x;cin>>x;for(int j=0;j<8;j++){for(int k=0;k<8;k++){if((j&k)==0){// dp[i+1][j|k]=min(dp[i+1][j|k],dp[i][j]+op[k])if(x%op[k]==0){dp[i+1][j|k]=min(dp[i+1][j|k],dp[i][j]);}else{dp[i+1][j|k]=min(dp[i+1][j|k],dp[i][j]+(x/op[k]+1ll)*op[k]-x);}}}}// cout<<dp[n][7]<<"\n";}cout<<dp[n][7]<<"\n";}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;// cin>>_;while(_--){icealsoheat();}
}C - LU / RD Marking
问题陈述
有一个网格,网格中有 H 行和 W 列。
这个网格有H(W+1)条垂直边和W(H+1)条水平边,共计H(W+1)+W(H+1)条(另见输入/输出示例中的数字)。请考虑通过以下两种操作来标记这些边。
- 操作 (1)**:选择一个正方形,在进行此操作时,其左边缘和上边缘均未标记。标记该正方形的左边缘和上边缘。
- 操作 (2):选择一个右边和下边在执行此操作时没有标记的正方形。标出该正方形的右边和下边。
求操作(1)和操作(2)执行任意多次(可能为零)时,最终被标记的边的可能集合的数量,模为 998244353998244353。
您有 T 个测试案例需要解决。
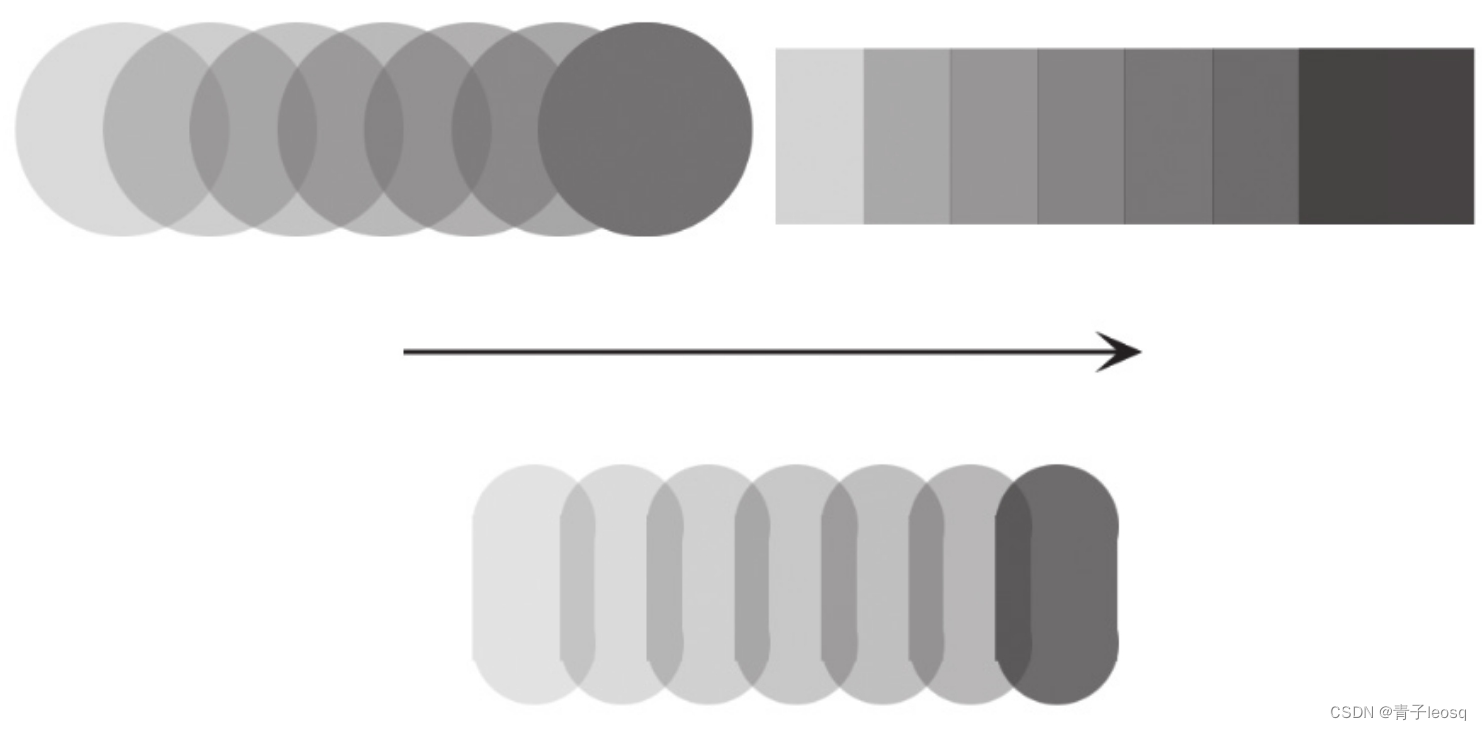
这里要借用官方题解的图例:
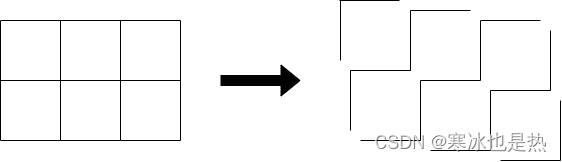
由此将方块拆开找规律。
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
const ll MX=0x3f3f3f3f3f3f3f3f;
int n,m;
int dp[2000008];
int sum[2000008];
int kuai(int a,int b){int ans=1;while(b){if(b&1)ans=ans*a%N;b>>=1;a=a*a%N;}return ans%N;
}
void icealsoheat(){cin>>n>>m;if(n>m)swap(n,m);int ans=sum[n]*kuai(dp[2*n],m-n)%N;cout<<ans<<"\n";
}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;cin>>_;dp[0]=1;dp[1]=2;for(int i=2;i<=2000005;i++){dp[i]=dp[i-1]+dp[i-2];dp[i]%=N;}sum[0]=1;for(int i=1;i<=1000000;i++){sum[i]=sum[i-1]*dp[2*i-1]%N*dp[2*i-1]%N;}while(_--){icealsoheat();}
}D - Interval Counts
因为这题还是比较好想的所以直接上代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
const ll MX=0x3f3f3f3f3f3f3f3f;
int n,m;
void icealsoheat(){cin>>n;vector<int>x;vector<int>y;x.push_back(-2e9);y.push_back(0);for(int i=1;i<=n;i++){int xx;cin>>xx;x.push_back(xx);}vector<PII>ve;for(int i=1;i<=n;i++){int xx;cin>>xx;y.push_back(xx);}ll maxx=2e9;int id=0;for(int i=1;i<=n;i++){if(y[i]==y[i-1])continue;else if(y[i]>y[i-1])ve.push_back({x[i-1]+1,y[i]-y[i-1]});else{int now=y[i-1]-y[i];while(id<ve.size()&&ve[id].second<=now){maxx=min(x[i]-1-ve[id].first,maxx);now-=ve[id].second;id++;}if(now&&id<ve.size()){ve[id].second-=now;maxx=min(x[i]-1-ve[id].first,maxx);}}}if(maxx>1e9)printf("-1\n");else printf("%lld\n",maxx);}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;// cin>>_;while(_--){icealsoheat();}
}