目录
1、平稳性的Daniel检验
(1)Spearman相关系数假设检验
(2)时间序列平稳性的Danniel假设检验
案例
【模型分析】
1、原始数据at的平稳性检验
2、一阶差分序列的平稳性检验
3、二阶差分序列的平稳性检验
4、建立AR(2)模型
【模型求解】
1、平稳性的Daniel检验
(1)Spearman相关系数假设检验
设二维总体(X,Y)的样本观测值为:(x1,y1),(x2,y2),…,(xn,yn), 得各分量X,Y的样本为(x1,…,xn),(y1,…,yn),设(x1,…,xn)的秩统计量为R1,R2,…,Rn;(y1,y2,…,yn)的秩统计量为S1,S2,…,Sn。当X,Y紧密相关时,这两组秩统计量也是紧密相关的
向量的秩:
向量的秩是指矩阵中非零行向量组成的最大线性无关组的向量个数。在线性代数中,我们常常将向量表示为列向量,也即 n×1的矩阵。
一个矩阵的秩是指它的列向量或行向量中线性无关的向量的个数。可以用初等变换将矩阵变换为行最简形,行最简形的矩阵就是阶梯型矩阵。阶梯型矩阵的非零行的个数即为矩阵的秩。
对于 n × m 的矩阵 A,它的秩记作 rank(A)。秩的性质包括:
1. rank(A) ≤ min(n, m),即矩阵的秩不会超过它的行数和列数中的较小值。
2. 对于同型矩阵 A 和 B,如果 A 可以通过基本行(列)运算转换为 B,那么它们的秩相等。
3. 对于同型矩阵 A 和 B,有 rank(A + B) ≤ rank(A) + rank(B)。秩的求解方法包括高斯消元法、矩阵的特征值特征向量等。
(x1,…,xn)的秩统计量为R1,R2,…,Rn:
在统计学中,对于给定的一组数据 (x1, x2, ..., xn),可以计算出一系列的秩统计量 R1, R2, ..., Rn,用于描述数据的排序性质。每个秩统计量 Ri 表示对应数据 xi 在原始数据中的排名。
秩统计量常用于非参数统计方法,特别是在样本数据不服从正态分布或具有明显偏斜的情况下。它们提供了一种基于排序的方法来分析数据,不受异常值的影响,并可以在不依赖具体分布的情况下得到一些推断性的结论。
以下是对每个秩统计量的解释:
- R1 表示 x1 在排序后的数据中的排名。
- R2 表示 x2 在排序后的数据中的排名。
- ...
- Rn 表示 xn 在排序后的数据中的排名。对于具体的数据样本,可以通过对原始数据进行排序,然后分配相应的秩统计量来计算每个数据的排名。排名方式可以根据需要选择是按升序还是降序进行排列。
通过计算秩统计量,可以进行一系列非参数的统计检验、回归分析和描述性统计分析,例如秩和检验、秩相关分析和秩和相关系数等。这些方法可以提供一种有效的手段来处理各种类型的数据,特别是对于小样本或不满足正态分布假设的情况下。
定义Spearman相关系数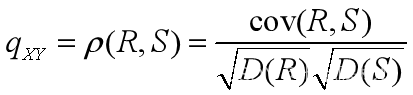
经过运算,可以证明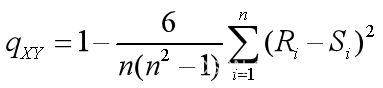
对Spearman相关系数,可以作假设检验: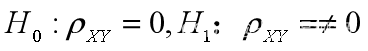
在H0成立时,统计量
对给你的显著水平α,查自由度为n-2的t分布的临界值tα/2(n-2),当|T|≤tα/2(n-2)时,接受H0,否则决绝H0.
(2)时间序列平稳性的Danniel假设检验
设时间序列样本a1,a2,…,an为Xt的样本,记at的秩为Rt=R(at),考虑变量(t,Rt),t=1,2,…,n的Spearman相关系数为
构造统计量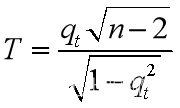
作假设检验:H0:序列Xt平稳;H1:序列Xt非平稳(上升或下降)
(H0的意思t和Rt不相关,即相关系数为0,H1的意思t和Rt相关,即Rt随t增大呈线性递增或递减)
Danniel检验方法:对给定的显著系数α,查自由度为n-2的t分布的临界值tα/2(n-2),若统计量T满足|T|>tα/2(n-2),则拒绝H 0,即认为序列非平稳,若|T|≤tα/2(n-2),接受H0,即Xt是平稳的。
案例
| 月份t | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售收入yt | 533.8 | 574.6 | 606.9 | 649.8 | 705.1 | 772.0 |
| 月份t | 7 | 8 | 9 | 10 | 11 | |
| 销售收入yt | 816.4 | 892.7 | 963.9 | 1015.1 | 1102.7 |
用AR模型预测12月份的销售额。
【模型分析】
1、原始数据at的平稳性检验
设1-11月份销售数据为at,根据公式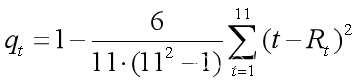 计算得到Spearman相关系数为qt=1.根据公式
计算得到Spearman相关系数为qt=1.根据公式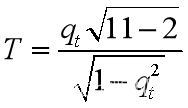
α=0.05,计算得到T统计量为+∞,即|T|> tα/2(11-2)=2.2622,即拒绝H0,认为Xt非平稳。即at非平稳时间序列。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
Rt=tiedrank(at);
n=length(Rt);
t=1:n;
dt=t-Rt;
qt=1-6/n/(n^2-1)*sum(dt.^2);
T=qt*(n-2)^0.5/(1-qt^2)^0.5;
2、一阶差分序列的平稳性检验
令bt=at-at-1,t=2,3,…,11,将bt代入【4】和【5】,计算得到T统计量为T= 3.6934>tα/2(10-2)=2.3,即bt也非平稳序列。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
bt=diff(at);
Rt=tiedrank(bt);
n=length(Rt);
t=1:n;
dt=t-Rt;
qt=1-6/n/(n^2-1)*sum(dt.^2);
T=qt*(n-2)^0.5/(1-qt^2)^0.5;
3、二阶差分序列的平稳性检验
取ct=bt-bt-1,t=2,3,…,10,将ct代入【4】和【5】,计算,得到统计量T= 0.4934<tα/2(9-2)=2.36,即ct是平稳序列。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
bt=diff(at);
ct=diff(bt);
Rt=tiedrank(ct);
n=length(Rt);
t=1:n;
dt=t-Rt;
qt=1-6/n/(n^2-1)*sum(dt.^2);
T=qt*(n-2)^0.5/(1-qt^2)^0.5;
4、建立AR(2)模型
根据上面的检验,可建立自回归模型AR(2)对at进行预测: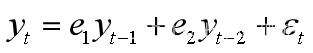 e1,e2是待定参数,εt是随机扰动。
e1,e2是待定参数,εt是随机扰动。
【模型求解】
根据表中数据,采用最小二乘拟合,求得模型为
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
m=ar(at',2);
>> mm =
Discrete-time AR model: A(z)y(t) = e(t)A(z) = 1 - 1.95 z^-1 + 0.9431 z^-2
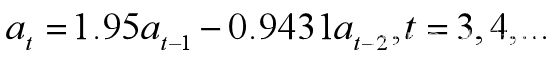
将a10,a11代入上公式,预测12月份销售额为a12=1192.9。并将预测值和实测值对比显示在下图。
at=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
for k=3:12at1(k)=1.95*at(k-1)-0.9431*at(k-2);
end
t=1:9;
at=at(3:end);
at1=at1(3:end-1);
plot(t,at,‘*’,t,at1,‘+’),legend(‘实测值’,‘预测值')
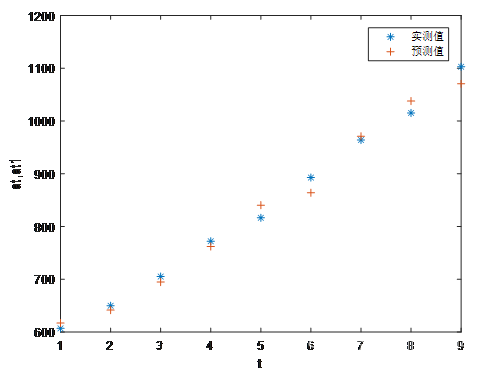
另外:matlab时间序列工具箱有AR(2)拟合函数m=ar(at',2);