贝叶斯学习

贝叶斯学习主要是依靠先验概率来推出后验概率，然后更具后验概率去验证。其主流分为朴素贝叶斯和高斯分布下的贝叶斯估计。

相关概率知识

**先验概率：**指根据以往经验和分析。在实验或采样前就可以得到的概率。

**后验概率：**指某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。

**联合概率：**指是事件同时发生的概率，例如现在A,B两个事件同时发生的概率，记为P(A,B)、P(A∩B)、P(AB)。
若A、B事件相互独立，则存在
$$P(AB)=P(A)P(B)$$
条件概率：指一个事件发生后另一个事件发生的概率，一般情况下B表示某一个因素，A表示结果，P(A|B)表示在因素B的条件下A发生的概率，即由因求果，其计算公式如下：
$$P(B|A)=\frac{P(AB)}{P(A)}$$
若A、B事件相互独立，则存在
$$P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A)P(B)}{P(A)}=P(B)$$
全概率公式：
$$P(A)=\sum _{i=1}^{n}P(B_i)P(A|B_i)$$
贝叶斯公式：
$$P(B_i|A)=\frac{P(B_{i}A)}{P(A)}=\frac{P(A|B_i)P(B)}{P(A)}=\frac{P(A|B_i)P(B)}{{\sum }_{i=1}^{n}P(B_i)P(A|B_i)}$$

高斯分布：

若随机变量$X$满足$X\sim N(\mu ,{\sigma }^2)$，其中$\mu$与$\sigma$分别为均值与标准差
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
标准差：
$$S=\sqrt{\frac{\sum (x_i-\overline{x}{)}^2}{m-1}}$$
协方差：
$$E=\frac{\sum (x_i-\overline{x})(y_i-\overline{y})}{m-1}$$
协方差矩阵：
$$\left[\begin{array}{cccc}{E}_{11}& E_{12}& \cdots & E_{1n}\\ E_{21}& E_{22}& \cdots & E_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ E_{m1}& E_{m2}& \cdots & E_{mn}\end{array}\right]$$

朴素贝叶斯

对于$x_i$离散样本的情况下，其中$D_c$为对样本$c$的数目统计：
$$P(c)=\frac{||D_c||}{||D||}$$

$$P(x_i|c)=\frac{|D_{x_i,c}|}{|D_c|}$$

对于$x_i$为连续样本的情况下：
$$P(x_i|c)=\frac{1}{\sqrt{2\pi }{\sigma }_{c,j}}{e}^{-\frac{(x_i-{\mu }_{c;i}{)}^2}{2{\sigma }_{c,i}^2}}$$
在对于多特征的样本，朴素贝叶斯假设各个特征独立，即特征A与B满足
$$P(AB)=P(A)P(B)$$
其中$c$为结果，$x$为特征
$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}\propto P(c)P(x|c)=P(c){\Pi }_{i=1}^{d}P(x_i|c)$$
为了避免出现出现$P(c)=0$的情况，采用拉普拉斯平滑进行处理
$$P(c)=\frac{||D_c||+1}{||D||+N}N为类别数$$

$$P(x_i|c)=\frac{||D_{c,i}||+1}{||D_c||+N_i}{N}_i为x_i可能取的类别数$$

多维正态密度贝叶斯

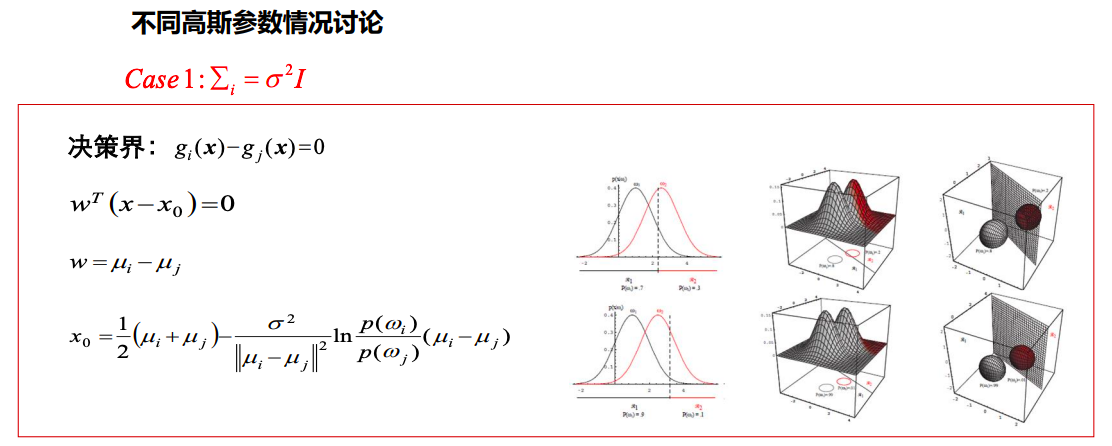
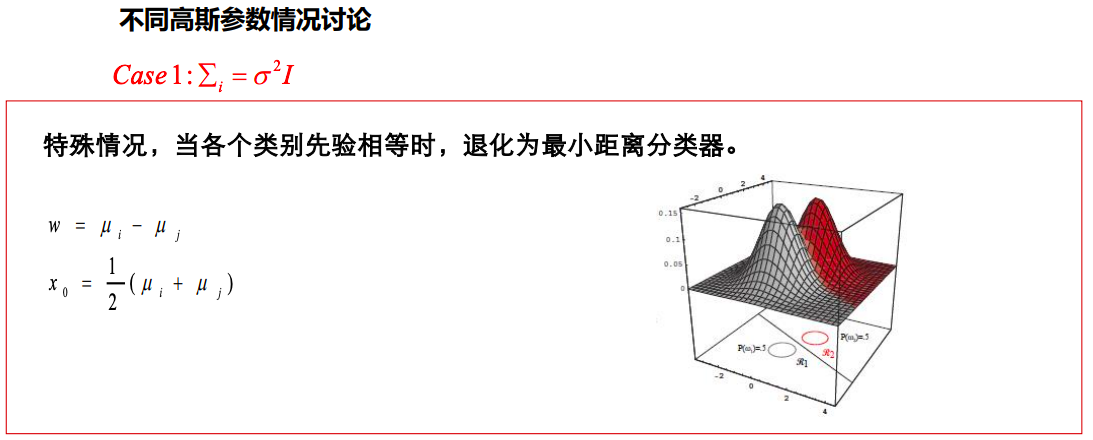
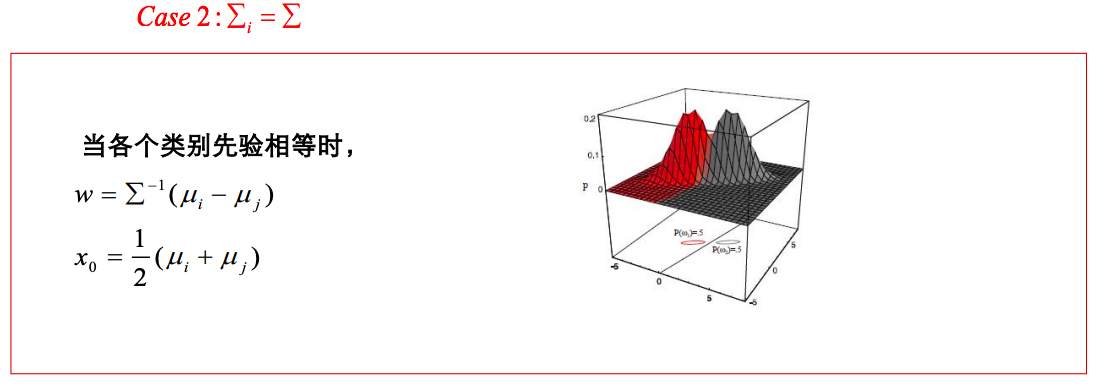
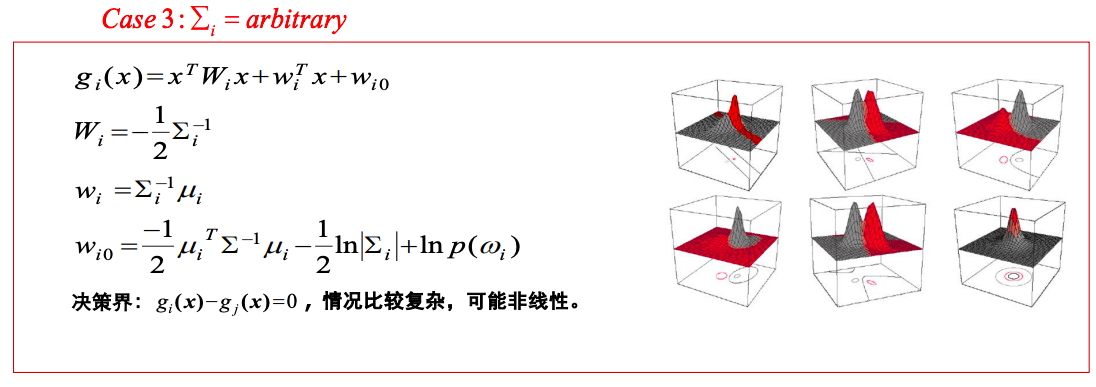
多维正态分布的概率密度$N\sim (\mu ,\Sigma )$，$\mu$，$\Sigma$分别为正态分布的均值与协方差矩阵
$$P(x)=\frac{1}{(2\pi {)}^{d/2}|\Sigma |}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$$