数据结构：选择题+编程题（每日一练）

选择题：

题一：

题二：

题三：

题四：

题五：

编程题：

题一：单值二叉树

思路一：

题二：二叉树的最大深度

思路一：

本人实力有限可能对一些地方解释和理解的不够清晰，可以自己尝试读代码，或者评论区指出错误，望海涵！

感谢大佬们的一键三连！感谢大佬们的一键三连！感谢大佬们的一键三连！

选择题：

题一：

1.一颗拥有1000个结点的树度为4，则它的最小深度是( )

A.5

B.6

C.7

D.8

答案解析：

如果这棵树每一层都是满的，则它的深度最小，假设它为一个四叉树，高度为h，则这个数的节点个数为(4^h - 1) / 3，当h = 5, 最大节点数为341，当h = 6, 最大节点数为1365，所以最小深度应该为6。

题二：

2.设一棵二叉树中有3个叶子结点，有8个度为1的结点，则该二叉树中总的结点数为( )个

A.11

B.12

C.13

D.14

答案解析：

        设Ni表示度为i的节点个数，则节点总数 N = N0 + N1 + N2

        节点个数于节点边的关系： N个节点的树有N-1个边

        边与度的关系：N - 1 = N1 + 2 * N2

        故：N0 + N1 + N2 - 1 = N1 + 2 * N2

        因此，得：N0 = N2 + 1

        回到原题，N0 = 3，N1 = 8，可得N2 = 2。

        因此答案是 3 + 8 + 2 = 13。

题三：

3.在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有( )个

A.4

B.5

C.6

D.7

答案解析：

        设度为i的节点个数为ni, 该树总共有n个节点,则n=n0+n1+n2+n3.

        有n个节点的树的总边数为n-1条.

        根据度的定义,总边数与度之间的关系为：n-1=0*n0+1*n1+2*n2+3*n3.

        联立两个方程求解,可以得到n0 = n2 + 2n3 + 1,  n0=6

题四：

4.下列关于二叉树的叙述错误的是( )

A.二叉树指的是深度为 2 的树

B.一个 n 个结点的二叉树将拥有 n-1 条边

C.一颗深度为 h 的满二叉树拥有 2^h-1 个结点（根结点深度为1）

D.二叉树有二叉链和三叉链两种表示方式

答案解析：

        A错误: 二叉树指最大孩子个数为2，即树的度为二的树。深度描述的为树的层数。

        B正确: 对于任意的树都满足：边的条数比节点个数少1，因为每个节点都有双亲，但是根节点没有

        C正确: 正确，参加二叉树性质

        D正确: 二叉链一般指孩子表示法，三叉连指孩子双亲表示法，这两种方式是二叉树最常见的表示方式，虽然还有孩子兄弟表示法，该中表示方式本质也是二叉链

题五：

5.下列关于堆的叙述错误的是（）

A.堆是一种完全二叉树

B.堆通常使用顺序表存储

C.小堆指的是左右孩子结点都比根结点小的堆

D.堆的删除是将尾部结点放到队顶后执行向下调整算法

答案解析：

堆是在完全二叉树的基础上进行了条件的限制，即：每个节点都比其孩子节点大，则为大堆；每个节点都比其孩子节点小则为小堆完全二叉树比较适合使用顺序结构存储。

堆删除：删的是堆顶元素，常见操作是将堆顶元素与堆中最后一个元素交换，然后对中元素个数减少一个，重新将堆顶元素往下调整故C错误

编程题：

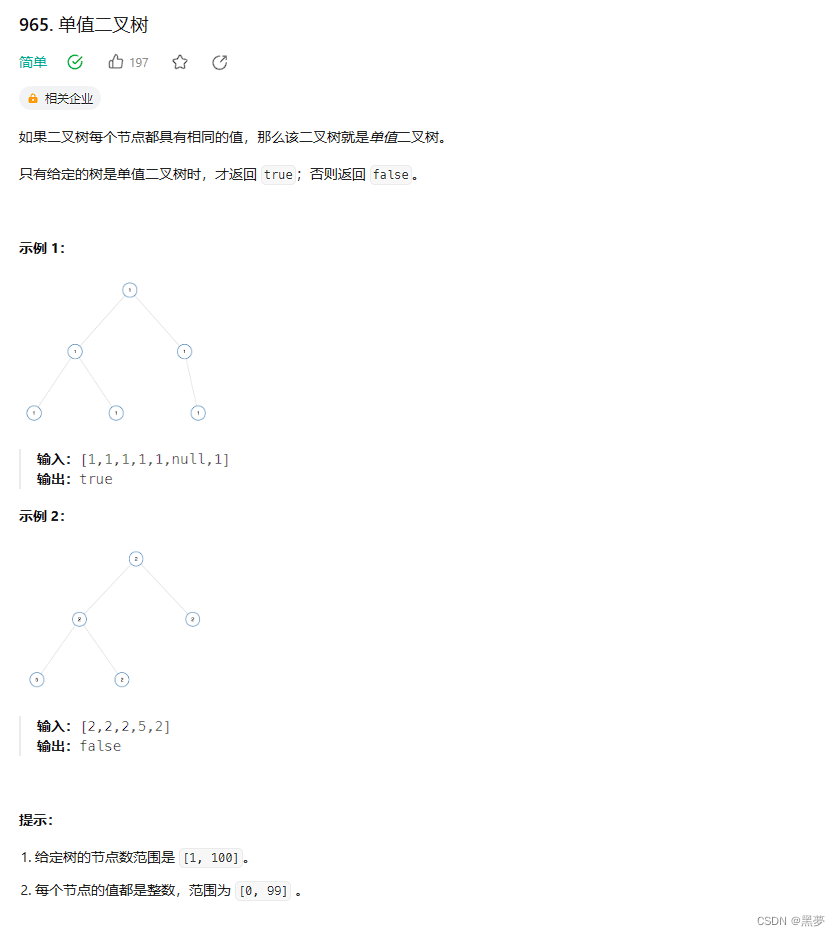
题一：单值二叉树

965. 单值二叉树 - 力扣（LeetCode）

思路一：

对整棵二叉树进行遍历比较！！！

第一步：优先判断树是否为空，空树为真；

第二步：判断左树是否存在且左树值等于根值，然后再判断右树存在且右树值等于根值;

第三步：最后,以当前为节点遍历左子树和右子树。

bool isUnivalTree(struct TreeNode* root)
{//判断子树是否为空if(root == NULL)return true;//左树存在且左树值等于根值if(root->left && root->left->val != root->val)return false;//右树存在且右树值等于根值if(root->right && root->right->val != root->val)return false;//递归判断子树值是否都相等return isUnivalTree(root->left) && isUnivalTree(root->right);
}

题二：二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）

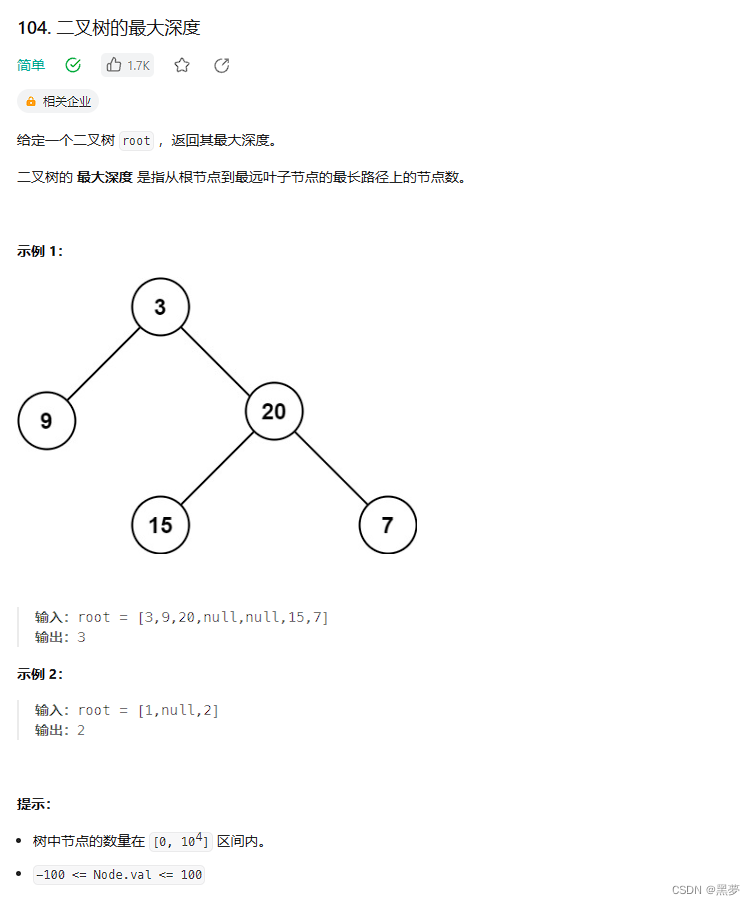
思路一：

第一步：判断树是否为空，为空返回0；

第二步：定义一个leftdeep：记录除根层以外左子树层数；定义一个rightdeep：记录除根层以右左子树层数；

第三步：当遍历到树的子节点 返回值最大的值+1(加上当前层).

int maxDepth(struct TreeNode* root)
{   if(root == NULL)return 0;//记录除根层以外左子树层数int leftdeep = maxDepth(root->left);//记录除根层以外右子树层数int rightdeep = maxDepth(root->right);return leftdeep > rightdeep ? leftdeep+1 : rightdeep+1;
}