数学与经济管理（2-4分）

章节概述

最小生成树问题

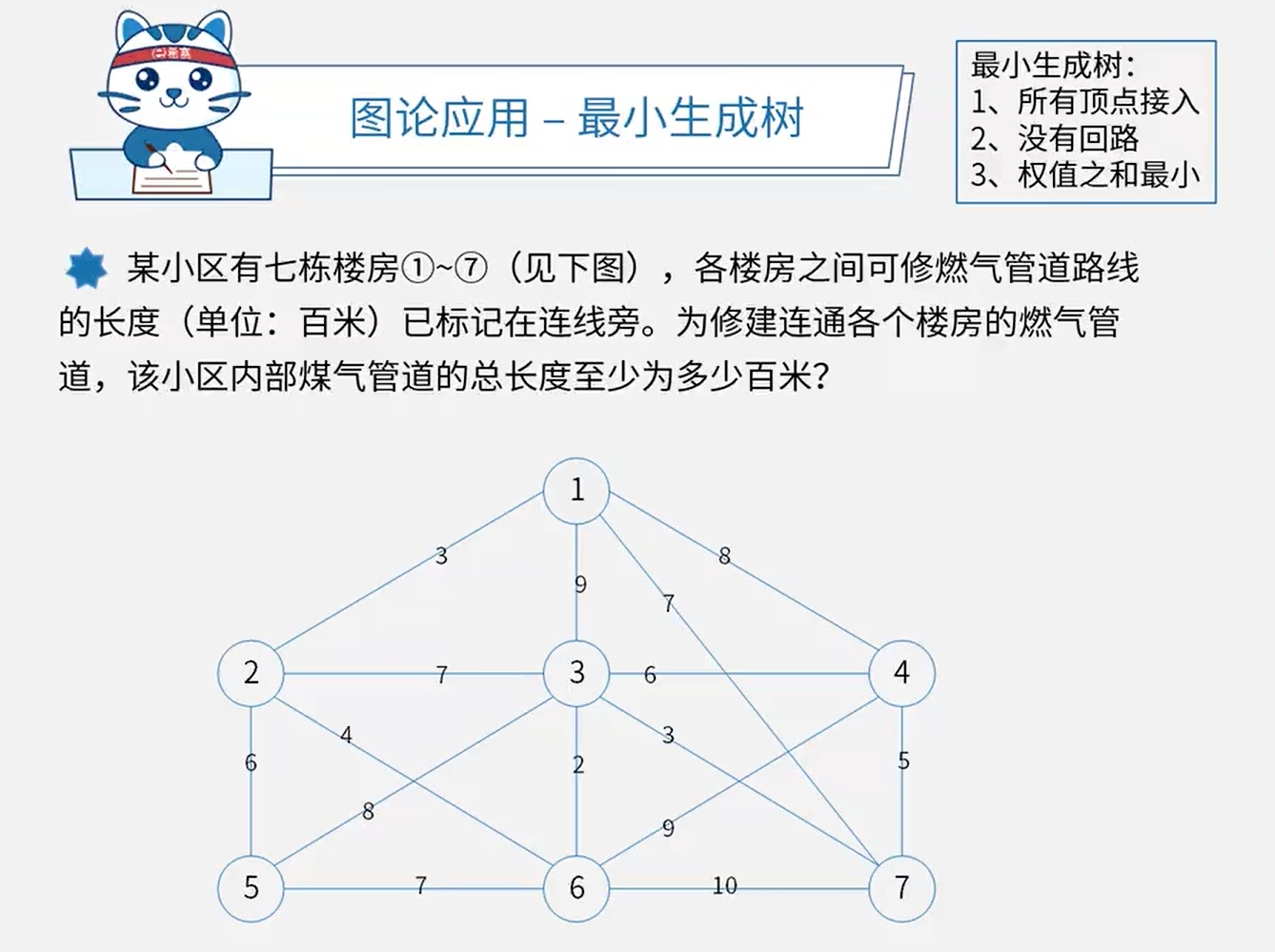
答案：23

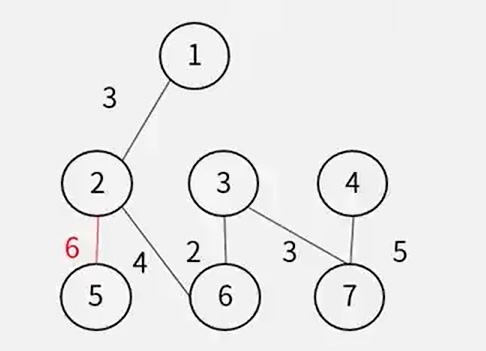
讲解地址：74-最小生成树问题_哔哩哔哩_bilibili

最短路径问题

答案：81

讲解地址：75-最短路径问题_哔哩哔哩_bilibili

网络与最大流量问题

真题

讲解地址：76-网络与最大流量问题_哔哩哔哩_bilibili

真题

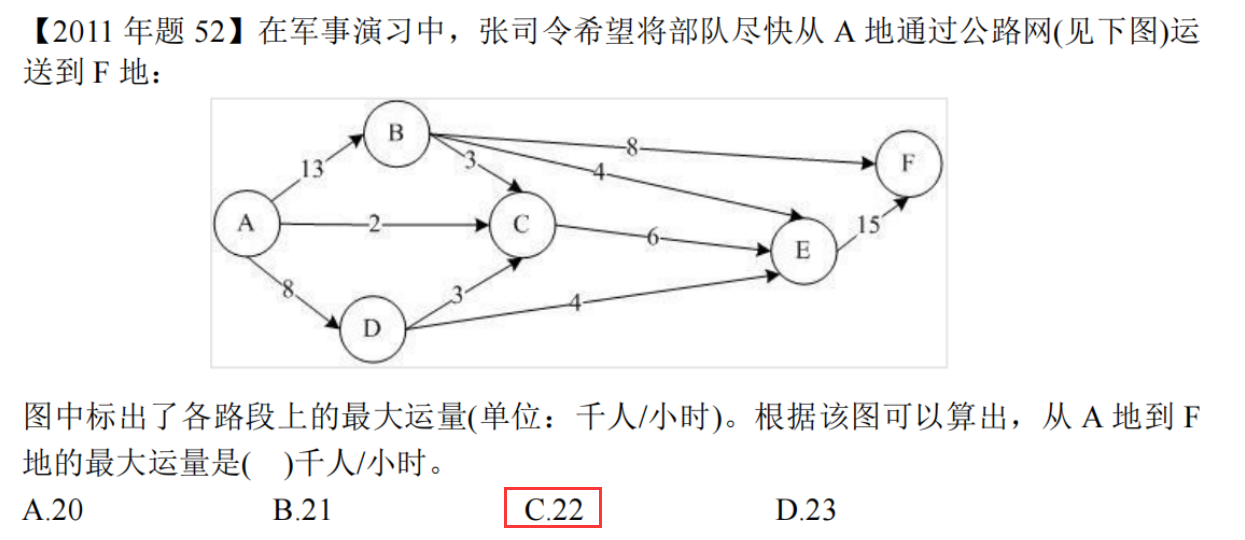
讲解地址：76-网络与最大流量问题_哔哩哔哩_bilibili

线性规划

真题

真题

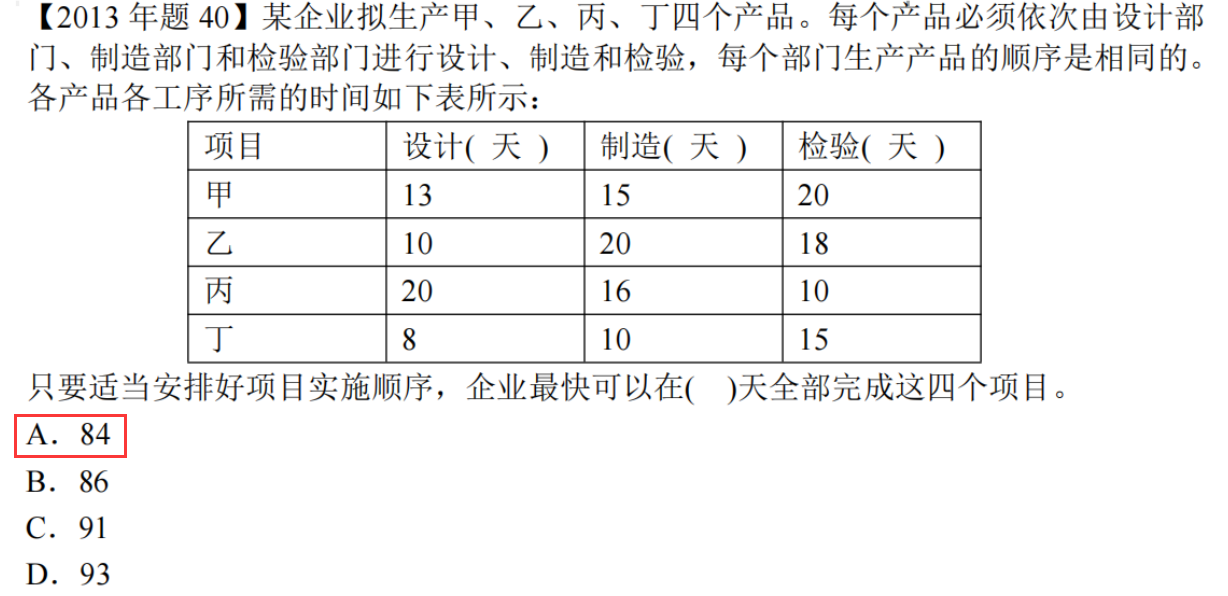
真题

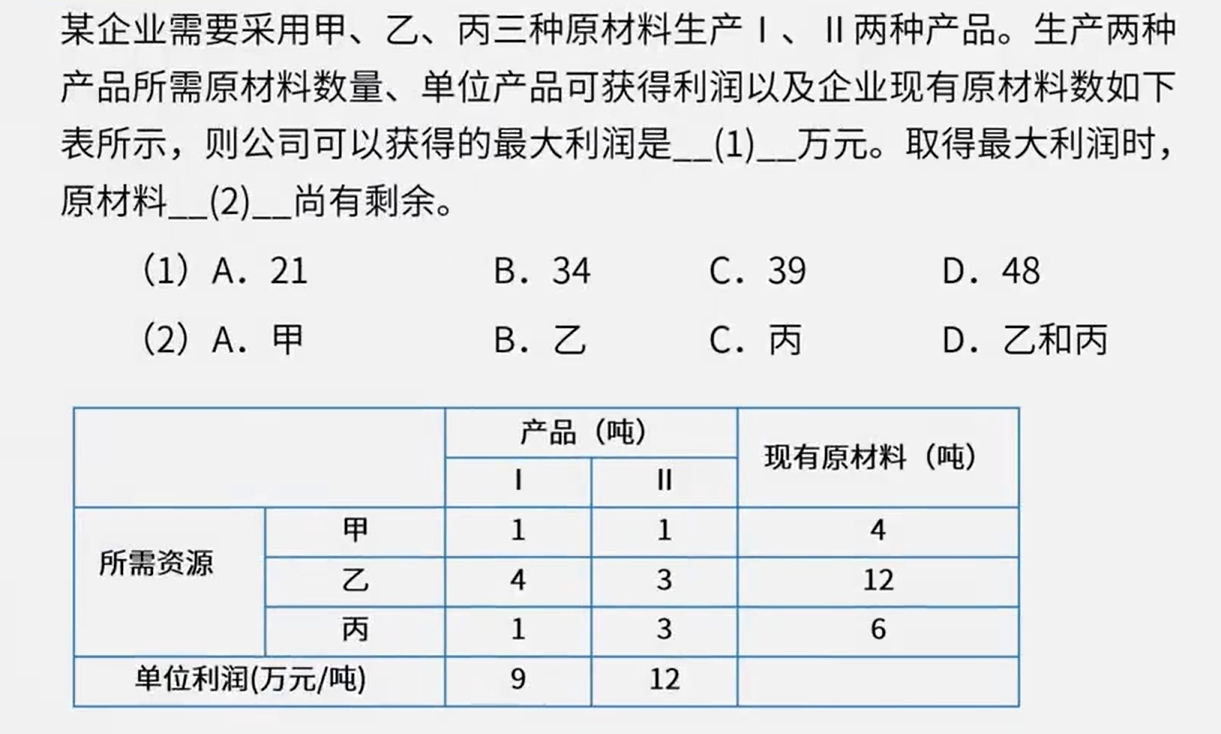
讲解地址：77-线性规划_哔哩哔哩_bilibili

真题

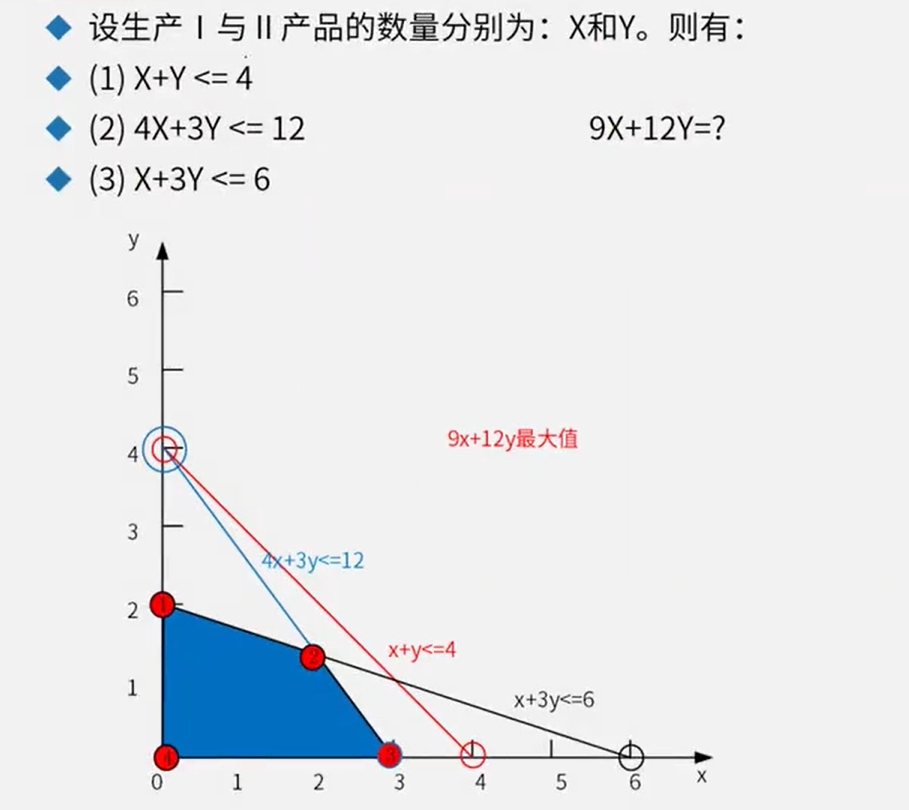
答案：34

真题

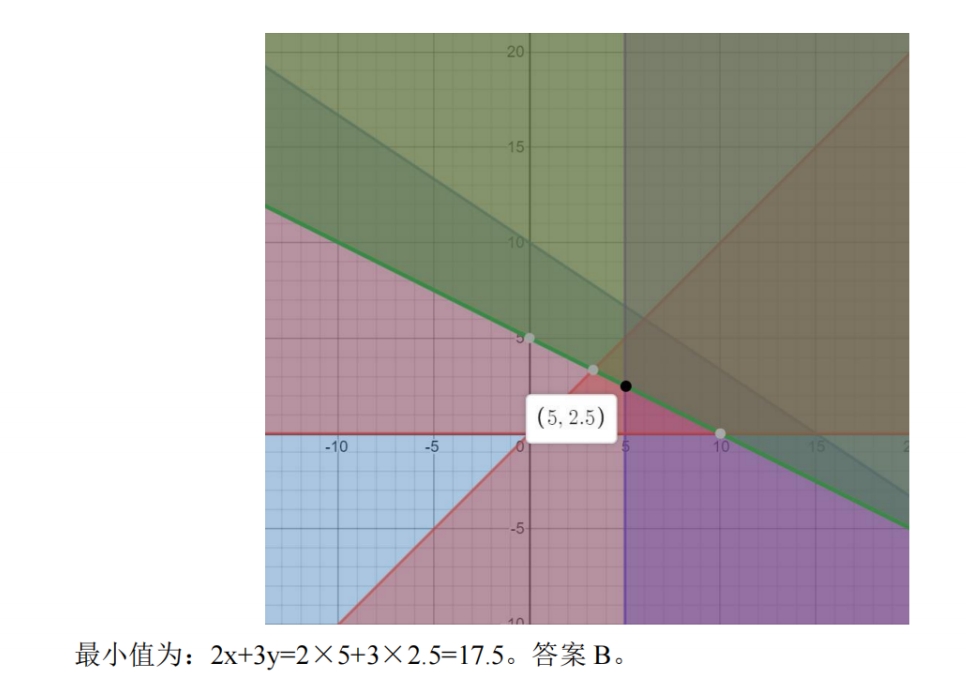
暴力出奇迹（动态规划）

真题

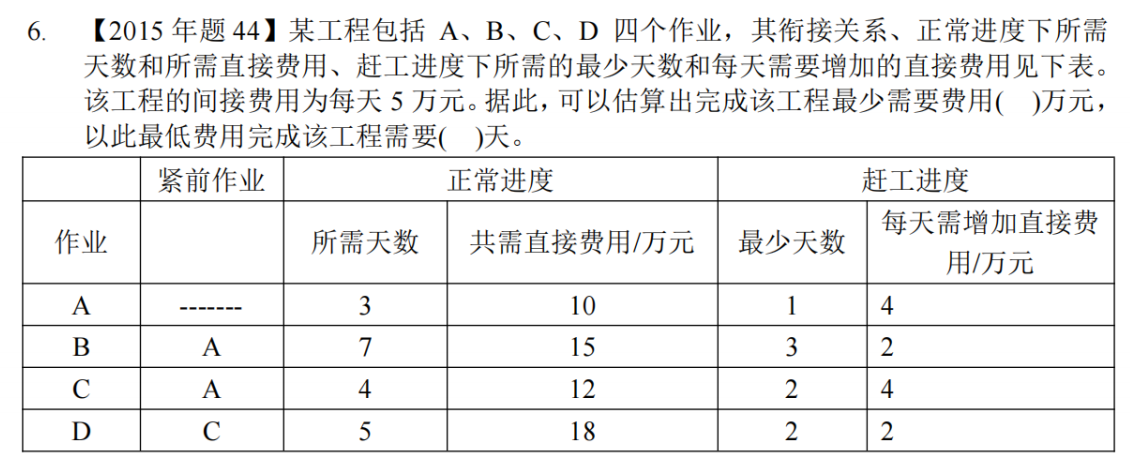
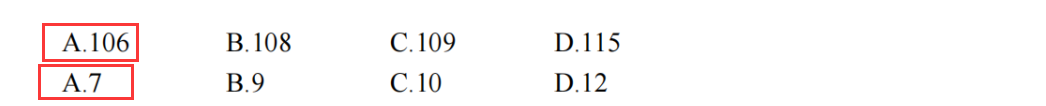
真题

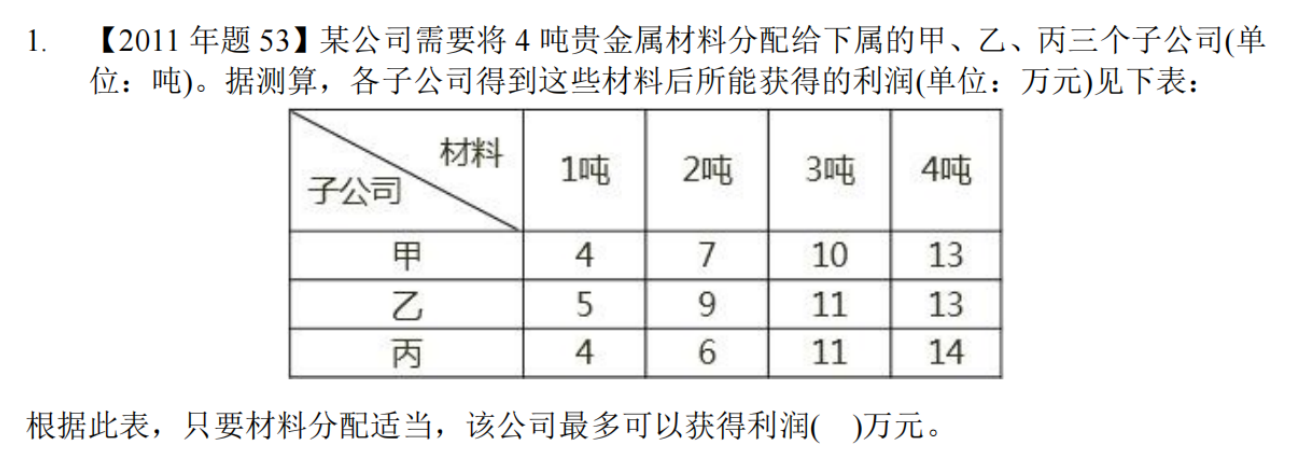
答案：17万

骚戴理解：这里我用的穷举法，一个个列出来，这个方法是最笨最容易出错的，但是是最简单的方法，同时注意在穷举的时候融入控制变量法的思想

真题

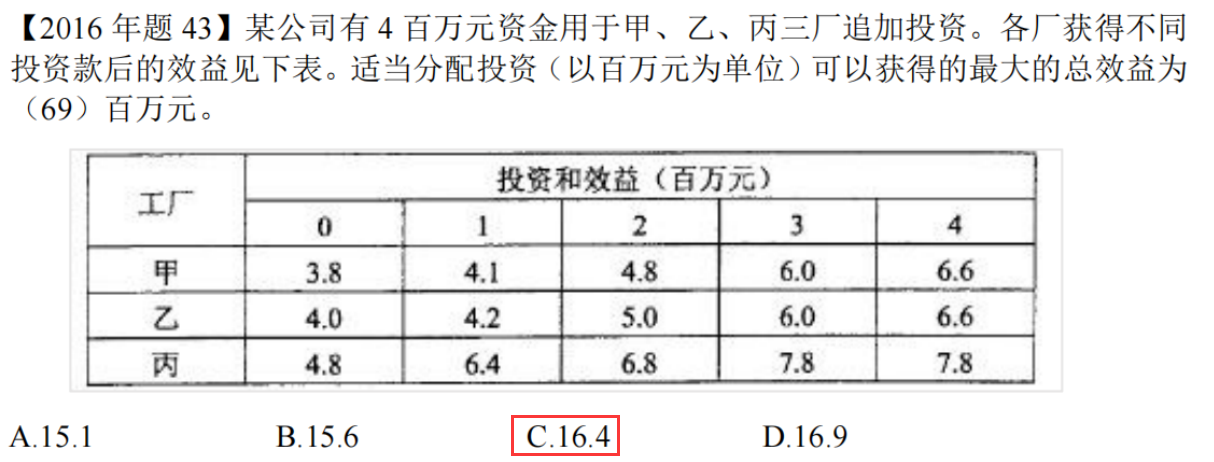
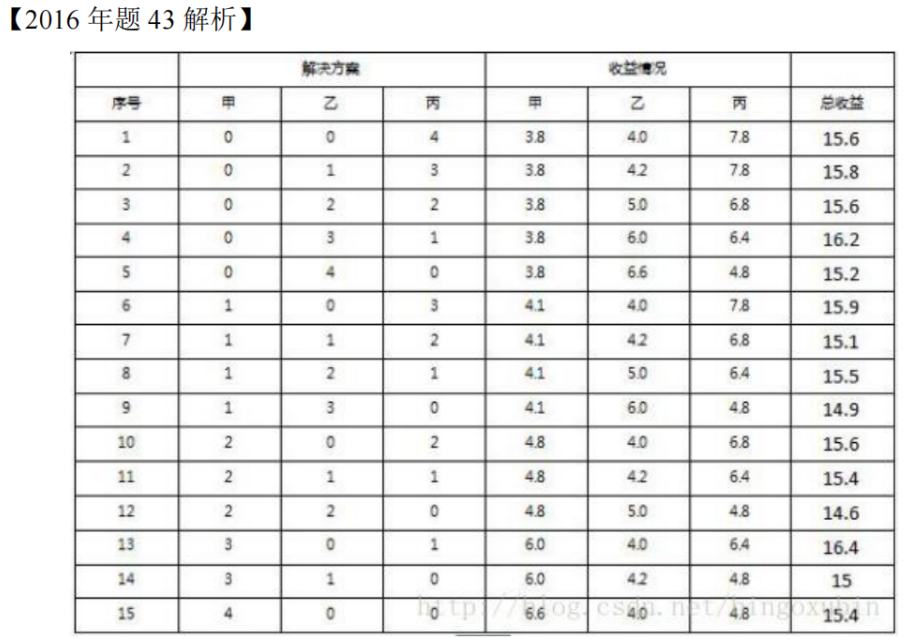
真题

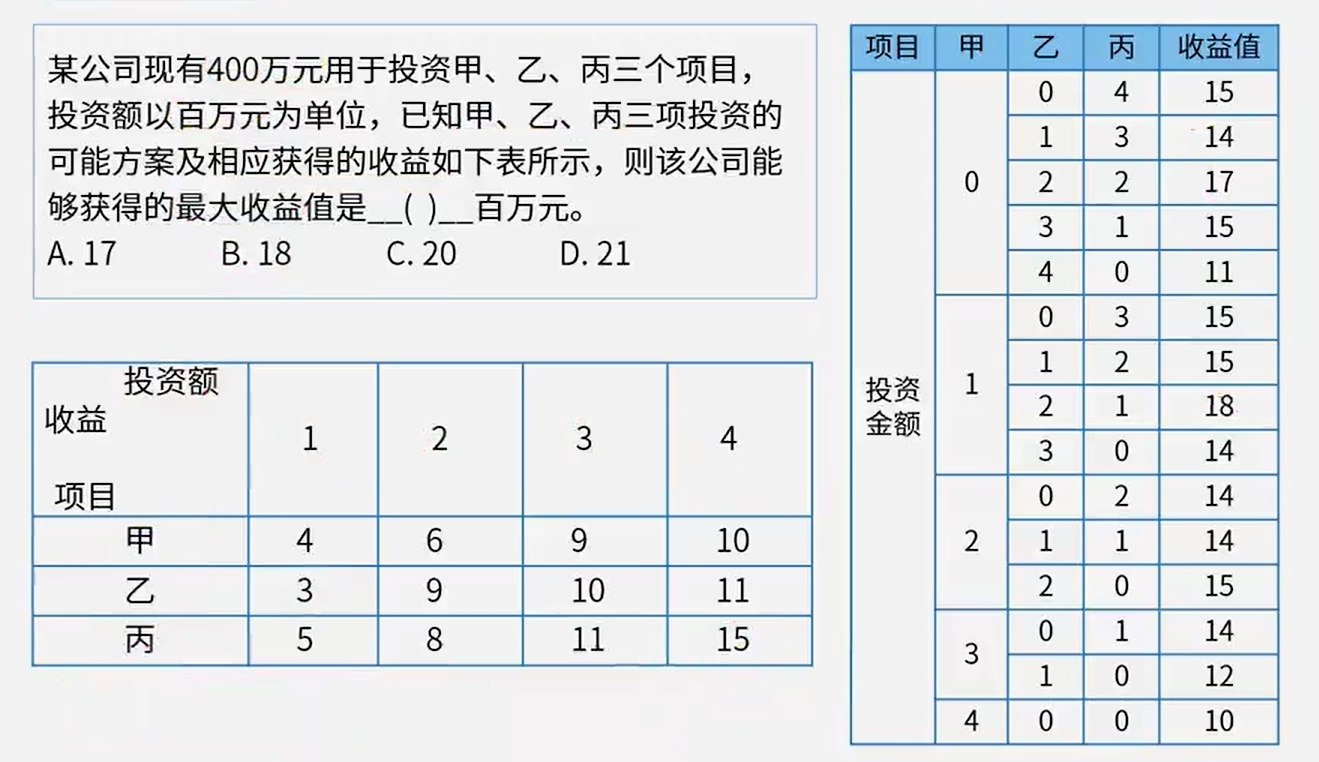
答案：B

骚戴理解：这个地方采用的就是暴力破解，把甲乙丙三种组合一个个列举出来，然后去计算总收益

讲解地址：78-动态规划_哔哩哔哩_bilibili

真题

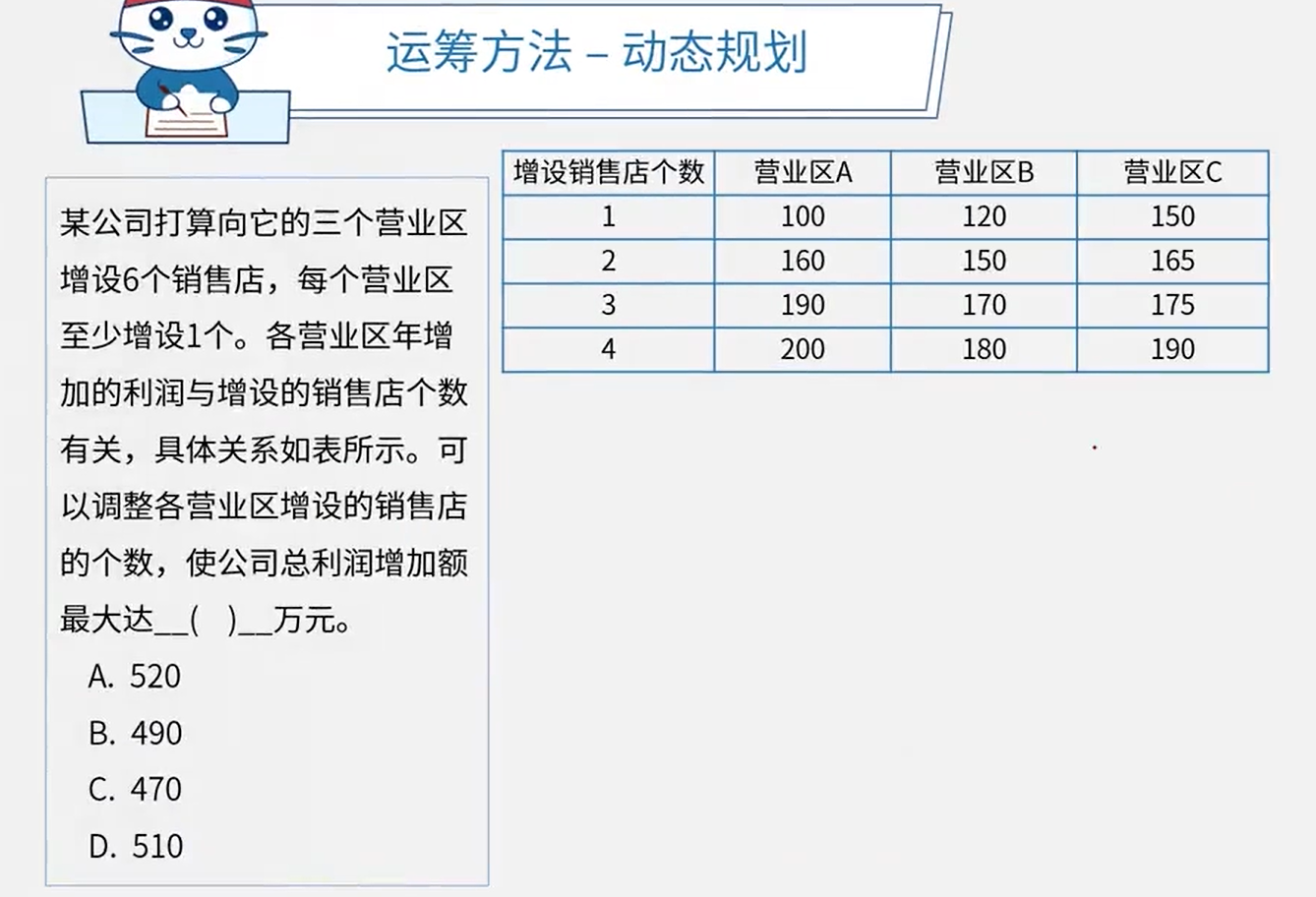
答案：B

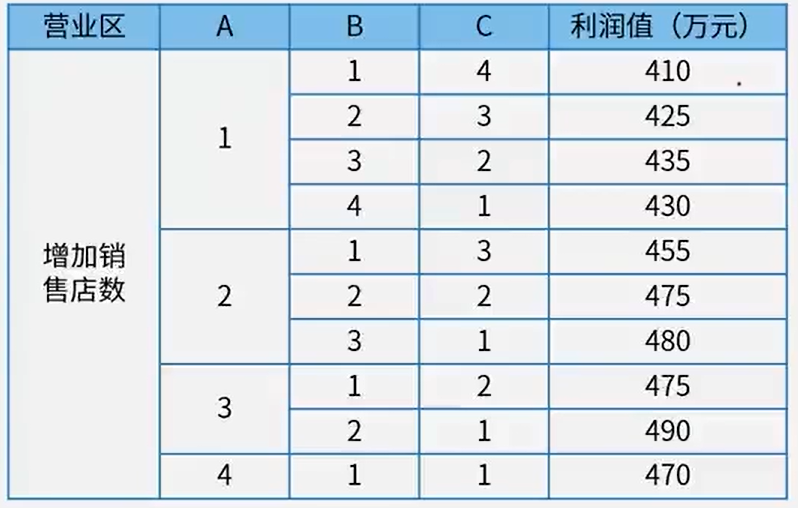
讲解地址：78-动态规划_哔哩哔哩_bilibili

真题

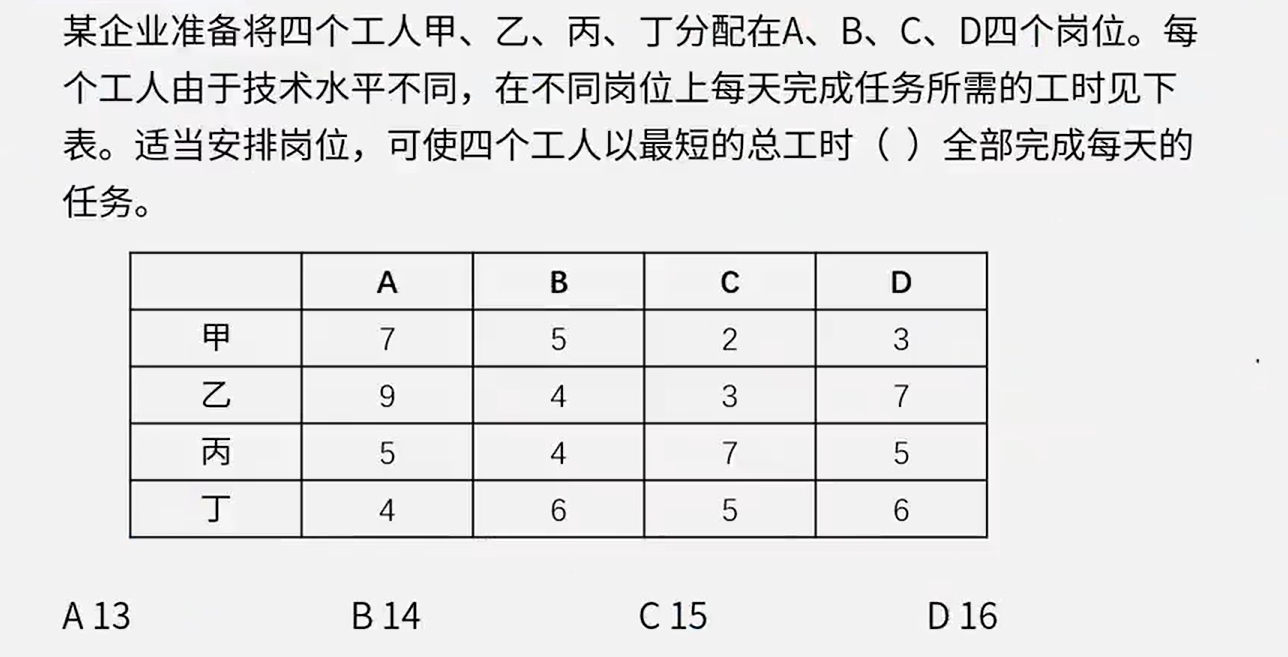
答案：B

讲解地址：78-动态规划_哔哩哔哩_bilibili

矩阵化简

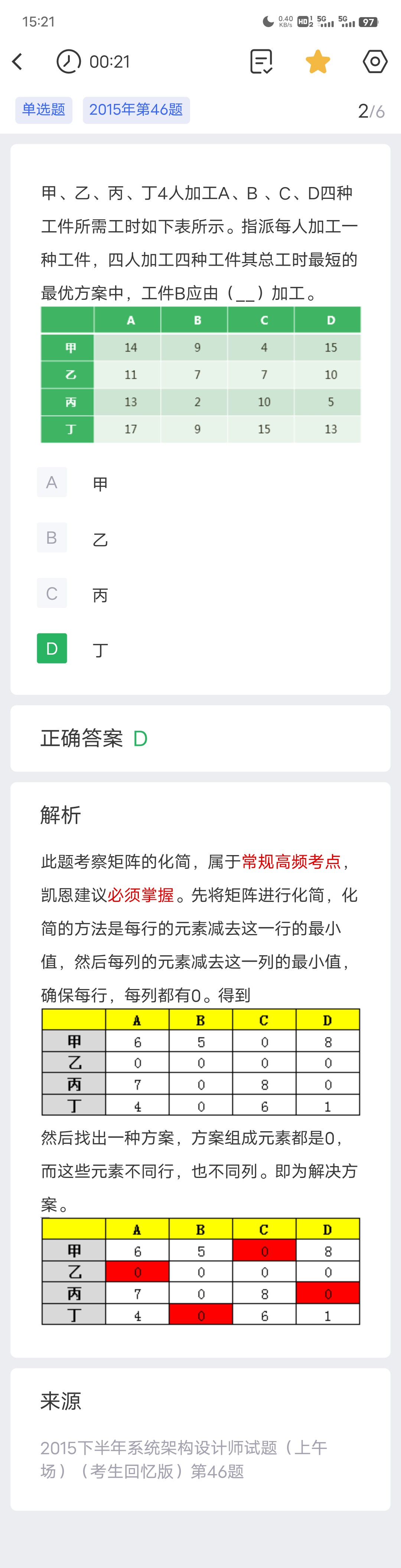
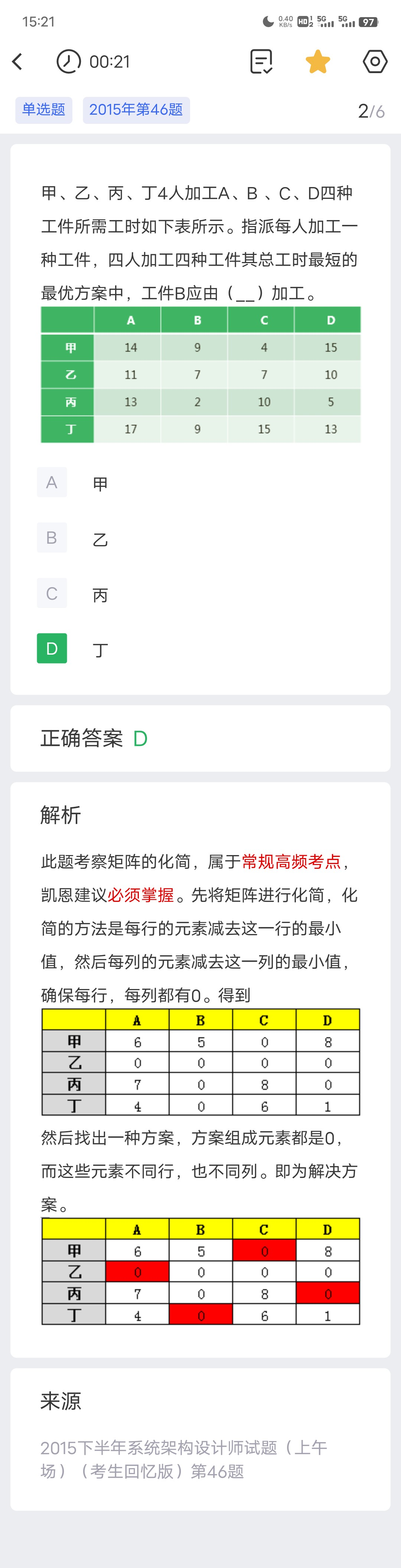
真题

真题

排队论

答案：C

讲解地址：79-排队论_哔哩哔哩_bilibili

博弈论

真题

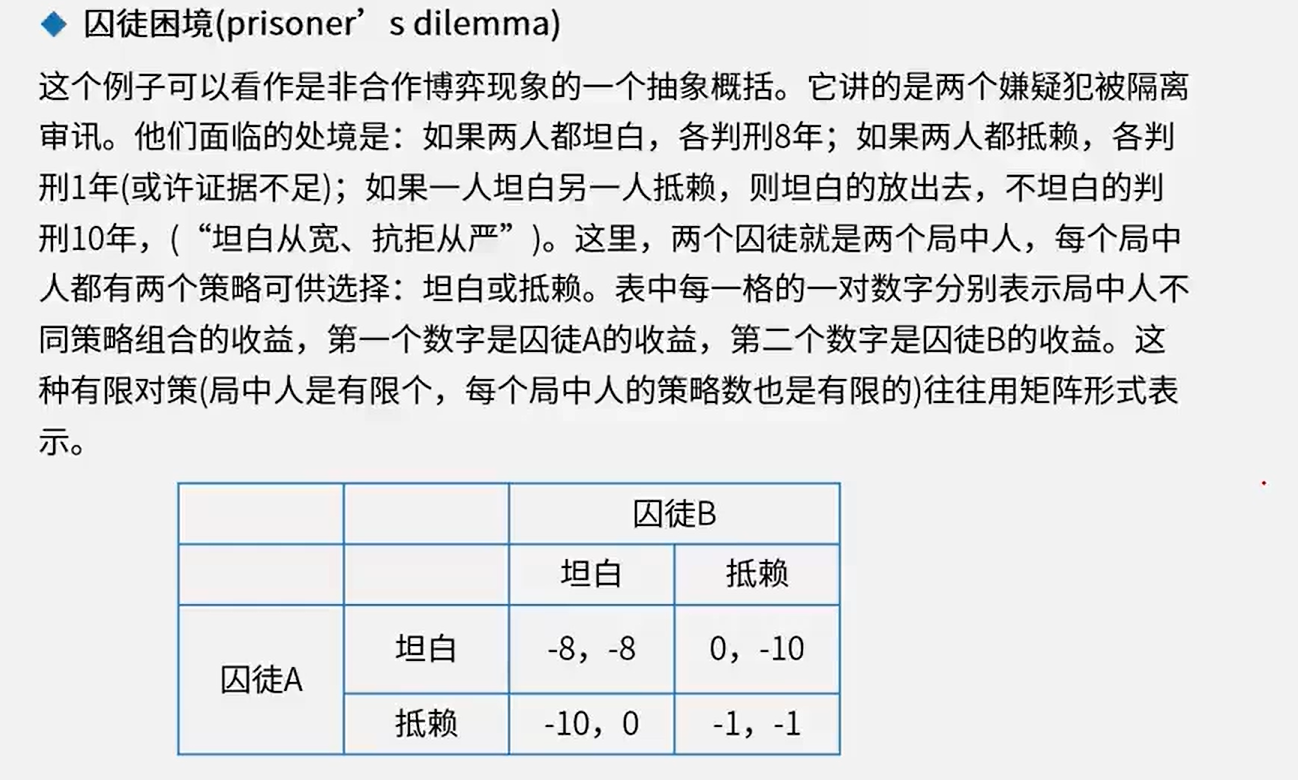
答案：囚犯A坦白，囚犯B抵赖

讲解地址：80-博弈论_哔哩哔哩_bilibili

真题

答案：甲选择低价，乙选择低价

骚戴理解：这里别搞混淆了，每一栏的两个数字分别代表甲的收益和乙的收益，首先捋清楚这一点，这样的题目很容易晕的

讲解地址：80-博弈论_哔哩哔哩_bilibili

状态转移矩阵

真题

真题

答案：C

骚戴理解：首先注意这个地方要算两次，因为是两个月以后，其次注意这里可以套用数学公式

讲解地址：81-状态转移矩阵_哔哩哔哩_bilibili

真题

答案：D

讲解地址：81-状态转移矩阵_哔哩哔哩_bilibili

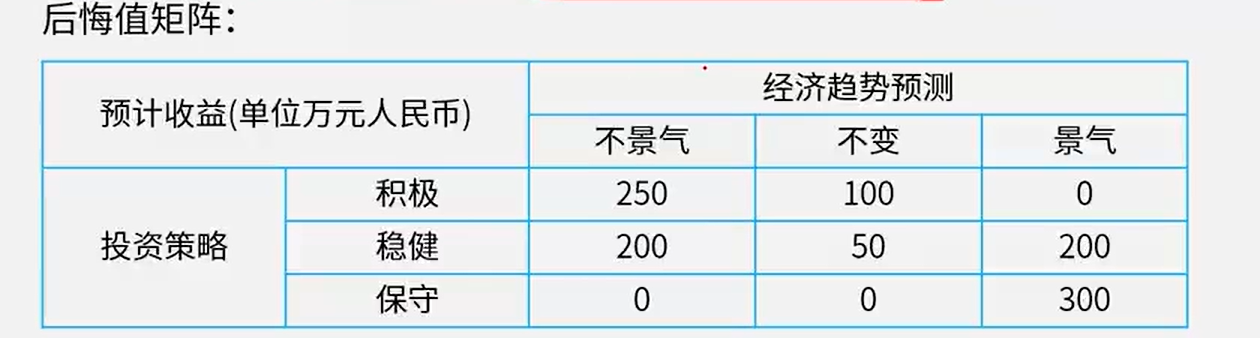
不确定型决策

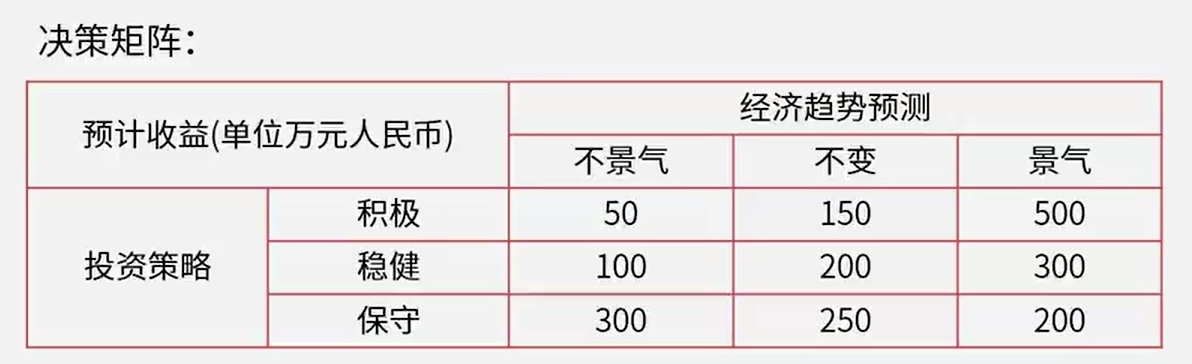
骚戴理解：

• 如果上面的决策矩阵采用乐观主义准则（大中取大），那就从每个策略的最大值中取最大值，也就是【500,300,300】，即取500，，所以选择积极策略
• 如果是悲观准则（小中取大），那就从每个策略的最小值中取最大值，也就是【50,100,200】中的最大值，即取200，所以选择保守策略
• 如果是等可能准则，那就要计算了，三种策略对应的计算公式如下所示，可以看到，其实最终也就是把这些值加起来看看谁最大就选谁，也就是【700,600,750】，所以选择保守策略

• • 积极：（50+150+500）*（1/3）= 700 *（1/3）
  • 稳健：（100+200+300）*（1/3） = 600 *（1/3）
  • 保守：（300+250+200）*（1/3） = 750 *（1/3）

• 如果是后悔准则（最大后悔值选最小），那么需要还出下面的这个后悔值矩阵才行，然后在这个矩阵里面的最大后悔值中选最小值，然后从策略的角度来看，也就是【250,200,300】中取最小值，即取200，所以选择稳健策略，那这个后悔值怎么得出来的呢？这个后悔值其实就是一列列的看，然后取最大的值作为基础，计算其他的和这个基数的差值，差值就是后悔值，例如不景气这一列，最大值为300，那就是基数为300，然后其他的和基础的差值分别为250和200，那这些值就是对应的后悔值

讲解地址：82-不确定型决策_哔哩哔哩_bilibili

决策表与决策树

决策树

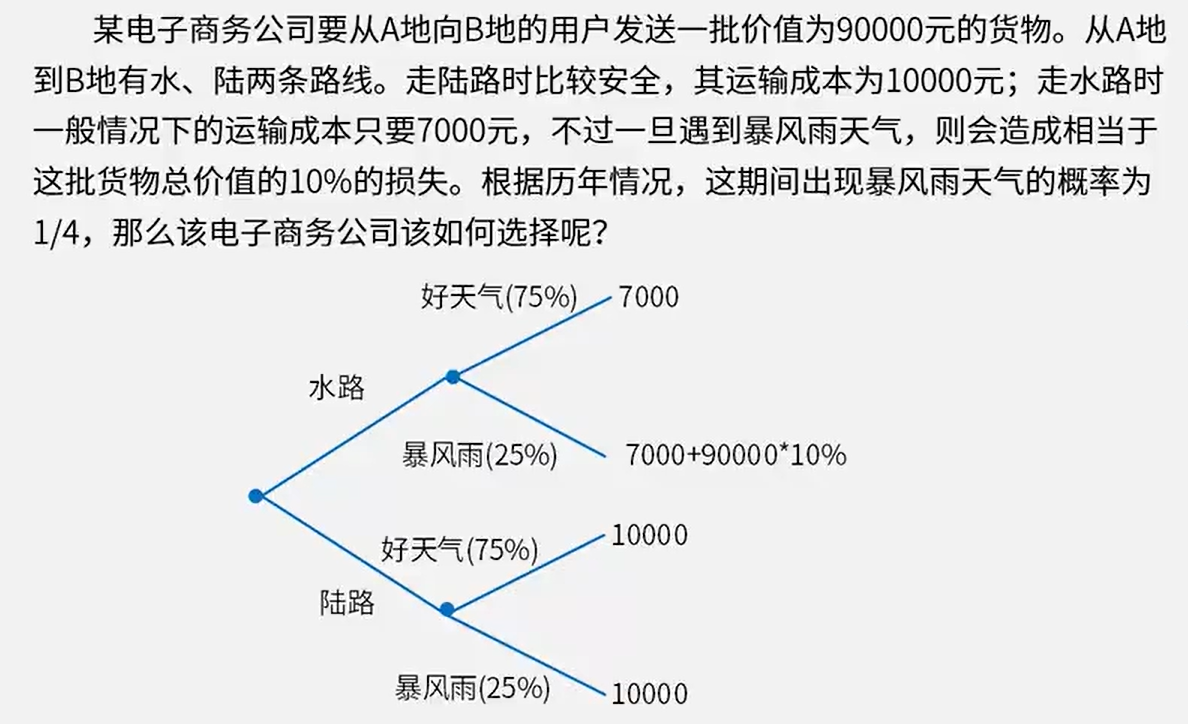
答案：水路

骚戴理解：这个题目首先会根据题目画出决策树，因为有的题目可能不给决策树，要自己画，其次就是要会求加权平均值，然后根据题目需求来决定是取最小值还是最大值，这里算的是成本，所以要取最小值，例如上面的这个题目的加权平均值如下所求

• 水路：7000*0.75+（7000+90000*10%）*0.25=9250
• 陆路：10000*0.75+10000*0.25 = 10000

决策表

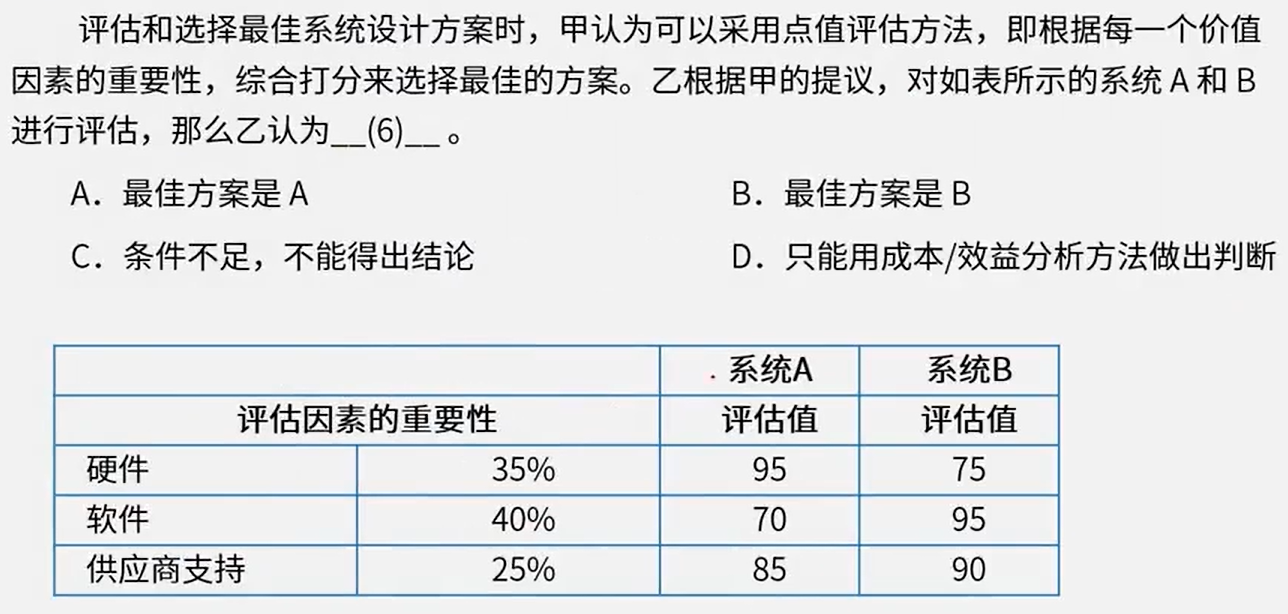
答案：B

骚戴理解：这个就跟简单了，也是求加权平均值，然后根据题目需求来决定是取最小值还是最大值，这里是求价值，那自然是取最大值

• A系统：95*35%+70*40%+85*25%=82.5
• B系统：75*35%+95*40%+90*25%=86.75

真题

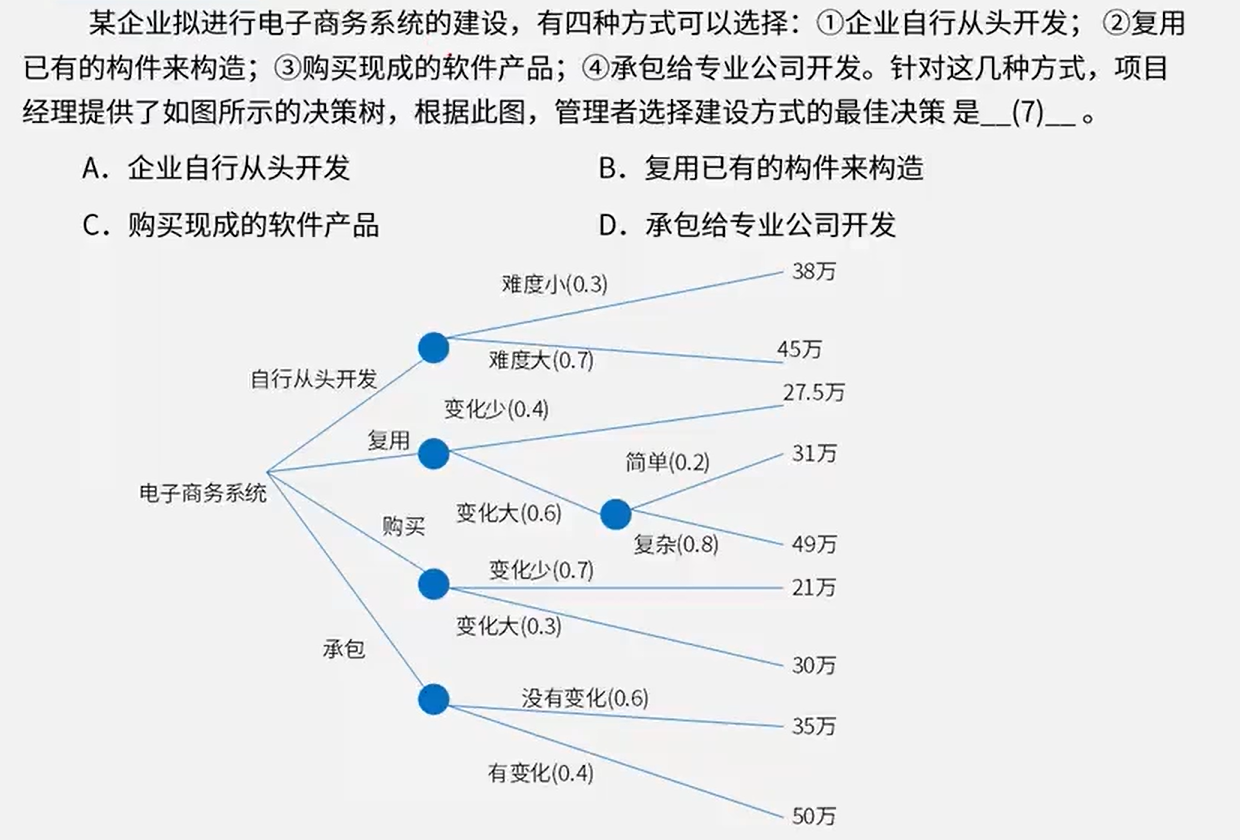
答案：C

骚戴理解：这个题目也一样是求加权平均值的，只是复用那里多了一个分支，这种情况用乘法即可，例如复用的情况计算加权平均值的公式：0.4*27.5+（0.6*0.2*31+0.6*0.8*49）=11+（3.72+23.52）=38.24

真题

答案：B

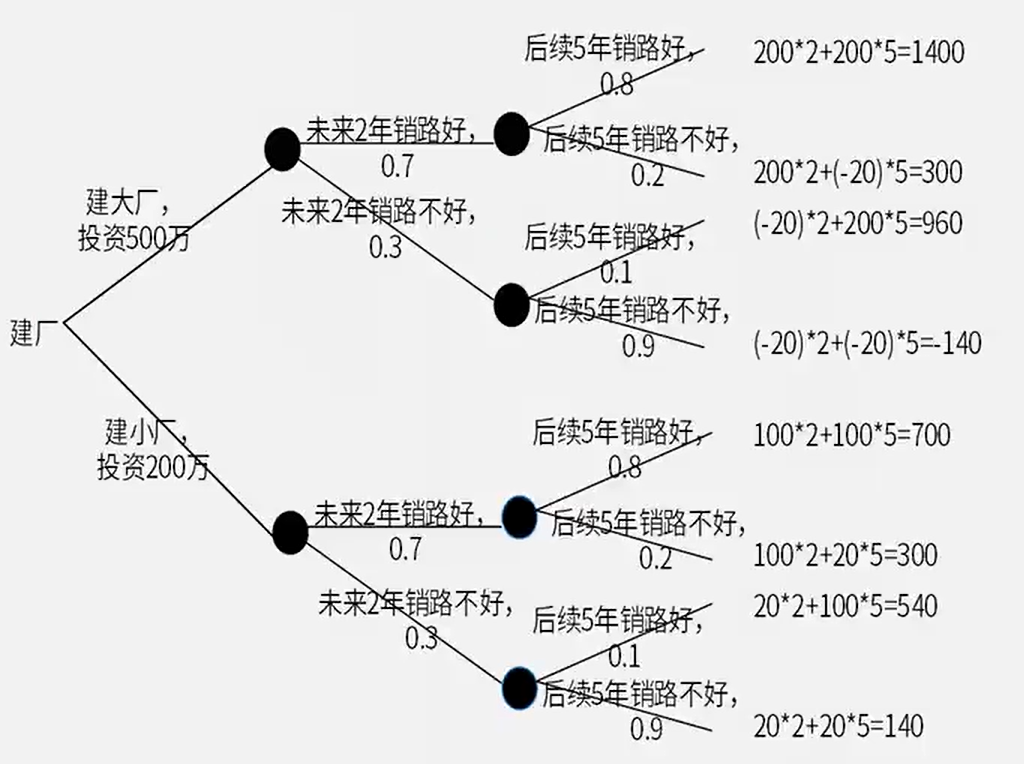
讲解地址：83-决策表与决策树_哔哩哔哩_bilibili

数学建模

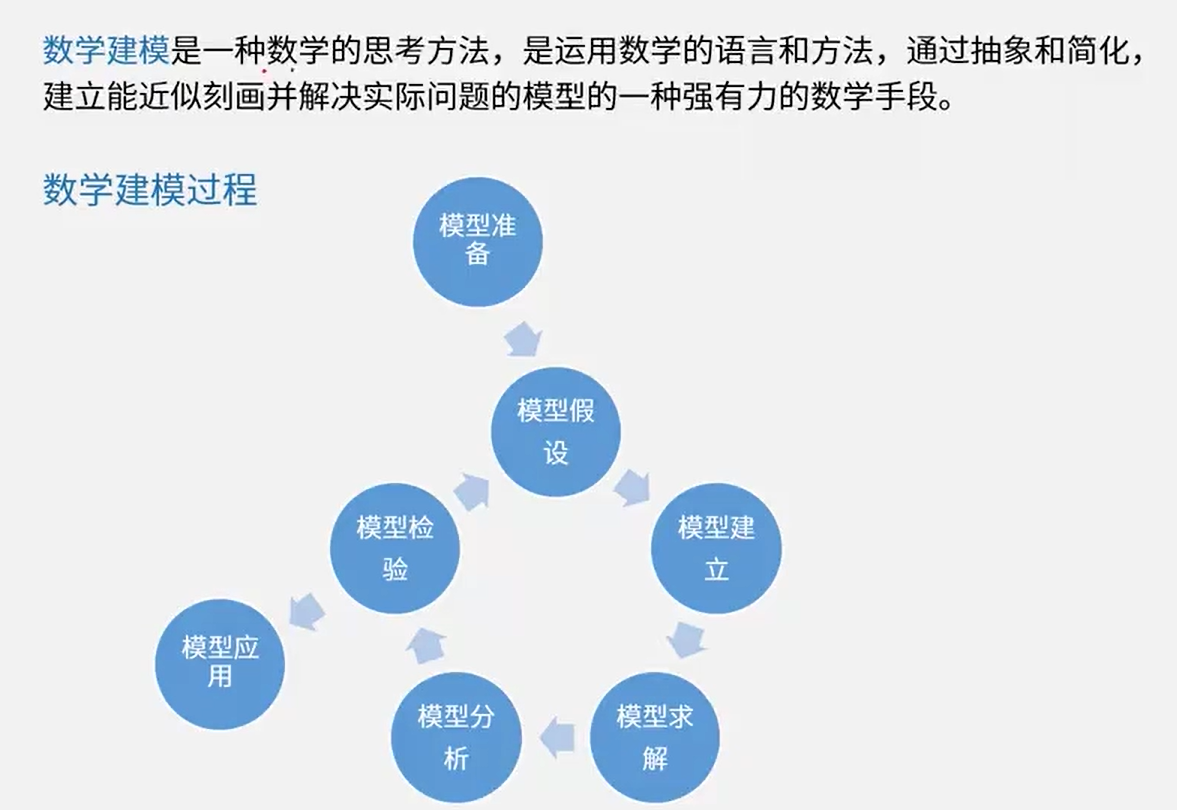
建模过程

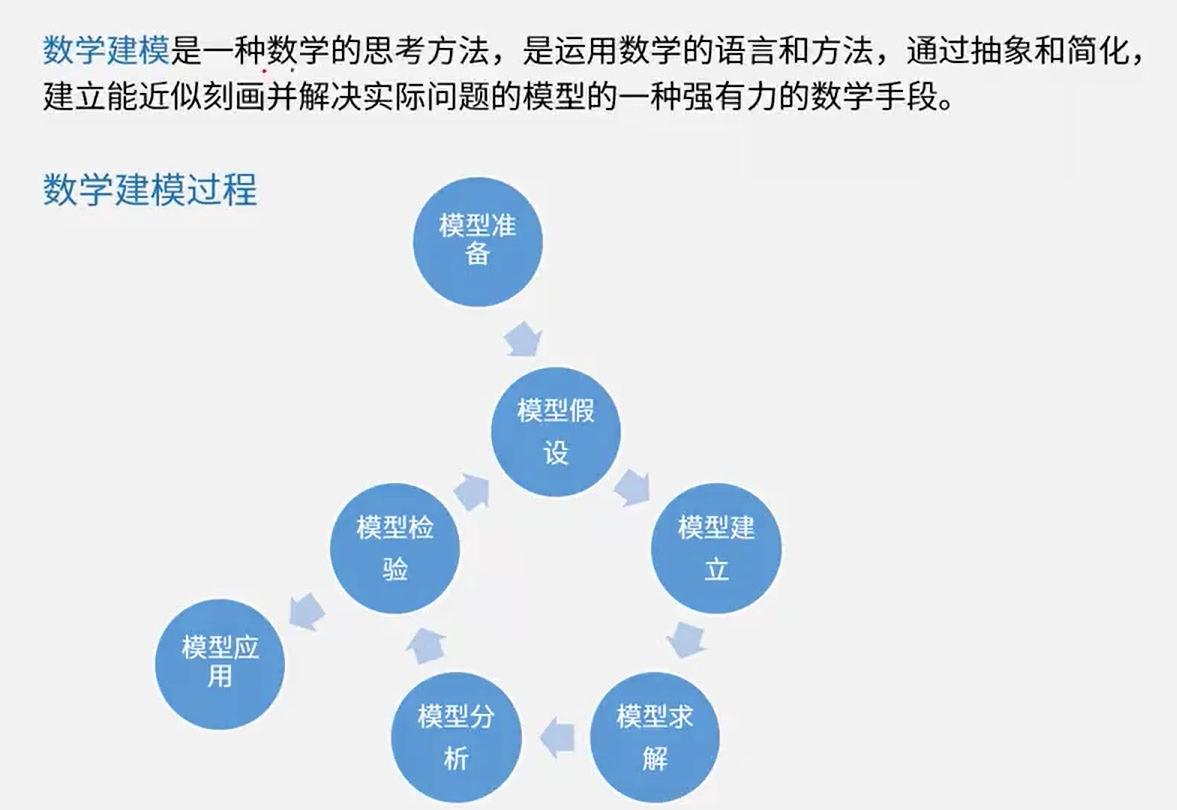
模型分析

模型校验

建模方法

真题

真题

答案：C

真题

答案：D

讲解地址：84-数学建模_哔哩哔哩_bilibili

无家可归

真题

真题

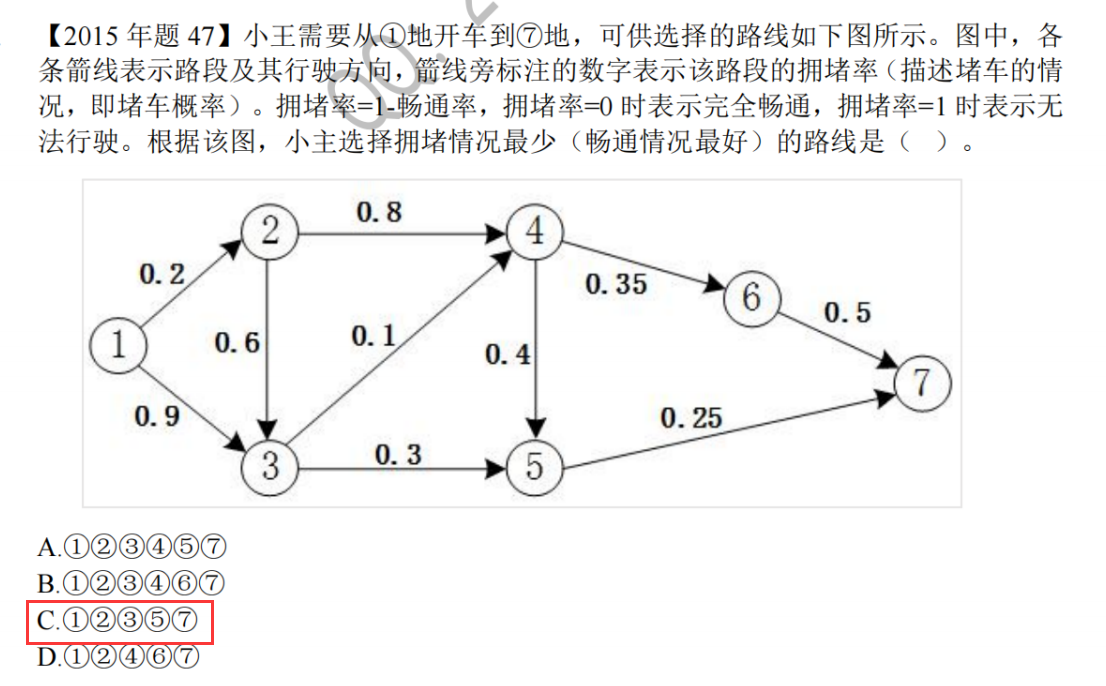
真题

真题

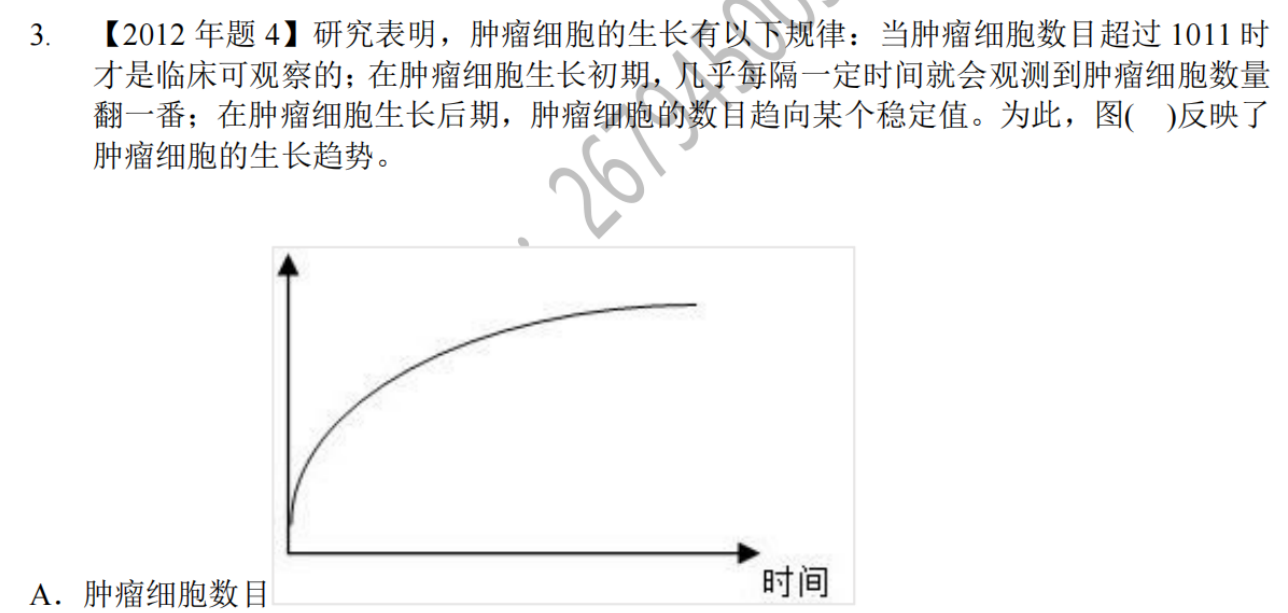
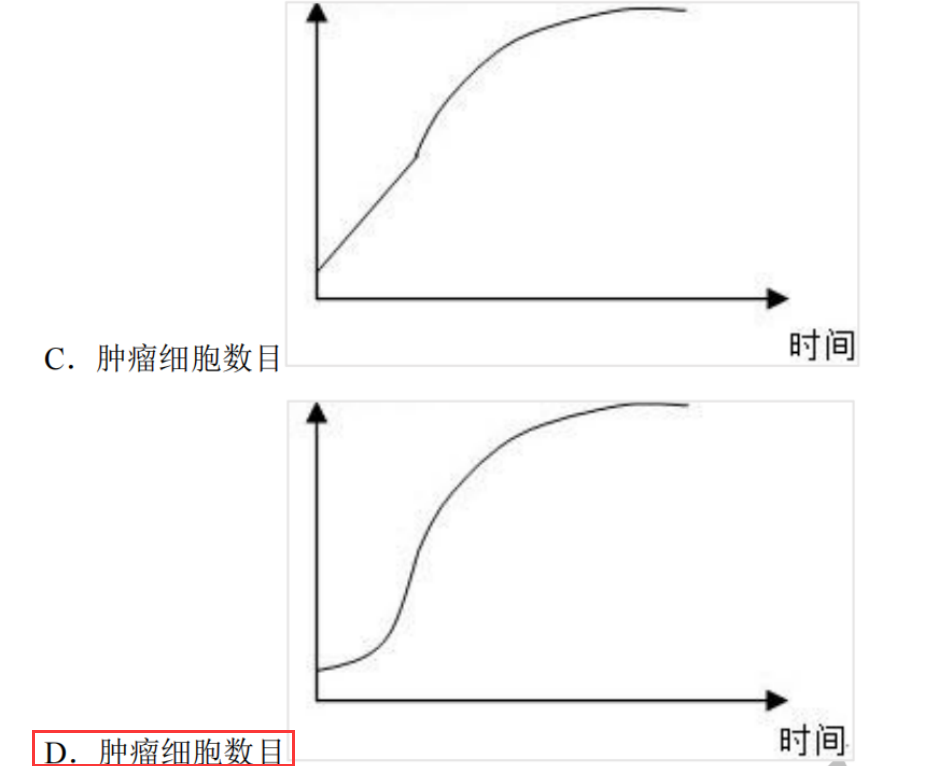
真题

真题

解析

此题考察蒙特卡洛算法的相关应用，属于常规高频考点。蒙特卡罗方法是一种统计模拟方法，其思想核心是通过模拟大量样本集或随机过程来近似实际问题对象。其名字来源于蒙特卡罗赌城，最初应用于20世纪40年代美国的曼哈顿原子弹计划，如今在数据分析和机器学习领域中有广泛的应用。蒙特卡罗方法的三个典型应用场景:近似计算不规则面积/体积/积分、模拟随机过程预测可能性结果区间范围、利用接受-拒绝采样进行对分布未知参数的统计推断

真题

真题

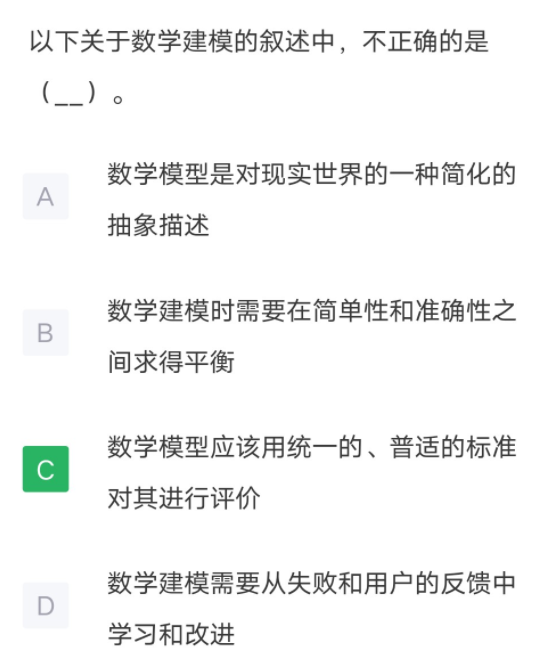
解析

此题考察数学建模的概念和特点，属于超纲低频考点。数学建模是利用数学方法解决实际问题的一种实践。数学建模的过程包括抽象、简化、假设、引入变量等步骤，建立数学模型，然后用先进的数学方法和计算机技术求解。数学模型是对于现实世界的一个特定对象、一个特定目的，根据特有的内在规律，作出一些必要的假设，运用适当的数学工具得到一个数学结构。对不同的问题，有不同的评价标准，数学模型难有统一的普适标准来评价。

真题