【期中复习】深度学习

文章目录

    • 机器（深度）学习的四大核心要素
    • 为什么深度学习，不增加网络宽度
    • 黑盒模型的问题
    • 计算图
    • 线性神经网络
    • 梯度下降
    • 学习率
    • 优化方法
    • softmax函数用于多分类
    • 交叉熵
    • 线性回归与softmax回归的对比
    • 为什么需要非线性激活函数
    • 感知机
    • 线性回归、softmax回归、感知机和支持向量机的比较
    • sigmoid激活函数
    • 双曲正切（tanh）激活函数
    • 线性（ReLU）修正函数
    • MLP
    • K折交叉验证
    • 估计模型的复杂度
    • 数据复杂度
    • 欠拟合和过拟合
    • 欠拟合和过拟合的原因
    • 正则化
    • Dropout
    • 梯度爆炸和梯度消失
    • 权重初始化
    • 参数初始化

机器（深度）学习的四大核心要素

数据、模型、性能度量（目标函数）、优化方法

为什么深度学习，不增加网络宽度

  • 增加深度使得学习高层次、抽象特征成为可能
  • 相比于增加宽度，增加深度的学习效率更高。比如对于一些要学习的多项式函数，浅层网络需要指数增长的神经元个数，其拟合效果才能匹配上多项式增长的深层网络
    宽度的优点：增加宽度会增加模型的记忆能力

黑盒模型的问题

数据安全隐患、输出不可信、模型改进局限、模型应用局限

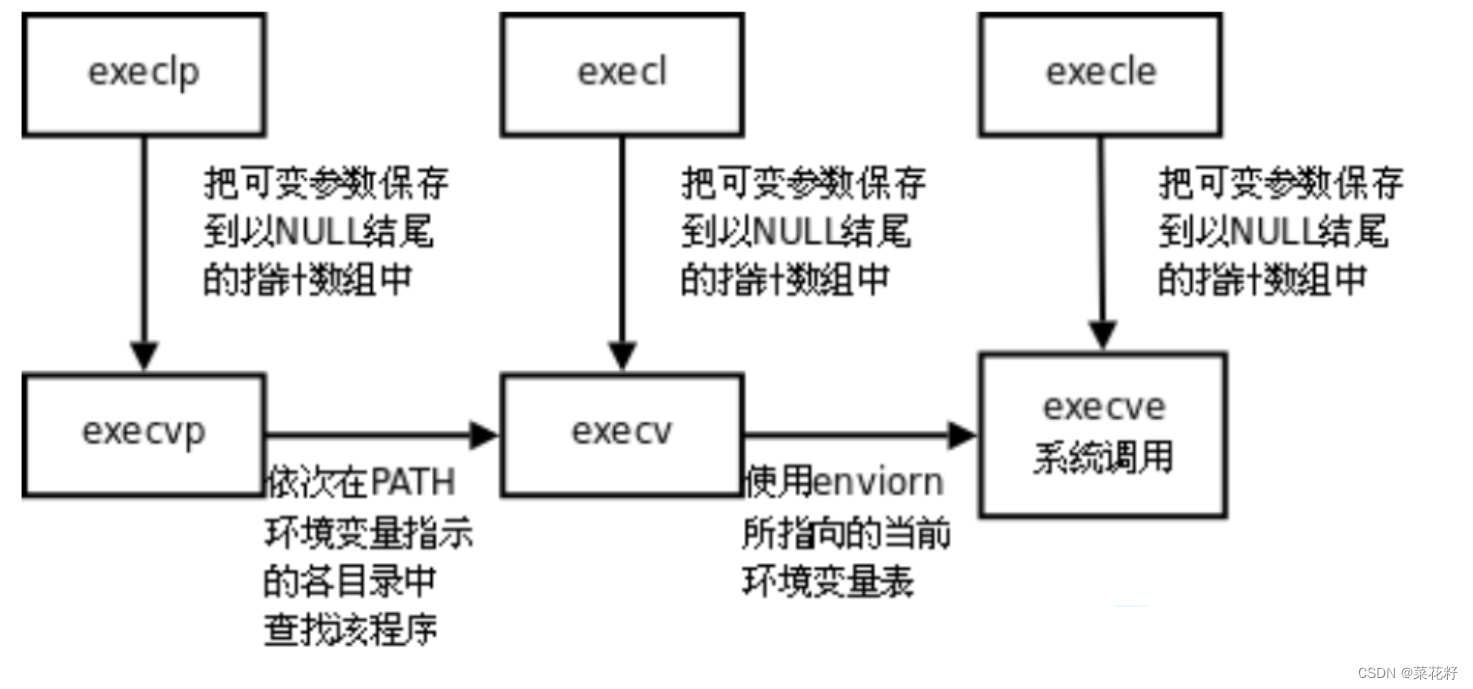
计算图

在这里插入图片描述

线性神经网络

  • 模型
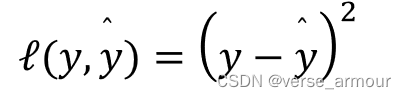
    在这里插入图片描述

  • 性能度量
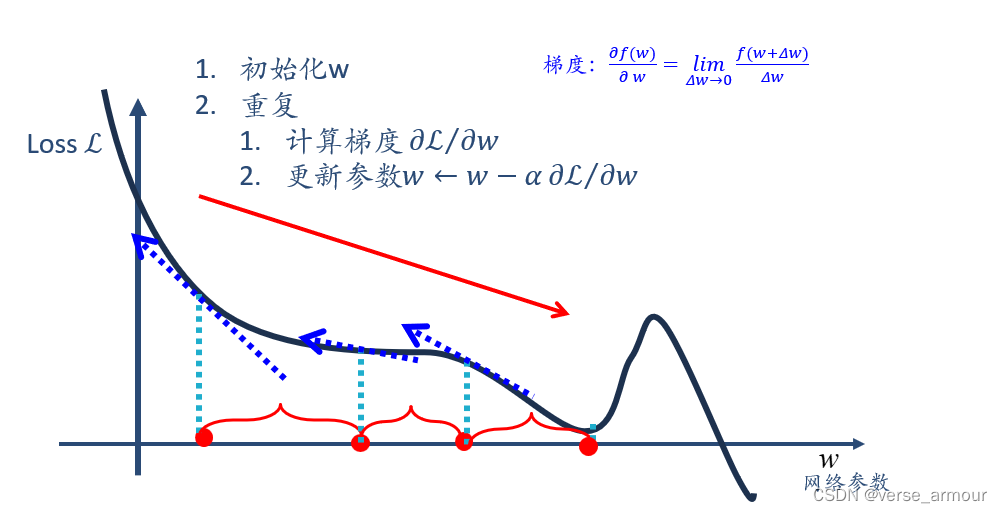
    在这里插入图片描述

  • 优化方法
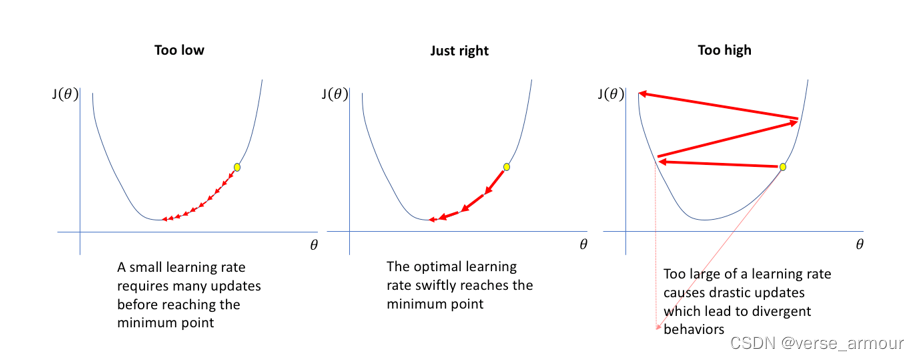
    在这里插入图片描述

梯度下降

在这里插入图片描述

学习率

在这里插入图片描述

优化方法

在这里插入图片描述

softmax函数用于多分类

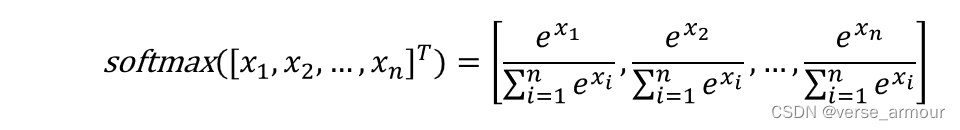
在这里插入图片描述

  • 可用：量化样本间的相对大小(等比例缩放不变)
  • 概率：每个样本取值范围[0,1],总和等于1
  • 可训练：可微分

交叉熵

在这里插入图片描述

线性回归与softmax回归的对比

在这里插入图片描述

为什么需要非线性激活函数

在这里插入图片描述
因为是线性的，神经网络虽然引入了隐藏层，却依然等价于一个单层神经网络

感知机

在这里插入图片描述
在这里插入图片描述

线性回归、softmax回归、感知机和支持向量机的比较

在这里插入图片描述

sigmoid激活函数

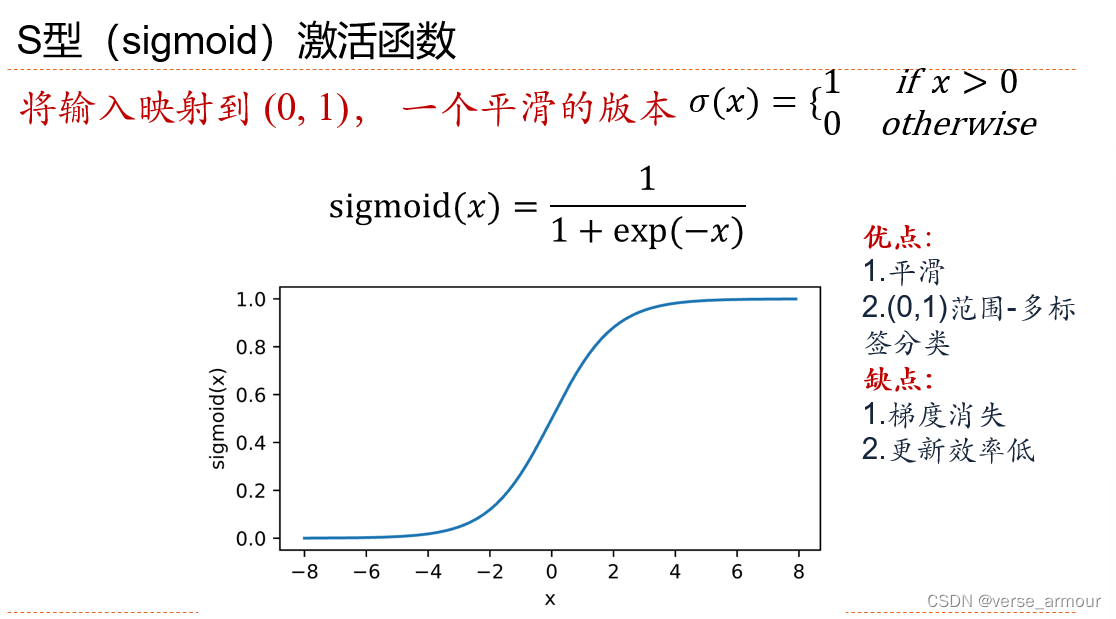
在这里插入图片描述

  • 优点
    （0-1），平滑、多标签分类
  • 缺点
    梯度消失、更新效率低

双曲正切（tanh）激活函数

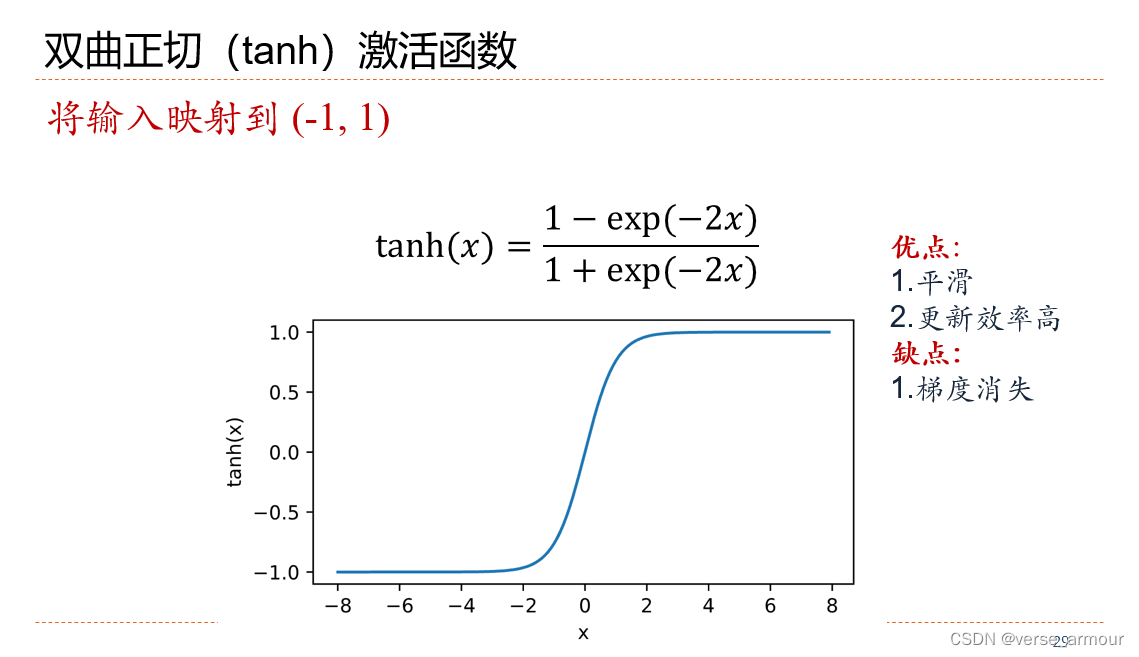
在这里插入图片描述

  • 优点
    （-1，1），平滑，更新效率高
  • 缺点
    梯度消失

线性（ReLU）修正函数

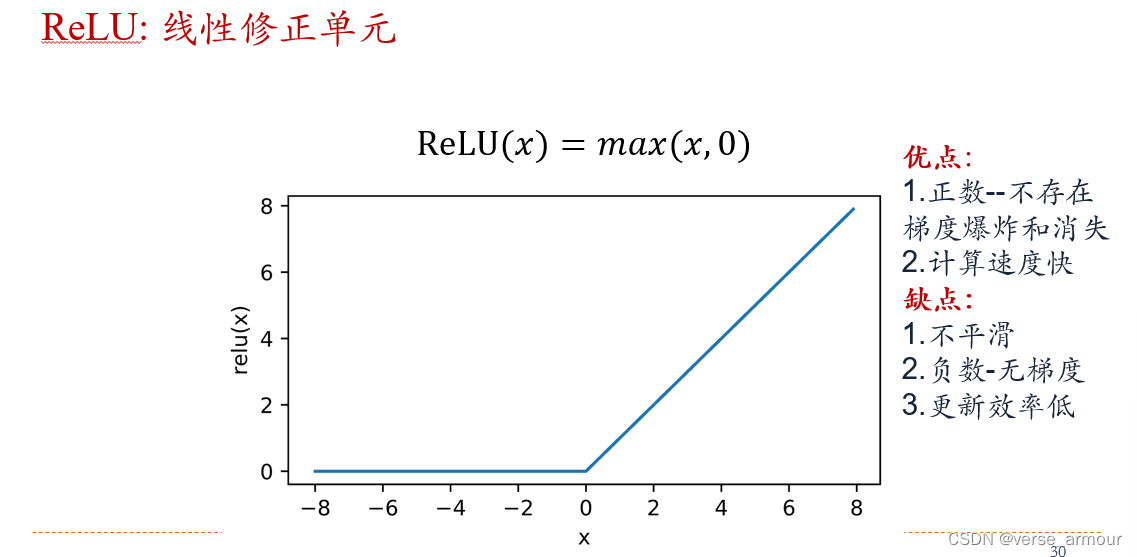
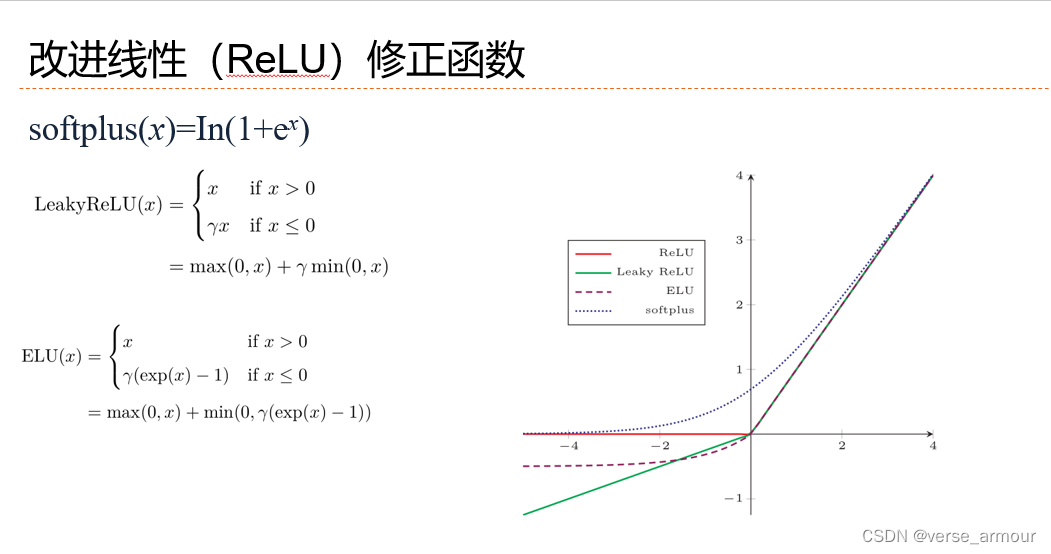
在这里插入图片描述
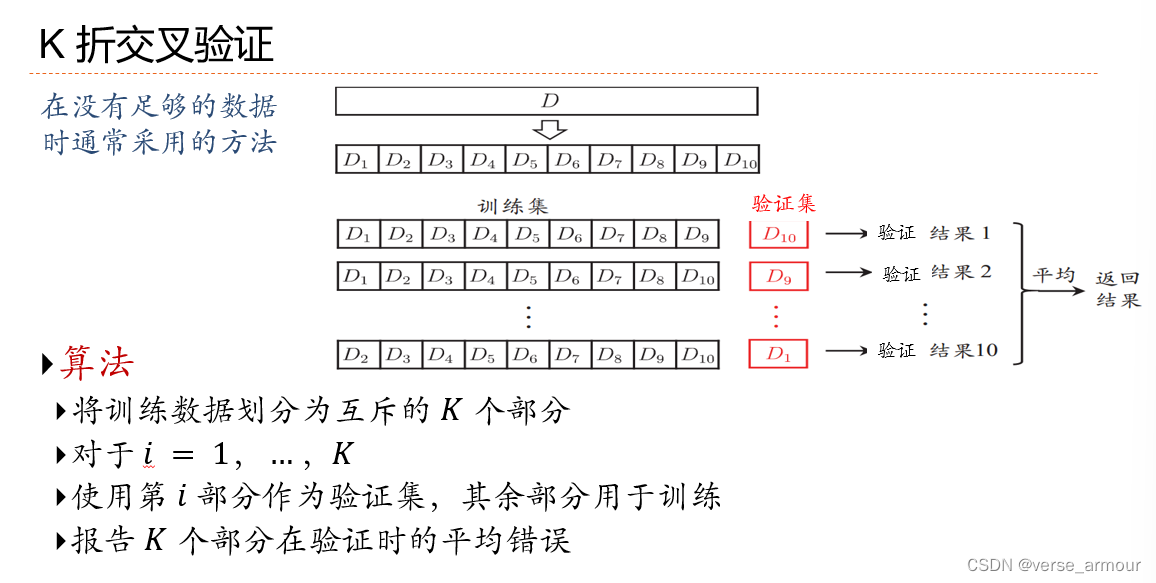
在这里插入图片描述

MLP

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

K折交叉验证

在这里插入图片描述
在这里插入图片描述

估计模型的复杂度

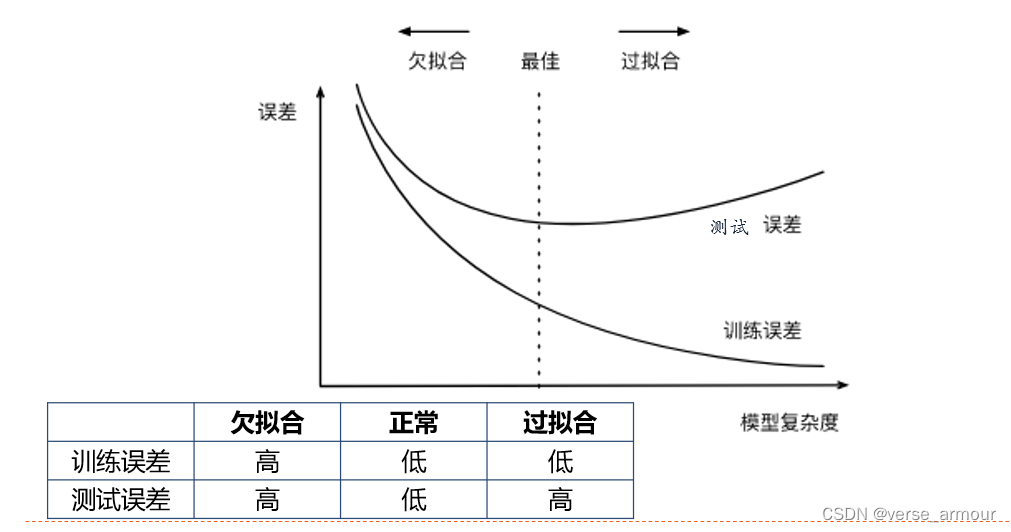
在这里插入图片描述

数据复杂度

在这里插入图片描述

欠拟合和过拟合

在这里插入图片描述

欠拟合和过拟合的原因

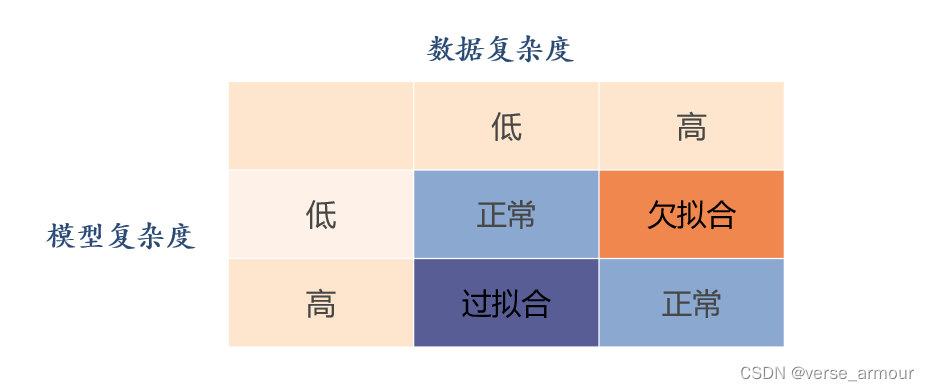
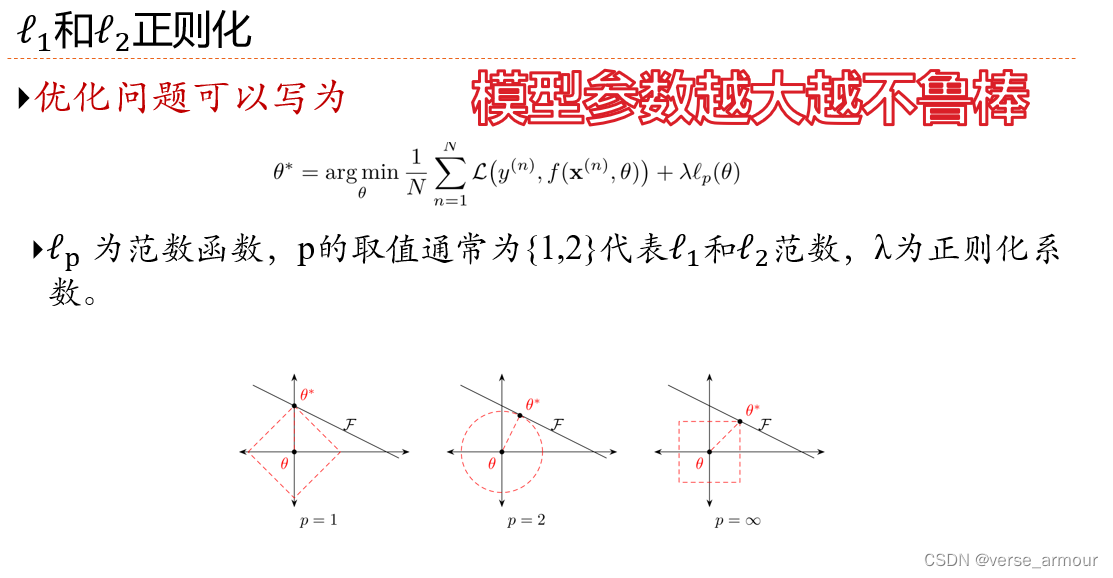
在这里插入图片描述

正则化

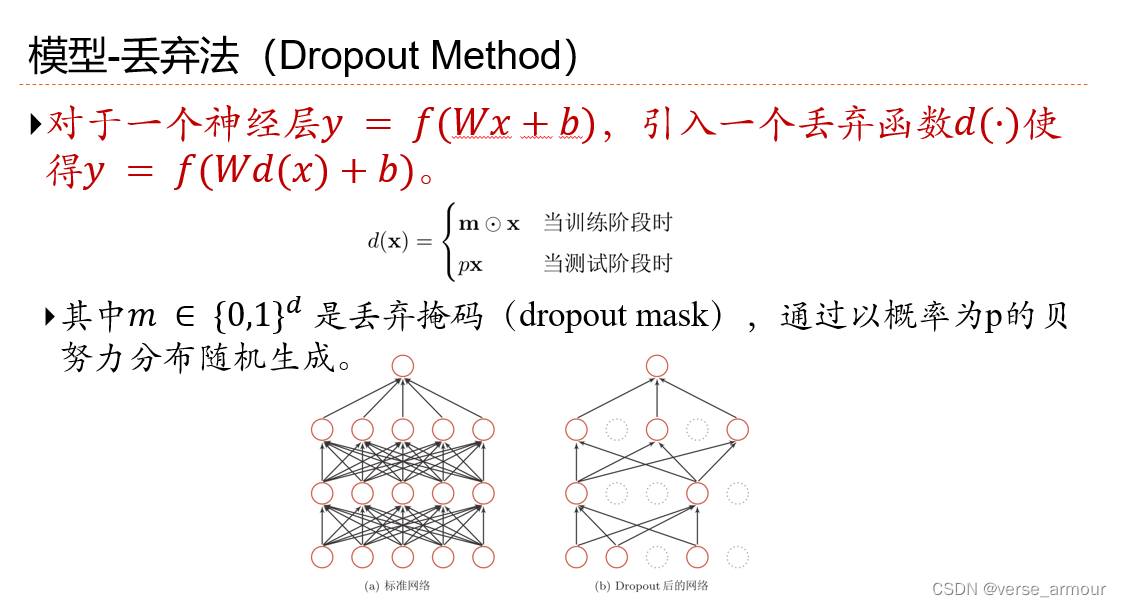
在这里插入图片描述

Dropout

在这里插入图片描述

梯度爆炸和梯度消失

在这里插入图片描述

在这里插入图片描述

权重初始化

在这里插入图片描述

参数初始化

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/173208.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Unity的碰撞检测(六)

Unity的碰撞检测(六)

温馨提示：本文基于前一篇“Unity的碰撞检测(五)”继续探讨两个游戏对象具备刚体的BodyType均为Dynamic，但是Collision Detection属性不同的碰撞检测，阅读本文则默认已阅读前文。 （一）测试说明 在基于两个游戏对象都具…
阅读更多...
网络原理之TCP/IP

网络原理之TCP/IP

文章目录 应用层传输层UDP协议TCP协议TCP 的工作机制1. 确认应答2. 超时重传3. 连接管理TCP 的建立连接的过程(三次握手),和断开连接的过程(四次挥手)TCP 断开连接, 四次挥手 3. 滑动窗口5. 流量控制6. 拥塞控制7. 延时应答8. 捎带应答9. 面向字节流10. 异常情况 本章节主要讨论…
阅读更多...
帆软report JS实现填报控件只能填写一次

帆软report JS实现填报控件只能填写一次

效果 方法： 代码： if(this.getValue()!"")//判断这个控件框是否有值，这里是不为空{this.setEnable(false)}//不为空，则不能再修改else{this.setEnable(true)}//为空，可以编辑
阅读更多...
音画欣赏|《诗和远方》

音画欣赏|《诗和远方》

《诗和远方》 8050cm 陈可之2020年绘 面朝大海，春暖花开 [海子] 从明天起，做一个幸福的人 喂马、劈柴，周游世界 从明天起，关心粮食和蔬菜 我有一所房子，面朝大海，春暖花开 从明天起，和每一…
阅读更多...
图神经网络论文笔记（一）——北邮：基于学习解纠缠因果子结构的图神经网络去偏

图神经网络论文笔记（一）——北邮：基于学习解纠缠因果子结构的图神经网络去偏

作者 ：范少华 研究方向 ：图神经网络 论文标题 ：基于学习解纠缠因果子结构的图神经网络去偏 论文链接 ：https://arxiv.org/pdf/2209.14107.pdf        https://doi.org/10.48550/arXiv.2209.14107 大多数图神经网络(GNNs)通…
阅读更多...
通道洗牌的思想神了

通道洗牌的思想神了

大家好啊，我是董董灿。 昨天写了一篇关于分组卷积的文章：分组卷积的思想神了，然后有同学希望多了解下通道洗牌。 我个人感觉，通道洗牌这个算法，或者说这个思想，可以称之为小而精，并且是实际解…
阅读更多...
Chatgpt网页版根据关键词自动批量写原创文章软件【可多开自动登录切换gpt账号】

Chatgpt网页版根据关键词自动批量写原创文章软件【可多开自动登录切换gpt账号】

Chatgpt网页版根据关键词自动批量写原创文章软件介绍： 1、需要放入GPT账号和密码放入在账号库.txt里，可以放入多组账号密码，账号切换轮流使用。 2、可以自定义回答指令，也可多个回答指令随机切换。 3、可以给关键词加双标题&…
阅读更多...
听GPT 讲Rust源代码--library/std(6)

听GPT 讲Rust源代码--library/std(6)

题图来自 Why you should use Python and Rust together[1] File: rust/library/std/src/sys/unix/thread_parking/netbsd.rs 文件netbsd.rs位于Rust源代码的rust/library/std/src/sys/unix/thread_parking目录下。该文件是Rust标准库中用于Unix操作系统的线程等待和唤醒机制的…
阅读更多...
CAN接口的PCB Layout规则要求汇总

CAN接口的PCB Layout规则要求汇总

随着时代高速发展，控制器局域网（CAN）接口的应用越来越广泛，尤其是在汽车电子、航空航天等领域中发挥着重要作用，为了确保CAN接口的可靠性和稳定性，工程师必须在其PCB Layout方面下功夫，下面来看…
阅读更多...
git clone 遇到了 early EOF index-pack failed 问题

git clone 遇到了 early EOF index-pack failed 问题

问题 由于仓库包含了很多文件，仓库过大，导致clone的时候一直报错： 解决方案 注意：过程中需要耐心等待，如果遇到失败，可以多尝试几遍。 压缩目标仓库文件 compression 是压缩的意思，从 clo…
阅读更多...
拉扎维模拟CMOS集成电路设计西交张鸿老师课程P10~13视频学习记录

拉扎维模拟CMOS集成电路设计西交张鸿老师课程P10~13视频学习记录

--------------------------------------------------------------------------------------------------------------------------------- p10 短沟道，除了沟长调，还可能出现速度饱和问题； 但是在拉扎维这本书里面没有考虑这个问题&#…
阅读更多...
python安装库

python安装库

查看安装的库 按下开始r 输入cmd 查看python版本 查看python所有库 安装一个库 在pycharm里面查看库文件 在pycharm里面安装库 在anaconda里面安装库和查看库
阅读更多...
SpreadJS 16.2.2 + GcExcel 6.2.3 相结合，还有更强的吗

SpreadJS 16.2.2 + GcExcel 6.2.3 相结合，还有更强的吗

SpreadJS GcExcel 相结合，还有更强的吗？ 内容摘自互联网，，， 设计思路篇 Excel是我们日常办公中最常用的电子表格程序，不仅可满足报表数据的计算需求，还可提供绘图、数据透视分析、BI和Visual…
阅读更多...
GPT的广泛应用会对互联网公司造成挑战吗？——探讨GPT在实际使用中的应用和影响

GPT的广泛应用会对互联网公司造成挑战吗？——探讨GPT在实际使用中的应用和影响

文章目录 前言GPT 技术的背景和发展历程GPT 技术对互联网行业的影响GPT 技术在互联网行业中的应用GPT 技术对于用户隐私和数据安全的威胁GPT 技术对于人类工作岗位的影响加强 AI 伦理和监管加强 AI 安全性和隐私保护推动 AI 创新和发展，避免过度依赖 AIGPT 技术是一…
阅读更多...
C++设计模式_15_Proxy 代理模式

C++设计模式_15_Proxy 代理模式

Proxy 代理模式也是属于“接口隔离”模式，通过增加一层间接层来解决问题的模式。 文章目录 1. 动机( Motivation)2. 模式定义3. 结构( Structure )4. 代码演示Proxy 代理模式4.1 常规方法4.2 Proxy 代理模式 5. 要点总结6. 其他参考 1. 动机( Motivation) 在面向对…
阅读更多...
基于AI与物联网技术的智能视频监控系统架构剖析

基于AI与物联网技术的智能视频监控系统架构剖析

智能视频监控系统正逐渐成为我们日常生活和工作中不可或缺的一部分。基于物联网的智能监控系统架构为我们在各个领域提供了更高效、智能化和安全的监控解决方案。本文将以旭帆科技EasyCVR视频监控云平台为例，介绍基于AI、物联网的智能监控系统的架构，并探…
阅读更多...
【Linux】：进程程序替换

【Linux】：进程程序替换

进程程序替换 一.替换原理二.替换函数三.exec类函数 一.替换原理 用fork创建子进程后执行的是和父进程相同的程序(但有可能执行不同的代码分支)，子进程往往要调用一种exec函数以执行另一个程序。当进程调用一种exec函数时，该进程的用户空间代码和数据完全…
阅读更多...
STM32 TIM（四）编码器接口

STM32 TIM（四）编码器接口

STM32 TIM（四）编码器接口 编码器接口简介 Encoder Interface 编码器接口 编码器接口可接收增量（正交）编码器的信号，根据编码器旋转产生的正交信号脉冲，自动控制CNT自增或自减，从而指示编码器的…
阅读更多...
Java中级面试题记录(四)

Java中级面试题记录(四)

一面面试题 1.Innodb的行数据存储模式 https://baijiahao.baidu.com/s?id1775090633458928876&wfrspider&forpc 2.行数据包含哪些信息？ https://baijiahao.baidu.com/s?id1775090633458928876&wfrspider&forpc 3.MySQL在进行存储VARCHAR的时…
阅读更多...
python：使用Scikit-image对遥感影像进行尺度空间特征提取（scale-space）

python：使用Scikit-image对遥感影像进行尺度空间特征提取（scale-space）

作者：CSDN @ _养乐多_ 在本博客中，我们将介绍如何使用Scikit-Image来进行尺度空间特征提取，并且提供一个示例代码，演示了如何在单波段遥感图像上应用这些方法。 尺度空间特征提取是一种处理图像的方法，旨在检测不同尺度下的特征和结构。这对于处理遥感图像非常有用，因为…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023