上一篇:2 用TensorFlow构建一个简单的神经网络-CSDN博客
1、神经网络概念
接上一篇,用tensorflow写了一个猜测西瓜价格的简单模型,理解代码前先了解下什么是神经网络。
下面是百度AI对神经网络的解释:

这里不赘述太多概念相关的东西,不理解可先跳过,后面例子看懂了在返回看可能就理解了。
2、密集层
再看看上一篇预测西瓜价格的代码
import numpy as np
import tensorflow as tf# 西瓜的重量
weight = np.array([1, 3, 4, 5, 6, 8], dtype=float)# 对应的费用
total_cost = np.array([1.7, 4.1, 5.3, 6.5, 7.7, 10.1], dtype=float)model = tf.keras.Sequential([tf.keras.layers.Dense(1, input_shape=[1])
])model.compile(loss=tf.losses.mean_squared_error, optimizer='SGD')history = model.fit(weight, total_cost, epochs=500)# 训练完成后,预测10斤西瓜的总费用
print(model.predict([10]))其中这行代码:
model = tf.keras.Sequential([
tf.keras.layers.Dense(1, input_shape=[1])
])
意思是构建了一个模型,里面添加了一层神经网络,只有一个神经元。(Sequential是顺序的意思,Dense是密集层。)
密集层(也叫全连接层),在神经网络中指的是每个神经元都与前一层的所有神经元相连的层。
举个例子,如下图所示:神经元a1与所有输入层数据相连(X1,X2,X3),其他神经元也一样都与上一层神经元相连。
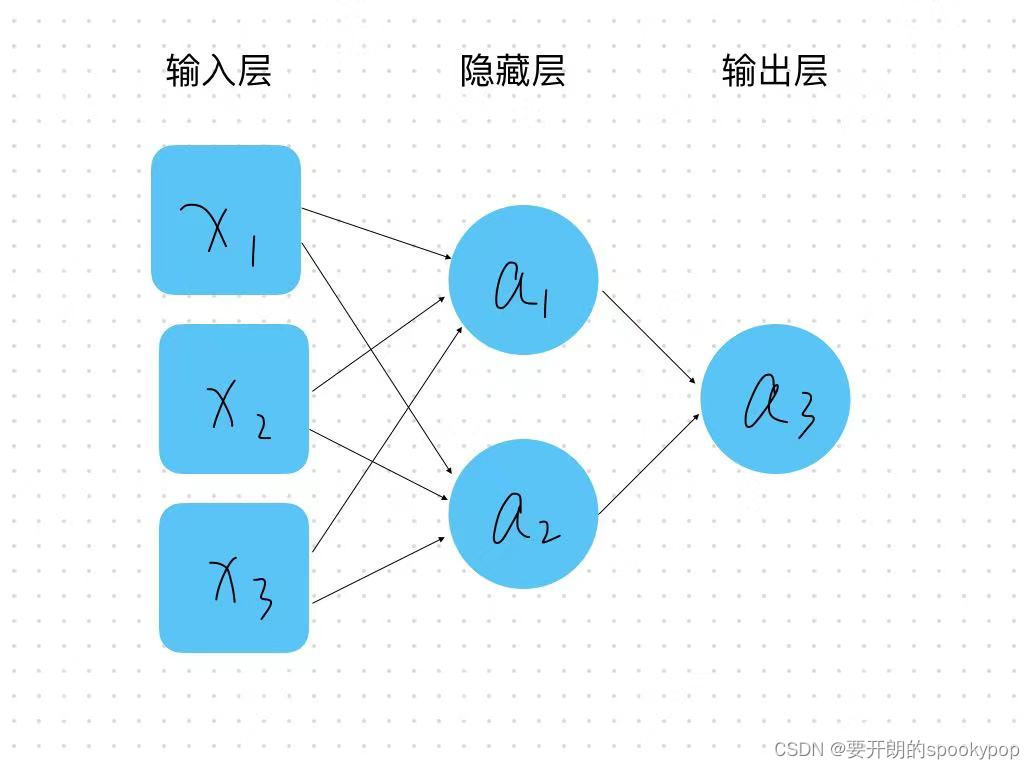
它们之间的数学关系为:
某个神经元是由连接的上一层神经元分别乘上权重(w),再加上偏差(b)得到,例如计算a1:
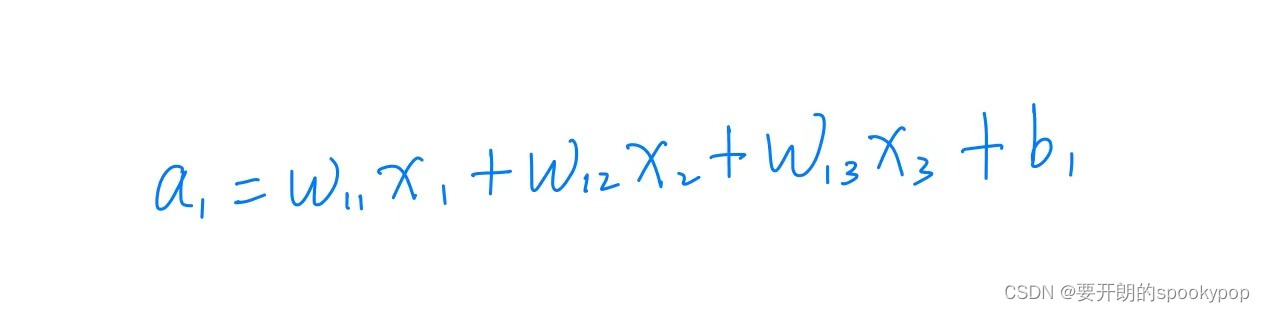
权重w的数字下标可以按照顺序命名,比如第一个神经元计算的权重可以为w11、w12……,第二个神经元计算的权重可以为w21、w22……
a2、a3计算以此类推。
3、西瓜预测模型详解
上一篇西瓜费用计算公式 :费用=1.2元/斤*重量+0.5元
即:y=1.2x+0.5
这是一个一元线性回归问题,只有一个自变量x和一个因变量y,机器学习要推算出权重w=1.2, 偏差b=0.5,才能准确预测费用。
下面是实现这个算法的流程:
(1)训练数据准备
西瓜重量 weight=[1, 3, 4, 5, 6, 8]
对应的费用 total_cost=[1.7, 4.1, 5.3, 6.5, 7.7, 10.1]
(2)构建模型
model = tf.keras.Sequential([
tf.keras.layers.Dense(1, input_shape=[1])
])
- tf.keras.layers.Dense(1, input_shape=[1]),参数1表示1个神经元,我们只要预测费用y,所以输出层只要一个神经元就可以了(注意:神经元不用包含输入层)。
- input_shape=[1],表示输入数据的形状为单元素列表,即每个输入数据只有一个值。因为只有一个变量x(西瓜的重量),所以此处输入形状是[1]
该模型的示意图:

可以用model.summary()查看模型摘要,代码如下:
import numpy as np
import tensorflow as tf# 西瓜的重量
weight = np.array([1, 3, 4, 5, 6, 8], dtype=float)# 对应的费用
total_cost = np.array([1.7, 4.1, 5.3, 6.5, 7.7, 10.1], dtype=float)model = tf.keras.Sequential([tf.keras.layers.Dense(1, input_shape=[1])
])# 查看模型摘要
model.summary()运行结果:

可以看到可训练参数有2个,即公式中的w1和b1。
(3)设置损失函数和优化器
model.compile(loss=tf.losses.mean_squared_error, optimizer='SGD')
- mean_squared_error是均方误差,指的是预测值与真实值差值的平方然后求和再平均。公式为:
MSE=1/n Σ(P-G)^2 (P为预测值,G为真实值)
- SGD即随机梯度下降(Stochastic Gradient Descent),是一种迭代优化算法。
(4)设置训练数据
history = model.fit(weight, total_cost, epochs=500)
- 设置训练数据的特征和标签,在上述代码中分别是西瓜的重量和费用:weight、total_cost
- 设置训练轮次epochs=500,1个epochs是指使用所有样本训练一次。
(5) 查看训练结果
看下面的训练过程,第8个epoch的时候损失值loss已经很小了,训练轮次不需要设置到500就可以有很好的预测效果了。
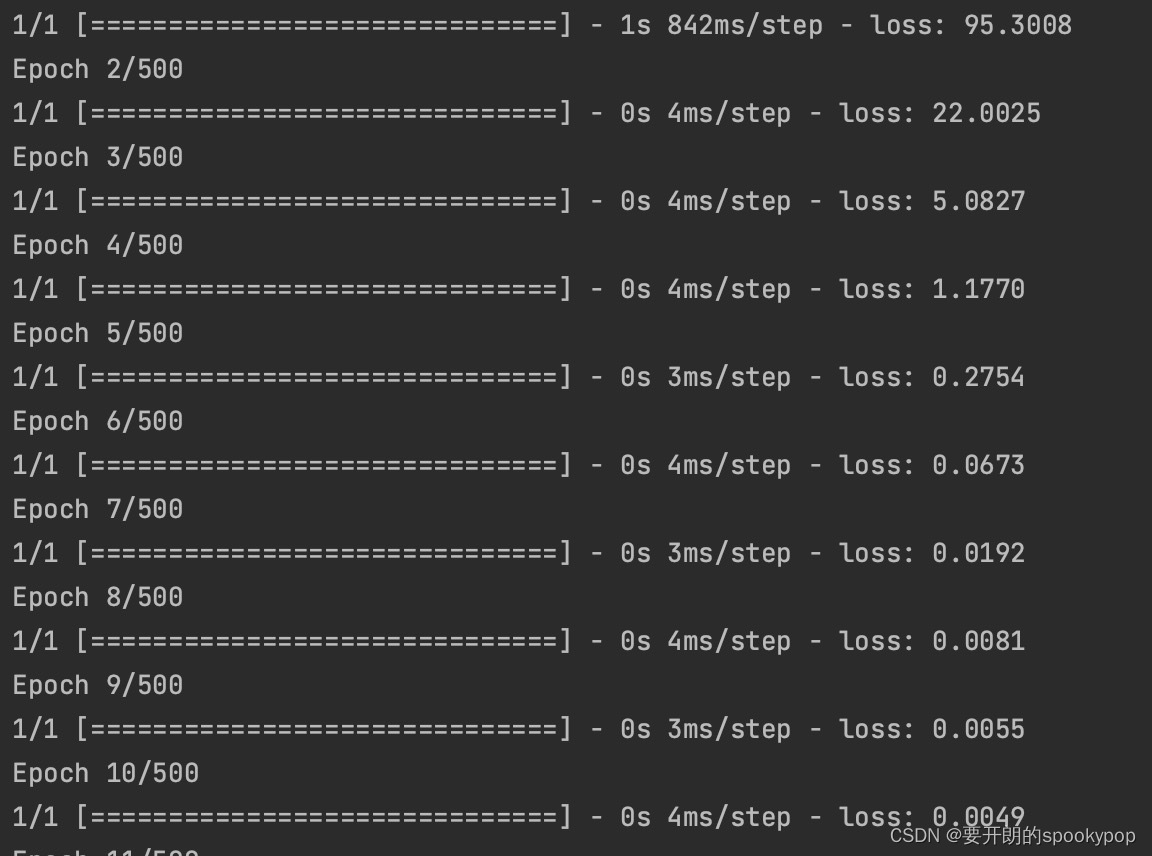
刚开始loss很高,使用优化算法慢慢调整了权重,loss值可以很好地衡量我们的模型有多好。
我们把epoch的值调小,看看程序猜测的权重(w)和偏差(b)是多少,以及loss值的计算。
代码改动如下:
- epochs=5
- 用model.get_weights()获取程序猜测的权重数据
import numpy as np
import tensorflow as tf# 西瓜的重量
weight = np.array([1, 3, 4, 5, 6, 8], dtype=float)# 对应的费用
total_cost = np.array([1.7, 4.1, 5.3, 6.5, 7.7, 10.1], dtype=float)model = tf.keras.Sequential([tf.keras.layers.Dense(1, input_shape=[1])
])model.compile(loss=tf.losses.mean_squared_error, optimizer='SGD')history = model.fit(weight, total_cost, epochs=5)# 获取权重数据
w = model.get_weights()[0]
b = model.get_weights()[1]print('w:')
print(w)
print('b: ')
print(b)# 训练完成后,预测10斤西瓜的总费用
print(model.predict([10]))运行结果:
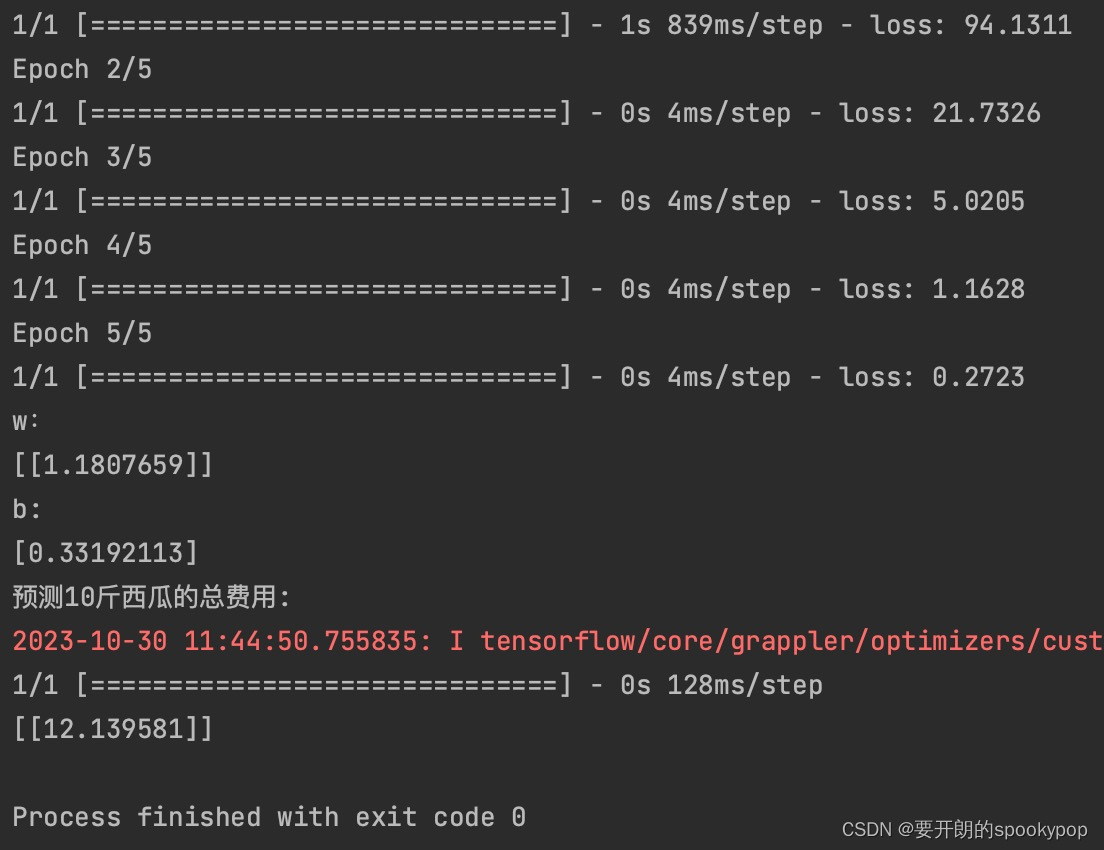
训练了5个epoch后,程序猜测w是1.1807659,b为0.33192113
y=wx+b=1.1807659*10+0.33192113=12.139581
所以预测10斤西瓜的总费用是12.139581