题目1：
这篇帖子中有多道题，由浅入深。
arr是货币数组，其中的值都是正数。再给定一个正数aim。每个值都认为是一张货币，即便是值相同的货币也认为每一张都是不同的，返回组成aim的方法数。
例如：arr = {1,1,1}，aim = 2
第0个和第1个能组成2，第1个和第2个能组成2，第0个和第2个能组成2
一共就3种方法，所以返回3

暴力递归
这道题相对来讲比较基础，很简单的从左往右尝试模型，给定的arr数组中，从左向右依次尝试，每个arr[index]一共就2种情况：要 和 不要。
并且确定好base case（何时终止递归）：
第一种情况就是当index = arr.length时， 我的数组已经到尾了，取不出来东西了。
第二种是如果使用了当前arr[index]处的值，则用aim - arr[index]后，用rest（剩余钱数）向下传递，如果rest 为 0时，说明正好凑够了这个钱，也return。

代码

 public static int coinWays(int[] arr, int aim) {return process(arr, 0, aim);}public static int process(int[] arr, int index, int rest) {if (rest < 0) {return 0;}if (index == arr.length) {return rest == 0 ? 1 : 0;} else {// process(arr, index + 1, rest) 不要当前的钱// process(arr, index + 1, rest - arr[index]) 要当前的钱，则剩余钱数rest要 减去 arr[index]return process(arr, index + 1, rest) + process(arr, index + 1, rest - arr[index]);}}

动态规划
根据上面暴力递归代码改写动态规划，可变参数是index（数组下标）和 rest（剩余钱数），并且index可以到达arr.length的位置，rest也可能会为0，所以可以确定 dp[][] 大小为 dp[arr.length + 1][aim + 1]。
根据base case 可以确定 dp[arr.length][0]位置的值是1，其余的按照顺序遍历填充即可。

代码

    public static int dp(int[] arr, int aim) {if (aim == 0) {return 1;}int N = arr.length;int[][] dp = new int[N + 1][aim + 1];dp[N][0] = 1;for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= aim; rest++) {dp[index][rest] = dp[index + 1][rest] + (rest - arr[index] >= 0 ? dp[index + 1][rest - arr[index] ]: 0);}}return dp[0][aim];}

题目2
arr是面值数组，其中的值都是正数且没有重复。再给定一个正数aim。每个值都认为是一种面值，且认为张数是无限的。返回组成aim的方法数
例如：arr = {1,2}，aim = 4
方法如下：1+1+1+1、1+1+2、2+2
一共就3种方法，所以返回3

暴力递归
整体思路依然是先从暴力递归代码开始写起，并根据暴力递归代码改写动态规划。
暴力递归方法的整体思路是这样：
依然是数组从左向右的不停尝试，因为数组中每个数值张数都可以当做是无限的，所以利用循环来看当前数值的数使用0张情况，使用1张情况，使用2张情况。。。 将结果值进行累加，即为总方法数。
所以暴力递归方法需要的参数：1. arr数组 2.rest 剩余钱数 3. index 数组下标
确定了暴力递归的尝试方法后，base case也就自然而然的出来了，那就是当 index = arr.length时，数组中没有钱可以取了，此时如果剩余钱数 rest = 0，说明利用数组中数值正好拼凑出来了正好的钱数，return 1。 否则 return 0。

代码

public static int coinsWay(int[] arr, int aim) {if (arr == null || arr.length == 0) {return -1;}return process(arr, aim, 0);}public static int process(int[] arr, int rest, int index) {if (index == arr.length) {return rest == 0 ? 1 : 0;}int ways = 0;//循环：当前数值从0张开始，不停尝试， 条件是 当前面值的钱使用几张，都不可以超过剩余钱数 rest。for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {ways += process(arr, rest - zhang * arr[index], index + 1);}return ways;}

动态规划
根据暴力递归方法代码可以确定出可变参数为剩余钱数 rest 和 数组下标 index。
又因为代码中 index是可以到达数组arr的长度的，并且剩余钱数rest可以为 0 。所以dp[][] 的范围是 dp[arr.length + 1] [ rest + 1]。

第二步要根据base case来给dp表进行初始化赋值。代码中 当index = arr.length时，如果rest = 0 则return 1。其余情况 return 0。
int[] 创建后默认值就是 0 ，所以 dp[ arr.length ][ 0 ]位置的值 = 1。 其余照搬暴力递归代码即可。

代码

 public static int dp(int[] arr, int aim) {if (arr == null || arr.length == 0) {return -1;}int N = arr.length;int[][] dp = new int[N + 1][aim + 1];dp[N][0] = 1;for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= aim; rest++) {int ways = 0;for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {ways += dp[index + 1][rest - zhang * arr[index]];}dp[index][rest] = ways;}}return dp[0][aim];}

优化

关于上面的代码。逻辑上已经跑通了，但是关于dp表的整体构建生成还是过于复杂，因为zhang的for中枚举了数组中的每个数值的从 0 ~ zhang * arr[index] <= rest的所有情况。
如果有从暴力递归转动态规划（一）看到现在的会有发现，早期文章中整体的解题过程是 暴力递归 -》 傻缓存（记忆化搜索 - 看dp表中是否有当前值，没有则进行计算） -》 严格表结构依赖（根据每个格子的依赖关系，从底层向上构建dp表）。
没有枚举过程时，傻缓存和严格表结构依赖的时间复杂度相同。
但是这道题不太一样，因为之前的题目中，构建dp表中每个位置都是一个常数时间操作，而这道题里。构建dp表的每个格子都要进行for循环，这种情况下，如果不进行优化，那么时间复杂度大大增加（时间复杂度看枚举过程中的分支数量）。

思路
这种优化最简单直观的方法就是进行画图。将暴力递归方法中代码，根据依赖关系，直观的展现在图示中。

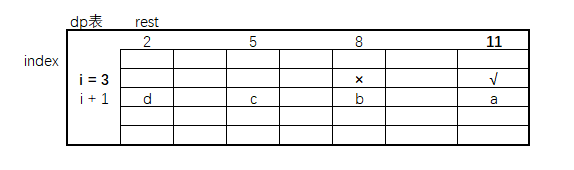
拿这张图举例，当rest = 11时（√位置），来看下它的依赖关系，根据暴力递归代码 index + 1 ，rest - zhang * arr[index]，最开始使用的是0张，所以是rest - 0，那么在表中的依赖关系就是a位置，接下来是来使用1张、使用2张、使用3张。分别依赖的是bcd的位置。
那当rest = 8 时呢？此时使用1张2张3张，依赖的就是bcd位置。那 √ 位置的结果，之前是a+b+c+d，找到依赖关系后就可以发现，此时用 x + a = √。依赖关系已找到，可以根据这种严格的表结构依赖来进行优化。

代码

public static int bestDP(int[] arr, int aim) {if (arr == null || arr.length == 0) {return -1;}int N = arr.length;int[][] dp = new int[N + 1][aim + 1];dp[N][0] = 1;for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= aim; rest++) {dp[index][rest] = dp[index + 1][rest];//如果左边不越界if (rest - arr[index] >= 0) {dp[index][rest] += dp[index][rest - arr[index]];}}}return dp[0][aim];}

题目3
arr是货币数组，其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币，认为值相同的货币没有任何不同，返回组成aim的方法数
例如：arr = {1,2,1,1,2,1,2}，aim = 4 方法：1+1+1+1、1+1+2、2+2
一共就3种方法，所以返回3。

暴力递归
这个题目和第二题类似，区别在于第二题中每种面值是无限张的，不过这里是有限张数。所以这道题的整体解题思路也和第二题类似。

1. 先将给定数组进行封装，封装的类中有 int[] coins类型 代表每种不同的面值，以及 int[] zhangs 代表着每种面值对应的张数。
2. 暴力递归过程也和第二题类似，不过需要判断，for循环中每种面值使用的张数不能大于 zhangs[index] 中的值，以及 zhang * coins[index] 也要不能大于rest。

代码

//将给定的arr封装成Info对象
static class Info {int[] coins;int[] zhangs;public Info(int[] coins, int[] zhangs) {this.coins = coins;this.zhangs = zhangs;}public int[] getCoins() {return coins;}public int[] getZhangs() {return zhangs;}}// arr转换成Info的方法类public static Info getInfo(int[] arr) {Map<Integer, Integer> infoMap = new HashMap<>();for (int num : arr) {if (!infoMap.containsKey(num)) {infoMap.put(num, 1);} else {infoMap.put(num, (infoMap.get(num) + 1));}}int N = infoMap.size();int[] coins = new int[N];int[] zhangs = new int[N];int index = 0;for (Map.Entry<Integer, Integer> entries : infoMap.entrySet()) {coins[index] = entries.getKey();zhangs[index++] = entries.getValue();}return new Info(coins, zhangs);}//暴力递归主方法public static int coinsWay(int[] arr, int aim) {if (arr == null || arr.length == 0) {return -1;}Info info = getInfo(arr);return process(info.getCoins(), info.getZhangs(), aim, 0);}public static int process(int[] coins, int[] zhangs, int rest, int index) {if (index == zhangs.length) {return rest == 0 ? 1 : 0;}int ways = 0;// 判断的逻辑： //zhang 要 <= 每种面值给定的张数//rest - 面值 * 使用的张数 >= 0			for (int zhang = 0; zhang <= zhangs[index] && zhang * coins[index] <= rest; zhang++) {ways += process(coins, zhangs, rest - zhang * coins[index], index + 1);}return ways;}

动态规划
动态规划思路也和第二题大致相同，根据可变参数index和rest确定dp表范围，而后循环遍历填充dp表。

代码

 public static int dp(int[] arr, int aim) {if (arr == null || arr.length == 0) {return -1;}Info info = getInfo(arr);int[] zhangs = info.getZhangs();int[] coins = info.getCoins();int N = zhangs.length;int[][] dp = new int[N + 1][aim + 1];dp[N][0] = 1;for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= aim; rest++) {int ways = 0;for (int zhang = 0; zhang <= zhangs[index] && zhang * coins[index] <= rest; zhang++) {ways += dp[index + 1][rest - zhang * coins[index]];}dp[index][rest] = ways;}}return dp[0][aim];}

优化
动态规划中又见到了填充dp表时的枚举过程，所以可以根据严格的表结构依赖，根据画图，找到每个格子在dp表中的依赖关系，从而替代代码中的枚举for循环。
需要注意的是：这次的优化和第二题不同的在于，每种张数是固定的，而第二题每种张数是无限张的。
所以，要考虑到张数的限制，还是回归到图示当中去。
数组中面值有 1,3,5 每种面值各2张，依然是rest = 11，面值 = 3时为例。

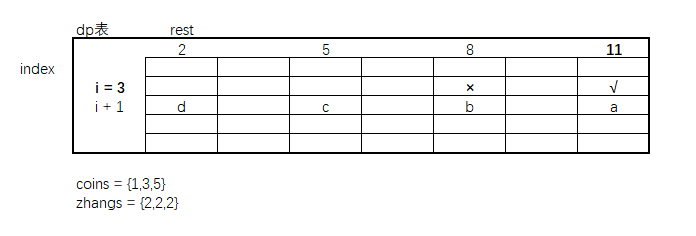
当rest = 11时，面值为3的情况一共有abc三种，对应着3面值的数使用了0、1、2张的情况。
再来看X的位置，此时情况为bcd，第二题要想求√位置，需要 x + a，因为是无限张，但是本题中。如果依然是X + a，那么会多加一个d，张数的使用会多一张。所以在求√时，需要将d位置减掉。
接下来我们将它抽象化一下，根据暴力递归的代码带入公式。
假设此时是m面值，共有n张 , √此时在 i 行，剩余钱数rest，。
那此时a位置就是：dp[index + 1][rest]
此时的x位置就是： dp[index][rest - 一张面值]
d的位置就是： dp[index + 1][ rest - 一张面值 * (面值张数 + 1)]

代码

public static int beatDP(int[] arr, int aim) {Info info = getInfo(arr);int[] zhangs = info.getZhangs();int[] coins = info.getCoins();int N = zhangs.length;int[][] dp = new int[N + 1][aim + 1];dp[N][0] = 1;for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= aim; rest++) {//先取得下面的dp[index][rest] = dp[index + 1][rest];//如果左侧也有，那么就 累加if (rest - coins[index] >= 0) {dp[index][rest] += dp[index][rest - coins[index]];}//如果左侧不越界，则减去多余的那一个if (rest - coins[index] * (zhangs[index] + 1) >= 0) {dp[index][rest] -= dp[index + 1][rest - coins[index] * (zhangs[index] + 1)];}}}return dp[0][aim];}