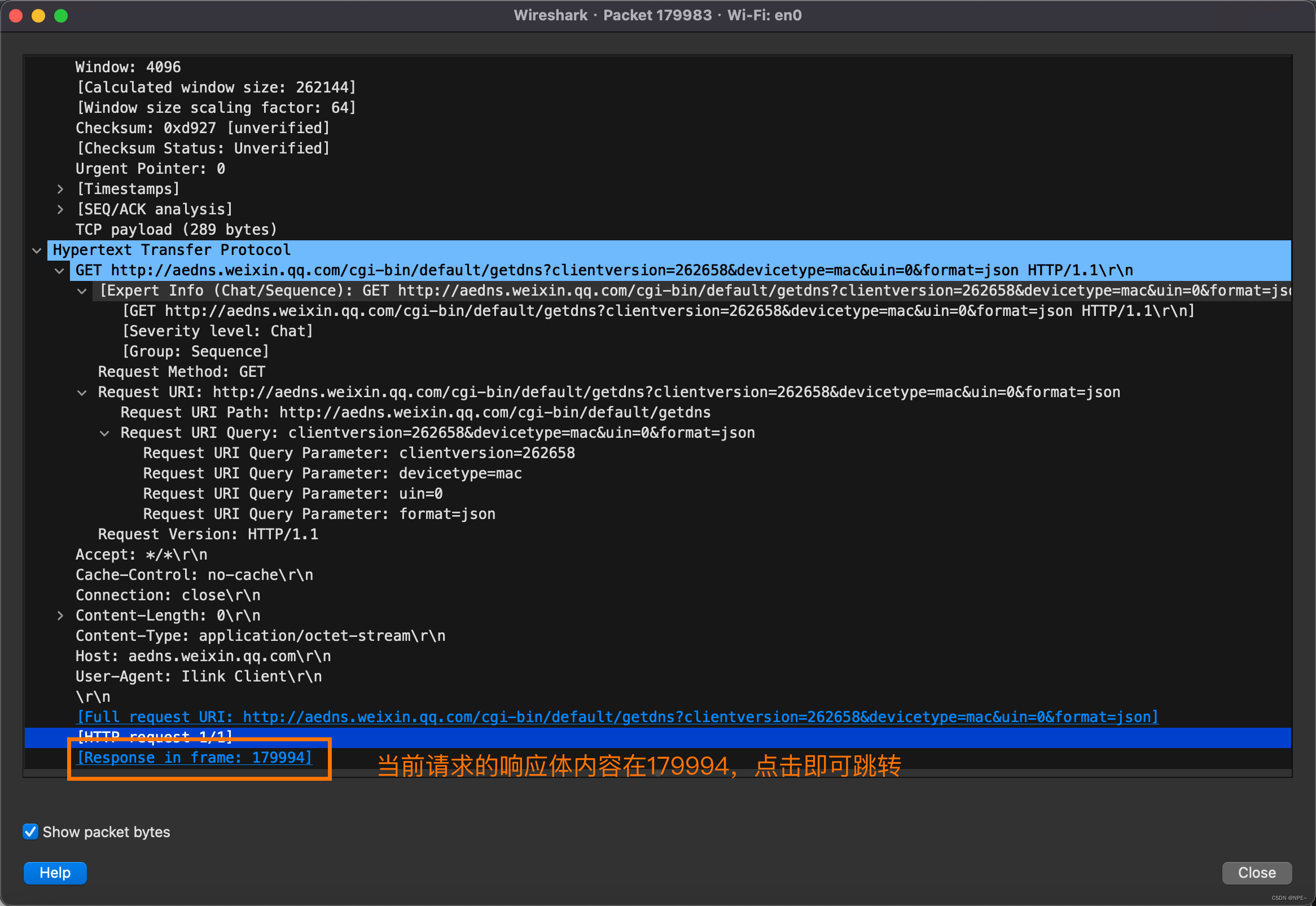
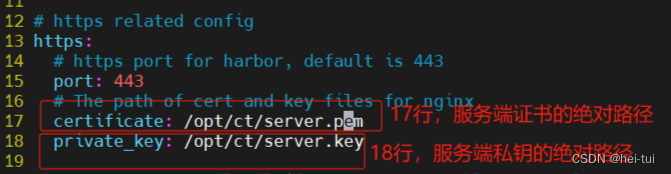
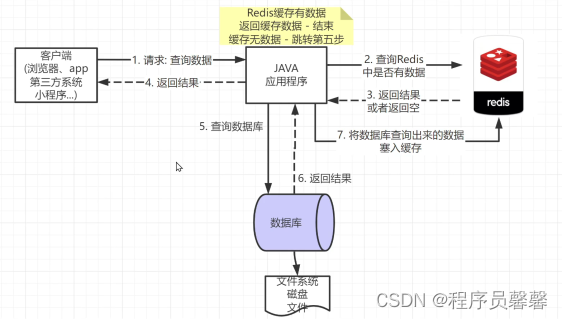
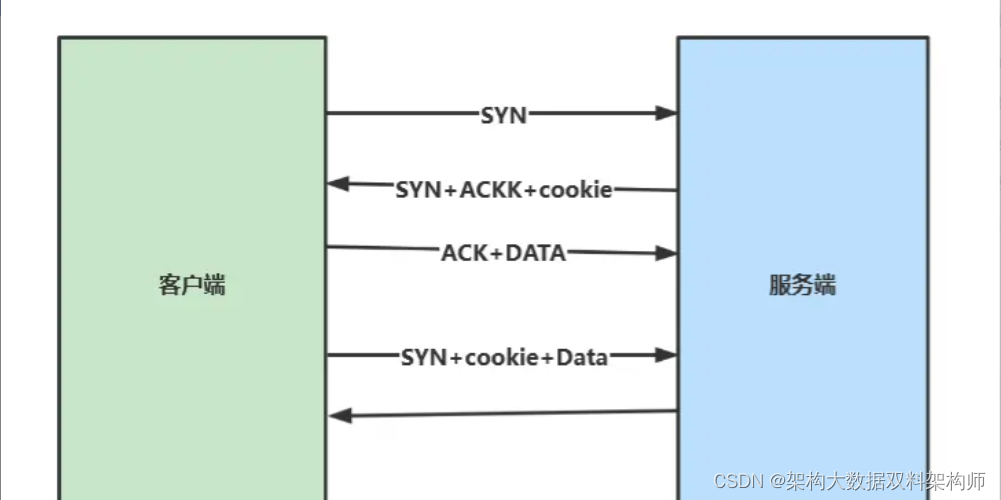
- B树和B+树的区别
- B树,也即balance树,是一棵多路自平衡的搜索树。它类似普通的平衡二叉树,不同的一点是B树允许每个节点有更多的子节点。
- B+树内节点不存储数据,所有关键字都存储在叶子节点上。
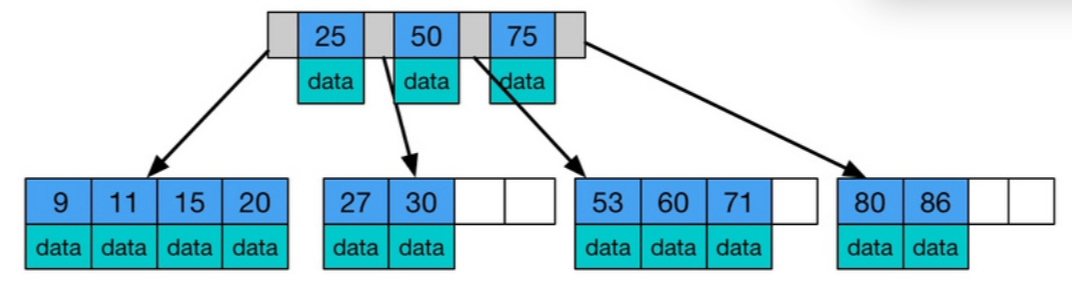
- B树:
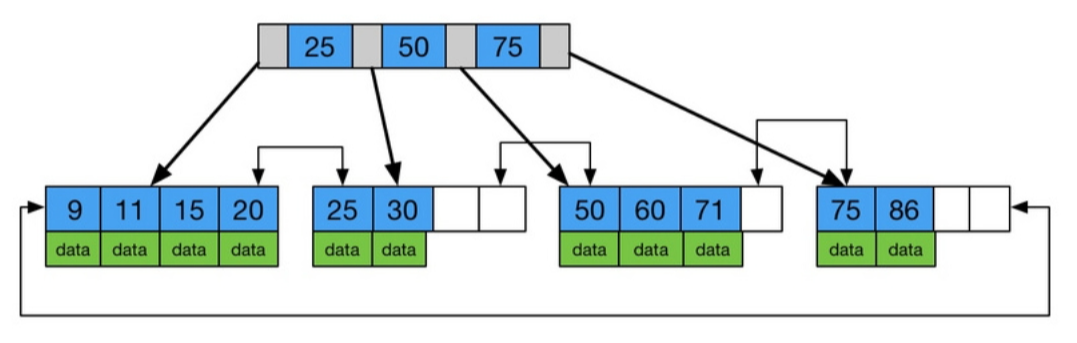
B+树:
二叉树理论基础:
1.种类:满二叉树、完全二叉树、二叉搜索树、平衡二叉树。
完全二叉树是最后一行从左到右连续但不一定全满。
二叉搜索树,必须有一定顺序。查询和添加都是O(logn),因为添加就是查询的过程。
平衡二叉搜索树:左右子树高度差的绝对值不超过1。map,set,multimap,multiset底层都是平衡二叉搜索树(是红黑树,红黑树是一种平衡二叉搜索树。)
2.存储方式:链表、数组。
链表,就是val,Treenode* left, Treenode *right
数组,一开始从0开始,左孩子就是2k+1,右孩子就是2k+2
3.遍历方式:
深度优先搜索:前序(中左右)、中序(左中右)、后序(左右中)。一般用递归实现,也可以迭代实现。
广度优先搜索:层序遍历是其中一种。
图的深度优先搜索就对应树的前中后序,图的广度优先搜索就对应树的层序遍历。
1. 二叉树的前,中,后序遍历 - 递归 leetcode144.94.145 20231026
代码随想录又卡了,栈与队列最后那题打着C++已实现的优先队列的旗号实际上是堆,而堆本身又是完全二叉树.....优先队列那题还不是直接拿的priority_queue去实现的,还自定义了它的比较规则,这又引出一个函数对象的概念,总之是无从下手,遂转战二叉树。今天看了看二叉树的理论知识,感觉还行,结果写题的时候又被递归摆了一道,完全忘了return和题干给的函数有什么用。
总之,题干给的preorderTraversal没动,自己重新实现了一个函数,调用之即可。下面两题是类似的。注意在preorder函数中,不能再写一个while循环了,这是写完迭代之后顺手写的错误。
class Solution { public:void preorder(TreeNode* cur, vector<int>& vct) {if(cur == nullptr){return;}vct.push_back(cur->val);preorder(cur->left,vct);preorder(cur->right,vct);}vector<int> preorderTraversal(TreeNode* root){vector<int> vct;preorder(root,vct);return vct;}};2. 二叉树的前,中,后序遍历 - 迭代leetcode144.94.145 20231027
迭代分为前后,中两种,理解起来其实还是很困难的,看代码貌似记住了,自己写对了,但是再过几天让我写是绝对写不出来的
前后之所以说是“一种”,因为后序可以由前序倒一下左右,再reverse一下数组就能得到。他们遍历和处理的顺序都是一样的,而中序就不一样了。
下面来看一下具体的代码~
前序,后序在这里就只放前序了:
class Solution { public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> stk;vector<int> vct;if(root == nullptr)return vct;stk.push(root);while(!stk.empty()){TreeNode* cur = stk.top();stk.pop();vct.push_back(cur->val);if(cur->right !=nullptr)stk.push(cur->right);if(cur->left !=nullptr)stk.push(cur->left);}return vct;} };定义一个stk用于模拟递归,一个vct用户返回数组。因为要先push root进去,所以先得判断一下是否为空。
root被push进去以后,只要栈不为空,就pop栈顶出来,再把刚出的栈顶push到 vct 里面去,然后先往栈里push右边,再往栈里push左边。这样的话,之后vct就会从栈顶开始出,就会先被push_back到vct里面去,而后又是往复的右左栈入,中(栈里元素)左右vct出。
注意,这里push左指针和右指针的时候我都进行了非空判断。后来我又写了一次,忘了加判断,直接往stk里push了空指针,但是用if(cur!=nullptr){}把vct的push_back和两个stk的push括起来了,照样通过,不加则不行。说明可以往栈里面push一个空指针,且stk.top()返回的就是这个空指针。中序
class Solution { public:vector<int> inorderTraversal(TreeNode* root) {vector<int> vct;stack<TreeNode*> stk;TreeNode* cur = root;while(cur != nullptr || !stk.empty()){if(cur != nullptr){stk.push(cur);cur = cur->left;//入栈,然后cur一直到最左边}else{cur = stk.top();//已经为空了,就取栈头的成为现在的curstk.pop();vct.push_back(cur->val);cur = cur->right;}}return vct;} };未完待续