2023-11-01 LeetCode每日一题（参加会议的最多员工数）

2023-11-01每日一题

一、题目编号

2127. 参加会议的最多员工数

二、题目链接

点击跳转到题目位置

三、题目描述

一个公司准备组织一场会议，邀请名单上有 n 位员工。公司准备了一张圆形的桌子，可以坐下 任意数目 的员工。

员工编号为 0 到 n - 1 。每位员工都有一位喜欢的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工不会是他自己。

给你一个下标从 0 开始的整数数组 favorite ，其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。

示例 1：
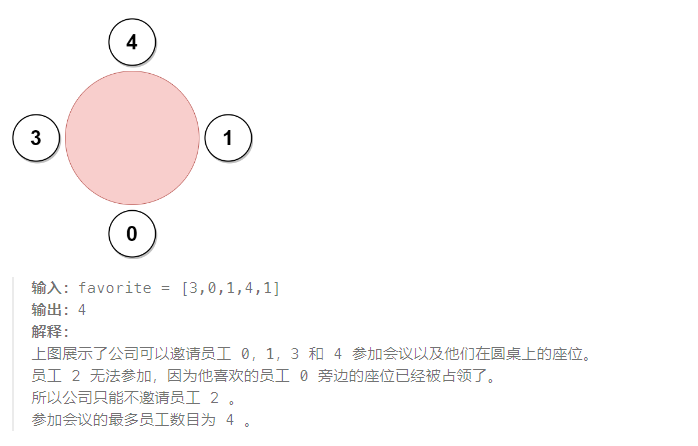
在这里插入图片描述

示例 2： 在这里插入图片描述

示例 3：
在这里插入图片描述

提示：

n == favorite.length
2 <= n <= 10⁵
0 <= favorite[i] <= n - 1
favorite[i] != i

四、解题代码

class Solution {
public:int maximumInvitations(vector<int>& favorite) {int n = favorite.size();// 统计入度，便于进行拓扑排序vector<int> indeg(n);for (int i = 0; i < n; ++i) {++indeg[favorite[i]];}vector<int> used(n), f(n, 1);queue<int> q;for (int i = 0; i < n; ++i) {if (!indeg[i]) {q.push(i);}}while (!q.empty()) {int u = q.front();used[u] = true;q.pop();int v = favorite[u];// 状态转移f[v] = max(f[v], f[u] + 1);--indeg[v];if (!indeg[v]) {q.push(v);}}// ring 表示最大的环的大小// total 表示所有环大小为 2 的「基环内向树」上的最长的「双向游走」路径之和int ring = 0, total = 0;for (int i = 0; i < n; ++i) {if (!used[i]) {int j = favorite[i];// favorite[favorite[i]] = i 说明环的大小为 2if (favorite[j] == i) {total += f[i] + f[j];used[i] = used[j] = true;}// 否则环的大小至少为 3，我们需要找出环else {int u = i, cnt = 0;while (true) {++cnt;u = favorite[u];used[u] = true;if (u == i) {break;}}ring = max(ring, cnt);}}}return max(ring, total);}
};