题目描述
这是 LeetCode 上的 「2127. 参加会议的最多员工数」 ,难度为 「困难」。
Tag : 「拓扑排序」、「内向基环树」、「图」
一个公司准备组织一场会议,邀请名单上有 n 位员工。
公司准备了一张圆形的桌子,可以坐下任意数目的员工。
员工编号为 到 。每位员工都有一位喜欢的员工,每位员工当且仅当他被安排在喜欢员工的旁边,他才会参加会议,每位员工喜欢的员工不会是他自己。
给你一个下标从 开始的整数数组 favorite,其中 表示第 位员工喜欢的员工。请你返回参加会议的最多员工数目。
示例 1: 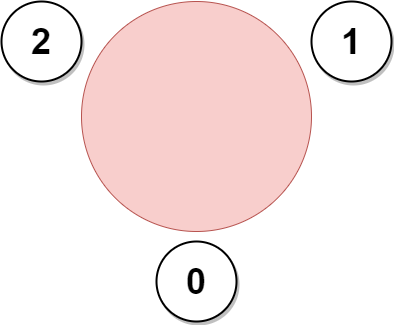
输入:favorite = [2,2,1,2]
输出:3
解释:
上图展示了公司邀请员工 0,1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议,因为员工 2 没办法同时坐在 0,1 和 3 员工的旁边。
注意,公司也可以邀请员工 1,2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。
示例 2:
输入:favorite = [1,2,0]
输出:3
解释:
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示:
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。
示例 3: 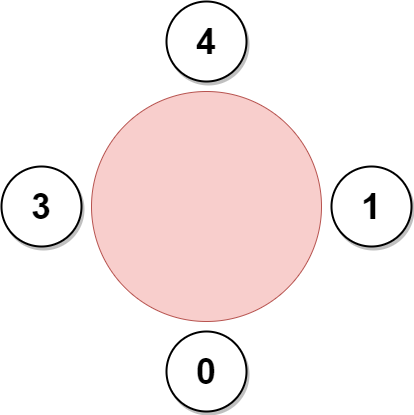
输入:favorite = [3,0,1,4,1]
输出:4
解释:
上图展示了公司可以邀请员工 0,1,3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加,因为他喜欢的员工 0 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。
提示:
内向基环树 + 拓扑排序
根据题意,圆形桌上 左右两边只要有一位是 所喜欢即可。
我们可从 向 添加有向边,从而得到一张包含多个「内向基环树」的图。
内向基环树,是指其满足基环树定义,且内向 bushi。
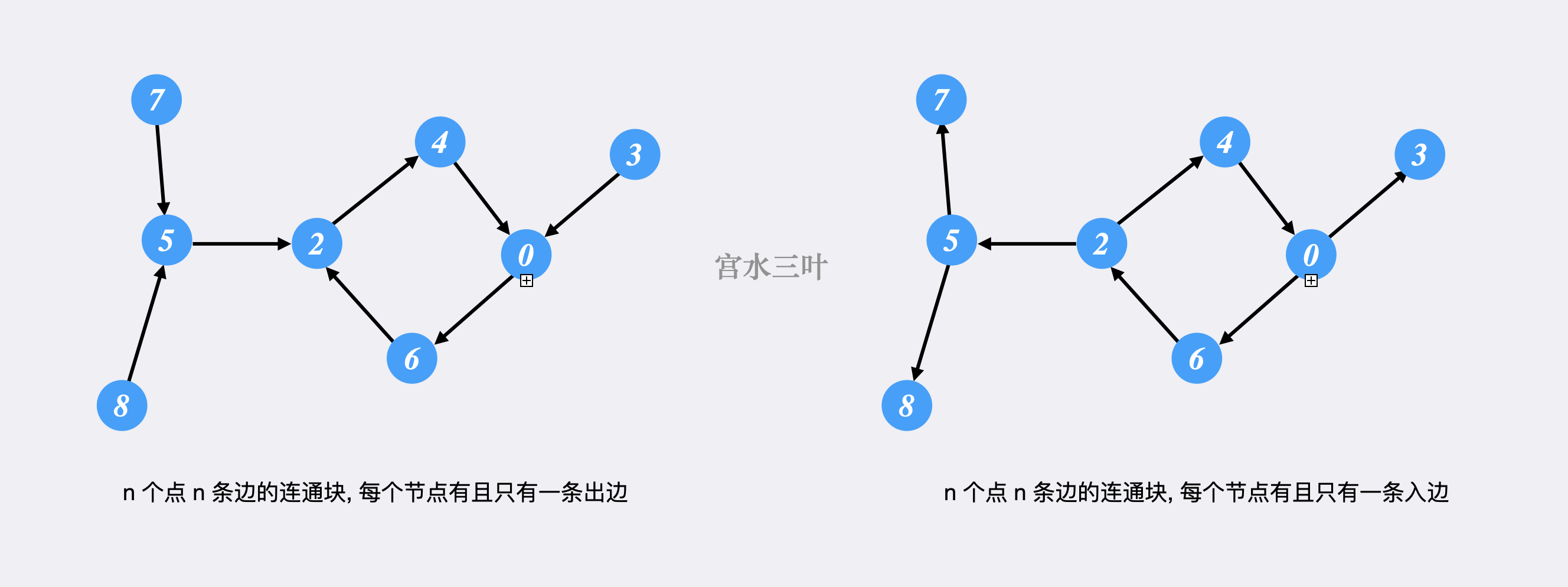
基环树是指其具有 个点 条边的联通块,而「内向」是指树中任意节点有且只有一条出边,对应的「外向」是指树中任意节点有且只有一条入边。
例如,左图内向,右图外向:
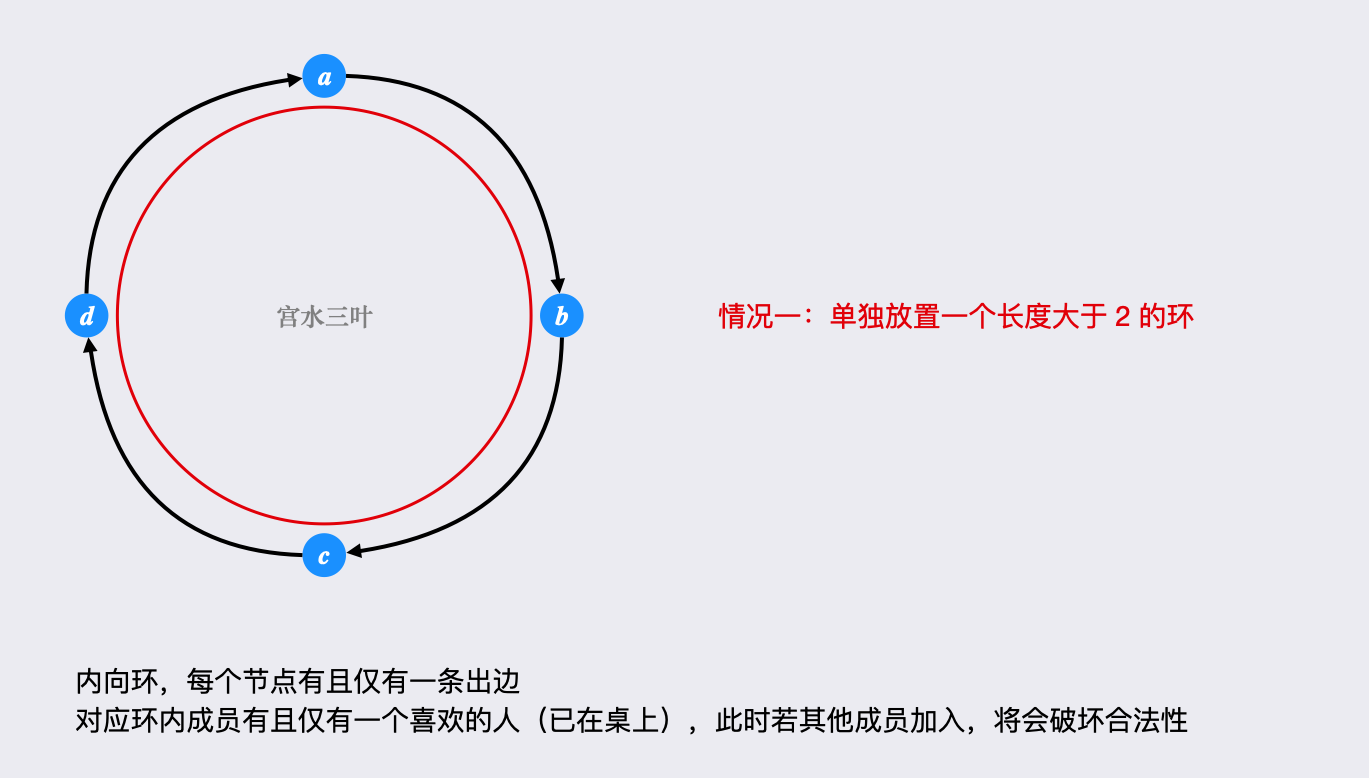
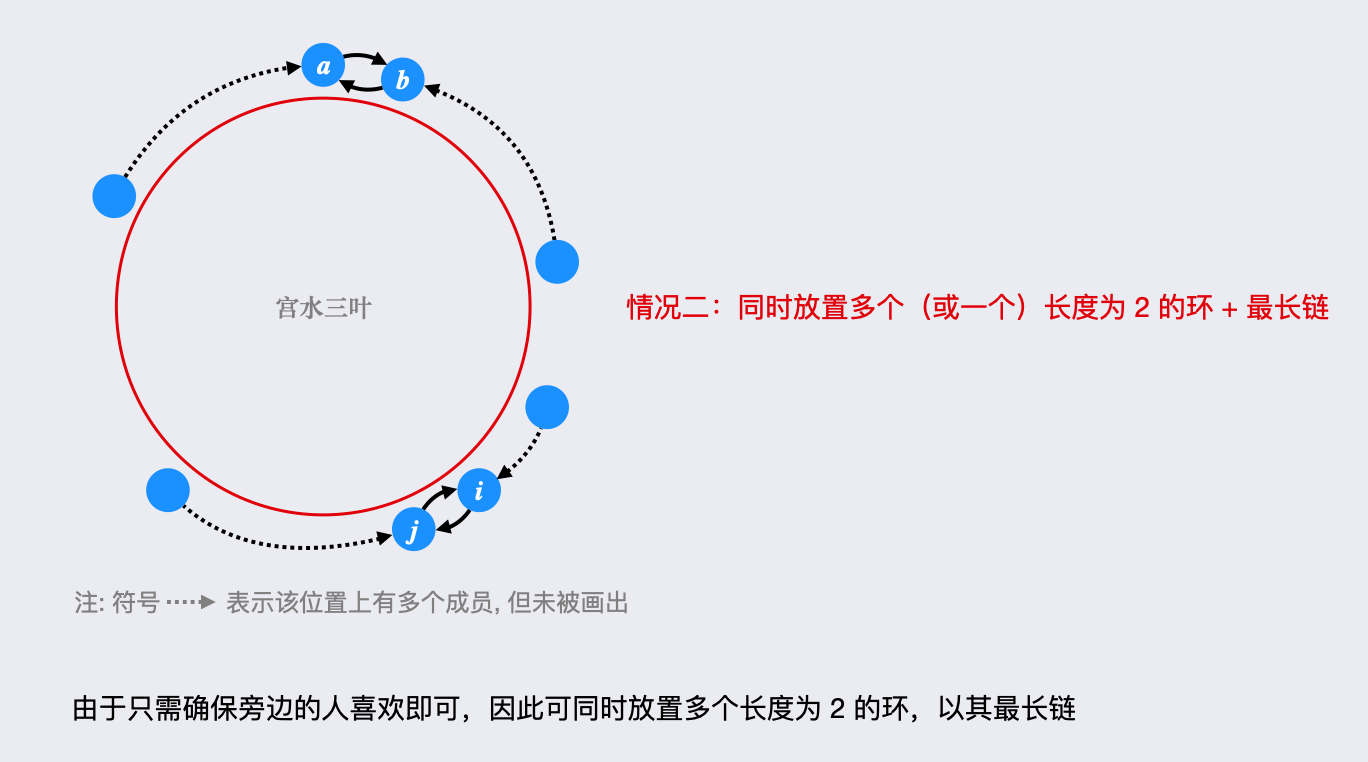
根据题意,「圆桌最多放置一个长度大于 的环(内向环,只有一条出边,即只有一个喜欢的人,安插其他非环成员,会破坏留下参加会议的必要条件),但可放置多个长度为 的环,且多个环可延伸出最长链(利用左右两侧只需有一个喜欢的人即满足)。」
在「取长度大于 的最大环」及「多个长度为 的环及其最长链之和」两者中取最大长度即是答案。
Java 代码:
class Solution {
public int maximumInvitations(int[] favorite) {
int n = favorite.length;
// in 统计每个节点的入度情况, max 统计节最长链
int[] in = new int[n], max = new int[n];
for (int x : favorite) in[x]++;
Deque<Integer> d = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
if (in[i] == 0) d.addLast(i);
}
// 拓扑排序: 求基环外的最长链
while (!d.isEmpty()) {
int cur = d.pollFirst(), ne = favorite[cur];
max[ne] = Math.max(max[ne], max[cur] + 1);
if (--in[ne] == 0) d.addLast(ne);
}
// 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
// 圆桌可放置多个等于 2 的环(ans2 累加该长度)
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
if (in[i] == 0) continue;
int j = favorite[i], cur = 1;
while (j != i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max[i] + max[favorite[i]];
else ans1 = Math.max(ans1, cur);
}
return Math.max(ans1, ans2);
}
}
Python 代码:
class Solution:
def maximumInvitations(self, favorite: List[int]) -> int:
n = len(favorite)
# in_degree 统计每个节点的入度情况, max_length 统计节最长链
in_degree, max_length = [0] * n, [0] * n
for x in favorite:
in_degree[x] += 1
d = deque()
for i in range(n):
if in_degree[i] == 0:
d.append(i)
# 拓扑排序: 求基环外的最长链
while d:
cur = d.popleft()
ne = favorite[cur]
max_length[ne] = max(max_length[ne], max_length[cur] + 1)
in_degree[ne] -= 1
if in_degree[ne] == 0:
d.append(ne)
# 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
# 圆桌可放置多个等于 2 的环(ans2 累加该长度)
ans1, ans2 = 0, 0
for i in range(n):
if in_degree[i] == 0:
continue
j, cur = favorite[i], 1
while j != i:
# 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in_degree[j] = 0
j = favorite[j]
cur += 1
if cur == 2:
ans2 += 2 + max_length[i] + max_length[favorite[i]]
else:
ans1 = max(ans1, cur)
return max(ans1, ans2)
C++ 代码:
class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
int n = favorite.size();
// in 统计每个节点的入度情况, max_length 统计节最长链
vector<int> in(n, 0);
vector<int> max_length(n, 0);
for (int x : favorite) in[x]++;
deque<int> d;
for (int i = 0; i < n; i++) {
if (in[i] == 0) d.push_back(i);
}
// 拓扑排序: 求基环外的最长链
while (!d.empty()) {
int cur = d.front();
d.pop_front();
int ne = favorite[cur];
max_length[ne] = max(max_length[ne], max_length[cur] + 1);
if (--in[ne] == 0) d.push_back(ne);
}
// 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
// 圆桌可放置多个等于 2 的环(ans2 累加该长度)
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
if (in[i] == 0) continue;
int j = favorite[i], cur = 1;
while (j != i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max_length[i] + max_length[favorite[i]];
else ans1 = max(ans1, cur);
}
return max(ans1, ans2);
}
};
TypeScript 代码:
function maximumInvitations(favorite: number[]): number {
const n = favorite.length;
// in_degree 统计每个节点的入度情况, max_length 统计节最长链
const in_degree = Array(n).fill(0), max_length = Array(n).fill(0);
for (const x of favorite) in_degree[x]++;
const d = [];
for (let i = 0; i < n; i++) {
if (in_degree[i] === 0) d.push(i);
}
// 拓扑排序: 求基环外的最长链
while (d.length > 0) {
const cur = d.shift() as number;
const ne = favorite[cur];
max_length[ne] = Math.max(max_length[ne], max_length[cur] + 1);
if (--in_degree[ne] === 0) d.push(ne);
}
// 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
// 圆桌可放置多个等于 2 的环(ans2 累加该长度)
let ans1 = 0, ans2 = 0;
for (let i = 0; i < n; i++) {
if (in_degree[i] === 0) continue;
let j = favorite[i], cur = 1;
while (j !== i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in_degree[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max_length[i] + max_length[favorite[i]];
else ans1 = Math.max(ans1, cur);
}
return Math.max(ans1, ans2);
};
-
时间复杂度:统计入度的复杂度为 ;拓扑排序求最长链复杂度为 ;计算答案过程中,每个点最多被访问两次(环内节点),复杂度为 。整体复杂度为 -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2217 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉