文章目录
- 引子
- 生成问题回顾:Generator
- Math Background
- Jacobian Matrix
- Determinant 行列式
- Change of Variable Theorem
- 简单实例
- 一维实例
- 二维实例
- 网络G的限制
- 基于Flow的网络构架
- G的训练
- Coupling Layer
- Coupling Layer反函数计算
- Coupling Layer Jacobian矩阵计算
- Coupling Layer Stacking
- 1×1 Convolution
- GLOW效果
- 其他工作
原视频见油管https://www.youtube.com/watch?v=uXY18nzdSsM
Latex编辑器
引子
之前有讲过三种生成模型:
1.Component-by-component (也叫:Auto-regressive Model):按component进行生成,如何确定最佳的生成顺序?而且一个个的生成会使得速度比较慢。特别是语音生成,一秒钟需要生成的采样点个数约为20万个,有人声称:生成一秒钟,合成90分。
2.Autoencoder(VAE):这个模型证明了是在优化似然的Lower bound,而非去maximize似然,这样的效果有多好还不好说。
3.Generative Adversarial Network(GAN):虽然很强,但是很难训练。
生成问题回顾:Generator
A generator G G G is a network. The network defines a probability distribution p G p_G pG
为什么说生成器网络定义了一个概率分布?看下面的流程:
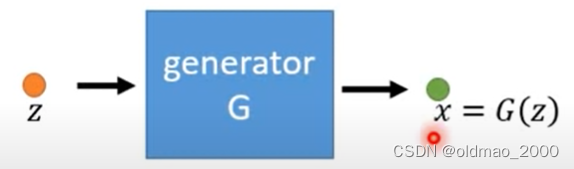
图中 G G G吃一个向量 z z z得到一个表示 x = G ( z ) x=G(z) x=G(z),这个 x x x是一个高维向量,是一张图像, x x x里面每一个维度就是这个图像的每一个像素。
输入向量 z z z是用一个Normal Distribution中采样得来的:
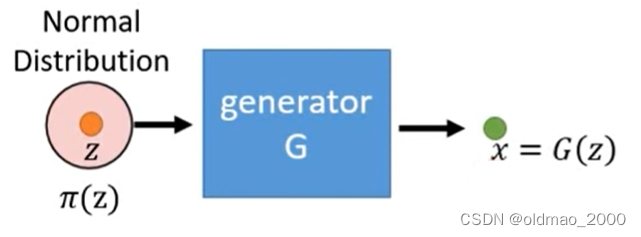
因此经过多次采样经过 G G G后会得到一个比较复杂的分布 p G p_G pG:
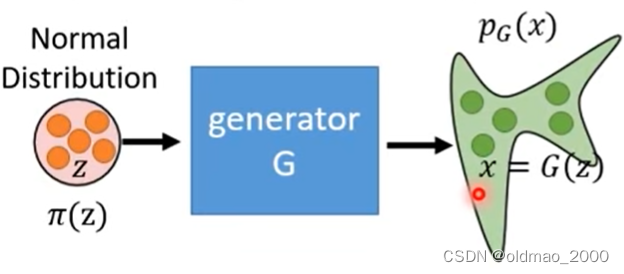
我们希望找到一个 G G G,使得其生成的分布 p G p_G pG与实际图像分布 p d a t a ( x ) p_{data}(x) pdata(x)越接近越好。
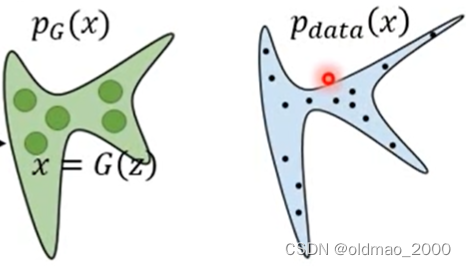
越接近越好就是要求最大似然,也就是要使得 p G ( x ) p_G(x) pG(x)的似然与 p d a t a ( x ) p_{data}(x) pdata(x)采样得到的样本越接近越好,用数学表示为:
G ∗ = a r g max G ∑ i = 1 m log p G ( x i ) , { x 1 , x 2 , ⋯ , x m } f r o m p d a t a ( x ) ≈ a r g min G K L ( p d a t a ∣ ∣ p G ) \begin{aligned} G^*&=arg\max_G\sum_{i=1}^{m}\log p_G(x^i),\{x^1,x^2,\cdots,x^m\}\text{ } from\text{ } p_{data}(x)\\ &\approx arg\min_G KL(p_{data}||p_G)\end{aligned} G∗=argGmaxi=1∑mlogpG(xi),{x1,x2,⋯,xm} from pdata(x)≈argGminKL(pdata∣∣pG)
上式中的求两个概率越接近越好也相当于求他们的KL散度越小越好。
由于 G G G是一个网络,因此其生成概率的最大似然非常难求,Flow-based Generative Model提出了一种可以直接求最大似然的方法,接下来进入难点,补充部分数学推导。
Math Background
三个东西:Jacobian, Determinant, Change of Variable Theorem
Jacobian Matrix
假如有一个函数 x = f ( z ) x=f(z) x=f(z),吃一个二维向量 z = [ z 1 z 2 ] z=\begin{bmatrix} z_1 \\ z_2 \end{bmatrix} z=[z1z2],得到输出: x = [ x 1 x 2 ] x=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} x=[x1x2]。(Jacobian Matrix的输入和输出维度不一定一样,这里先简化来举例)
这里的函数可以看做上面提到的生成器 G G G。
函数 x = f ( z ) x=f(z) x=f(z)的Jacobian Matrix J f J_f Jf可以写为输入和输出两两组合做偏导后形成的矩阵:
J f = [ ∂ x 1 ∂ z 1 ∂ x 1 ∂ z 2 ∂ x 2 ∂ z 1 ∂ x 2 ∂ z 2 ] (1) J_f=\begin{bmatrix} \cfrac{\partial x_1}{\partial z_1} & \cfrac{\partial x_1}{\partial z_2}\\ \cfrac{\partial x_2}{\partial z_1} &\cfrac{\partial x_2}{\partial z_2} \end{bmatrix}\tag1 Jf= ∂z1∂x1∂z1∂x2∂z2∂x1∂z2∂x2 (1)
Jacobian Matrix小例子,假如有这样的函数:
[ z 1 + z 2 2 z 2 ] = f ( [ z 1 z 2 ] ) \begin{bmatrix} z_1+z_2 \\ 2z_2 \end{bmatrix}=f\left(\begin{bmatrix} z_1 \\ z_2 \end{bmatrix}\right) [z1+z22z2]=f([z1z2])
则根据上面的公式1可以求得:
J f = [ ∂ ( z 1 + z 2 ) ∂ z 1 ∂ ( z 1 + z 2 ) ∂ z 2 ∂ 2 z 2 ∂ z 1 ∂ 2 z 2 ∂ z 2 ] = [ 1 1 2 0 ] J_f=\begin{bmatrix} \cfrac{\partial (z_1+z_2)}{\partial z_1} & \cfrac{\partial (z_1+z_2)}{\partial z_2}\\ \cfrac{\partial 2z_2}{\partial z_1} &\cfrac{\partial 2z_2}{\partial z_2} \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 2 &0 \end{bmatrix} Jf= ∂z1∂(z1+z2)∂z1∂2z2∂z2∂(z1+z2)∂z2∂2z2 =[1210]
同理,若有 z = f − 1 ( x ) z=f^{-1}(x) z=f−1(x),则有函数 f f finverse 的Jacobian Matrix:
J f − 1 = [ ∂ z 1 ∂ x 1 ∂ z 1 ∂ x 2 ∂ z 2 ∂ x 1 ∂ z 2 ∂ x 2 ] (2) J_{f^{-1}}=\begin{bmatrix} \cfrac{\partial z_1}{\partial x_1} & \cfrac{\partial z_1}{\partial x_2}\\ \cfrac{\partial z_2}{\partial x_1} &\cfrac{\partial z_2}{\partial x_2} \end{bmatrix}\tag2 Jf−1= ∂x1∂z1∂x1∂z2∂x2∂z1∂x2∂z2 (2)
公式1和2的两个矩阵互逆,二者的乘积结果是Identity矩阵(对角线是1,其他都是0)。
反函数的Jacobian Matrix小例子,假如有这样的函数:
[ x 2 / 2 x 1 − x 2 / 2 ] = f − 1 ( [ x 1 x 2 ] ) \begin{bmatrix} x_2/2 \\ x_1-x_2/2 \end{bmatrix}=f^{-1}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\right) [x2/2x1−x2/2]=f−1([x1x2])
则根据上面的公式2可以求得:
J f − 1 = [ ∂ ( x 2 / 2 ) ∂ x 1 ∂ ( x 2 / 2 ) ∂ x 2 ∂ ( x 1 − x 2 / 2 ) ∂ x 1 ∂ ( x 1 − x 2 / 2 ) ∂ x 2 ] = [ 0 1 / 2 1 − 1 / 2 ] J_{f^{-1}}=\begin{bmatrix} \cfrac{\partial (x_2/2)}{\partial x_1} & \cfrac{\partial (x_2/2)}{\partial x_2}\\ \cfrac{\partial (x_1-x_2/2)}{\partial x_1} &\cfrac{\partial (x_1-x_2/2)}{\partial x_2} \end{bmatrix}=\begin{bmatrix} 0 & 1/2\\ 1 &-1/2 \end{bmatrix} Jf−1= ∂x1∂(x2/2)∂x1∂(x1−x2/2)∂x2∂(x2/2)∂x2∂(x1−x2/2) =[011/2−1/2]
两个小例子的结果相乘:
J f J f − 1 = [ 1 1 2 0 ] [ 0 1 / 2 1 − 1 / 2 ] = I J_fJ_{f^{-1}}=\begin{bmatrix} 1 & 1\\ 2 &0 \end{bmatrix}\begin{bmatrix} 0 & 1/2\\ 1 &-1/2 \end{bmatrix}=I JfJf−1=[1210][011/2−1/2]=I
Determinant 行列式
The determinant of a square matrix is a scalar that provides information about the matrix.
对于2×2的矩阵:
A = [ a b c d ] A=\begin{bmatrix} a&b \\ c &d \end{bmatrix} A=[acbd]
有:
d e t ( A ) = a d − b c det(A)=ad-bc det(A)=ad−bc
对于3×3的矩阵:
[ a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 ] \begin{bmatrix} a_1 & a_2& a_3\\ a_4 & a_ 5&a_6 \\ a_7 & a_8 &a_9 \end{bmatrix} a1a4a7a2a5a8a3a6a9
有:
d e t ( A ) = a 1 a 5 a 9 + a 2 a 6 a 7 + a 3 a 4 a 8 − a 3 a 5 a 7 − a 2 a 4 a 9 − a 1 a 6 a 8 det(A)=a_1a_5a_9+a_2a_6a_7+a_3a_4a_8-a_3a_5a_7-a_2a_4a_9-a_1a_6a_8 det(A)=a1a5a9+a2a6a7+a3a4a8−a3a5a7−a2a4a9−a1a6a8
行列式性质:
d e t ( A ) = 1 d e t ( A − 1 ) det(A)=\cfrac{1}{det(A^{-1})} det(A)=det(A−1)1
对于Jacobian Matrix则有:
d e t ( J f ) = 1 d e t ( J f − 1 ) det(J_f)=\cfrac{1}{det(J_{f^{-1}})} det(Jf)=det(Jf−1)1
行列式的几何含义是指行向量在高维空间形成的体积。对于低维,例如下面2×2的矩阵,其行列式就对应了其行向量所形成的面积

对于3×3的矩阵,,其行列式就对应了其行向量所形成的体积
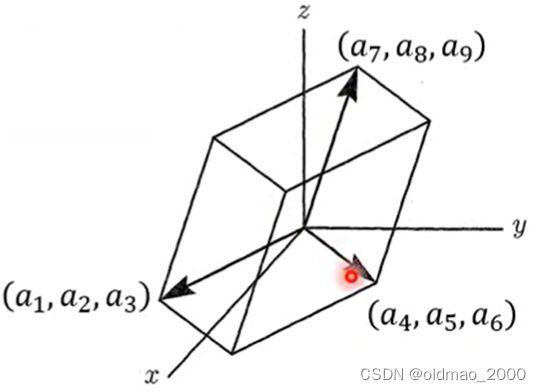
Change of Variable Theorem
变量变换定理。
简单实例
假设有分布 π ( z ) \pi(z) π(z),其图像如下:
另有函数可以以上面的分布作为输入 x = f ( z ) x=f(z) x=f(z),得到的结果是另外一个分布 p ( x ) p(x) p(x),其图像如下:
现在要弄清楚 π ( z ) \pi(z) π(z)和 p ( x ) p(x) p(x)两个分布之间的关系。
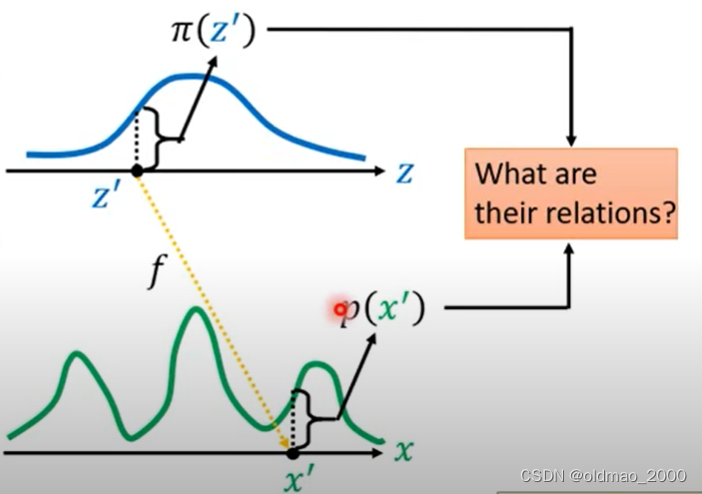
下面来看简单的例子,假设分布 π ( z ) \pi(z) π(z)如下图:
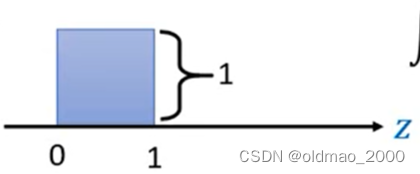
可以看到 π ( z ) \pi(z) π(z)是一个简单的均匀分布,它在0~1之间有分布。根据概率的定义:
∫ 0 1 π ( z ) d z = 1 \int_0^1\pi(z)dz=1 ∫01π(z)dz=1
因此可以知道该分布的高度为1。
令假设有函数
x = f ( z ) = 2 z + 1 x=f(z)=2z+1 x=f(z)=2z+1
则可以得到函数生成的分布 p ( x ) p(x) p(x)的图像为:
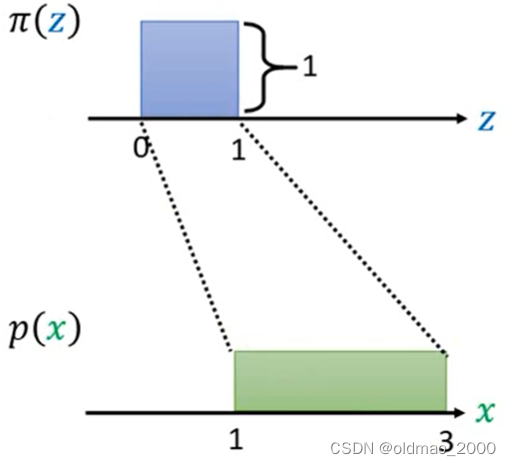
由于 p ( x ) p(x) p(x)是概率分布,因此其也要满足:
∫ 1 3 p ( x ) d x = 1 \int_1^3p(x)dx=1 ∫13p(x)dx=1
则绿色分布的高度为0.5,则可以德奥两个分布之间的关系:
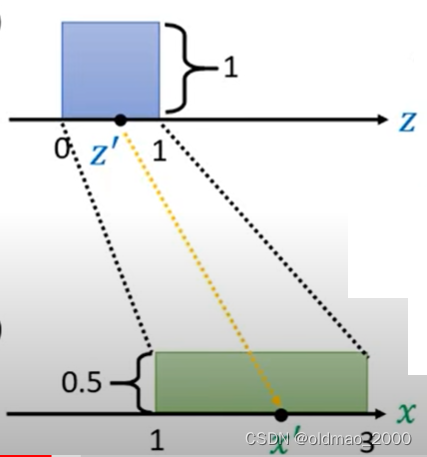
可以写成:
p ( x ′ ) = 1 2 π ( z ′ ) p(x')=\cfrac{1}{2}\pi(z') p(x′)=21π(z′)
一维实例
下面再推广到更一般的情况。
现在有一个分布记为 π ( z ) \pi(z) π(z),它经过一个变换(或者按上面的说法经过一个函数)后,得到另外一个分布 p ( x ) p(x) p(x),对于下图而言, z ′ z' z′通过变换后就到 x ′ x' x′的位置,对应的概率密度从 π ( z ′ ) \pi(z') π(z′)变成了 p ( x ′ ) p(x') p(x′)。
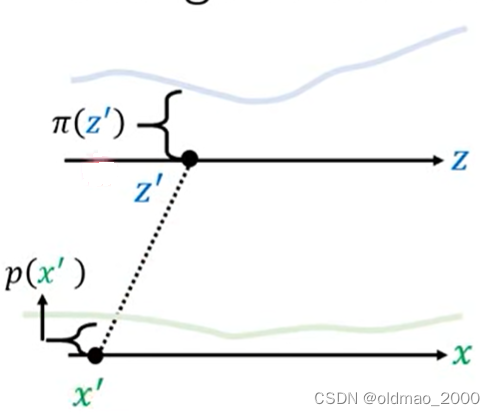
虽然我们不知道 π ( z ) \pi(z) π(z)和 p ( x ) p(x) p(x)具体的公式,但是我们如果知道变换所涉及的函数,是可以写出二者的关系的,这就是通过Change of Variable Theorem来找到这个关系的过程。
先将 z ′ z' z′做一个小小的变动,成为: z ′ + Δ z z'+\Delta z z′+Δz,相应的,根据变换函数,可以得到对应的 x ′ + Δ x x'+\Delta x x′+Δx
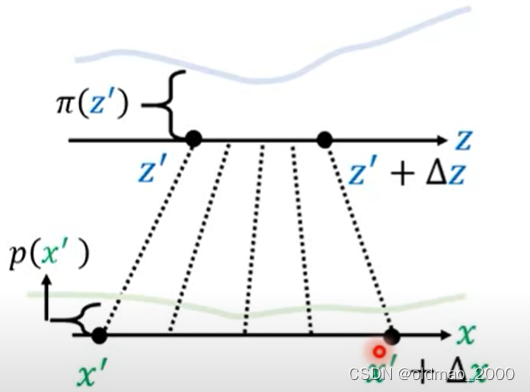
由于我们做的小小的变动,因此,从 z ′ z' z′到 z ′ + Δ z z'+\Delta z z′+Δz对应的概率密度可以看做是均匀分布,同理,从 x ′ x' x′到 x ′ + Δ x x'+\Delta x x′+Δx应的概率密度也可以看做是均匀分布:
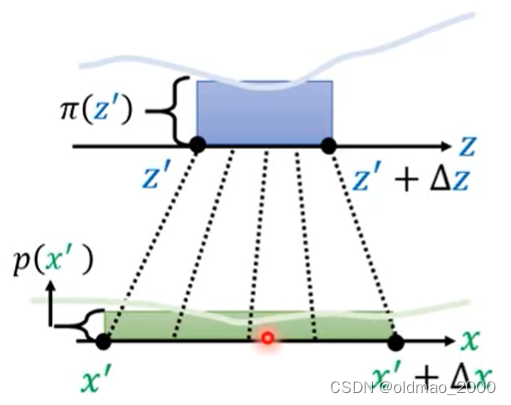
相当于将蓝色方块经过变形,得到绿色方块,二者的面积是相等的,二者长×宽应该结果一样。即:
p ( x ′ ) Δ x = π ( z ′ ) Δ z p(x')\Delta x=\pi(z')\Delta z p(x′)Δx=π(z′)Δz
移项办得到二者的关系可以写为:
p ( x ′ ) = π ( z ′ ) Δ z Δ x p(x')=\pi(z')\cfrac{\Delta z}{\Delta x} p(x′)=π(z′)ΔxΔz
由于 Δ \Delta Δ是很小的值,因此根据导数的概念,上式可以写为:
p ( x ′ ) = π ( z ′ ) d z d x p(x')=\pi(z')\cfrac{d z}{d x} p(x′)=π(z′)dxdz
由于上面的求导项可能有正负:
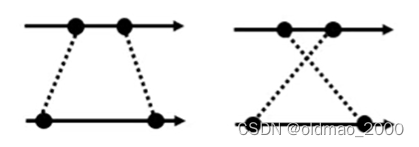
因此要加上绝对值避免负值:
p ( x ′ ) = π ( z ′ ) ∣ d z d x ∣ p(x')=\pi(z')\left|\cfrac{d z}{d x}\right| p(x′)=π(z′) dxdz
二维实例
对于二维的情况:
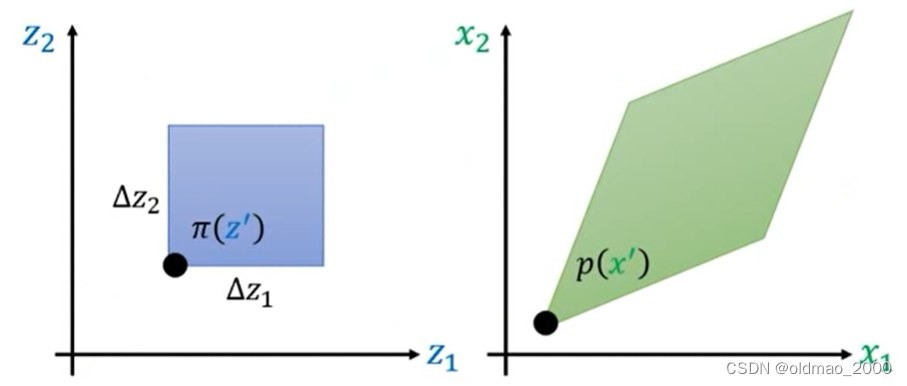
同样的,现在有一个分布记为 π ( z ) \pi(z) π(z),它经过一个变换后,得到另外一个分布 p ( x ) p(x) p(x),对于下图而言, z ′ z' z′通过变换后就到 x ′ x' x′的位置,对应的概率密度从 π ( z ′ ) \pi(z') π(z′)变成了 p ( x ′ ) p(x') p(x′)。
还是给 z ′ z' z′做一个小小的变动,蓝色方形和绿色菱形的对应的概率密度体积应该相等。这里的体积就是底面积×概率密度,蓝色底面积好求,绿色菱形底面积用上面的行列式的几何概念来求,可以看到下图中菱形可以写为成两个向量的表示 [ Δ x 11 , Δ x 21 ] [\Delta x_{11}, \Delta x_{21}] [Δx11,Δx21], [ Δ x 12 , Δ x 22 ] [\Delta x_{12},\Delta x_{22}] [Δx12,Δx22]。

最后就是写成:
p ( x ′ ) ∣ d e t [ Δ x 11 Δ x 21 Δ x 12 Δ x 22 ] ∣ = π ( z ′ ) Δ z 1 Δ z 2 (3) p(x')\left| det\begin{bmatrix} \Delta x_{11}&\Delta x_{21} \\ \Delta x_{12} &\Delta x_{22} \end{bmatrix} \right|=\pi(z')\Delta z_{1}\Delta z_{2}\tag3 p(x′) det[Δx11Δx12Δx21Δx22] =π(z′)Δz1Δz2(3)
下面开始数学上的化简,假设变换函数为: x = f ( z ) x=f(z) x=f(z),则公式3可以写为:
p ( x ′ ) ∣ 1 Δ z 1 Δ z 2 d e t [ Δ x 11 Δ x 21 Δ x 12 Δ x 22 ] ∣ = π ( z ′ ) p(x')\left|\cfrac{1}{\Delta z_{1}\Delta z_{2}} det\begin{bmatrix} \Delta x_{11}&\Delta x_{21} \\ \Delta x_{12} &\Delta x_{22} \end{bmatrix} \right|=\pi(z') p(x′) Δz1Δz21det[Δx11Δx12Δx21Δx22] =π(z′)
根据线代的指数,将分数项放入行列式:
p ( x ′ ) ∣ d e t [ Δ x 11 Δ z 1 Δ x 21 Δ z 1 Δ x 12 Δ z 2 Δ x 22 Δ z 2 ] ∣ = π ( z ′ ) p(x')\left|det\begin{bmatrix} \cfrac{\Delta x_{11}}{\Delta z_1} &\cfrac{\Delta x_{21}}{\Delta z_1} \\ \cfrac{\Delta x_{12}}{\Delta z_2} &\cfrac{\Delta x_{22}}{\Delta z_2} \end{bmatrix} \right|=\pi(z') p(x′) det Δz1Δx11Δz2Δx12Δz1Δx21Δz2Δx22 =π(z′)
由于:
Δ x 11 \Delta x_{11} Δx11是 Δ z 1 \Delta z_{1} Δz1在 x 1 x_1 x1上的改变量;
Δ x 21 \Delta x_{21} Δx21是 Δ z 1 \Delta z_{1} Δz1在 x 2 x_2 x2上的改变量;
Δ x 12 \Delta x_{12} Δx12是 Δ z 2 \Delta z_{2} Δz2在 x 1 x_1 x1上的改变量;
Δ x 22 \Delta x_{22} Δx22是 Δ z 2 \Delta z_{2} Δz2在 x 2 x_2 x2上的改变量。
上面的式子可以写成:
p ( x ′ ) ∣ d e t [ ∂ x 1 ∂ z 1 ∂ x 2 ∂ z 1 ∂ x 1 ∂ z 2 ∂ x 2 ∂ z 2 ] ∣ = π ( z ′ ) p(x')\left|det\begin{bmatrix} \cfrac{\partial x_{1}}{\partial z_1} &\cfrac{\partial x_{2}}{\partial z_1} \\ \cfrac{\partial x_{1}}{\partial z_2} &\cfrac{\partial x_{2}}{\partial z_2} \end{bmatrix} \right|=\pi(z') p(x′) det ∂z1∂x1∂z2∂x1∂z1∂x2∂z2∂x2 =π(z′)
将矩阵进行Transpose不会改变行列式的值,上式可以写成:
p ( x ′ ) ∣ d e t [ ∂ x 1 ∂ z 1 ∂ x 1 ∂ z 2 ∂ x 2 ∂ z 1 ∂ x 2 ∂ z 2 ] ∣ = π ( z ′ ) p(x')\left|det\begin{bmatrix} \cfrac{\partial x_{1}}{\partial z_1} &\cfrac{\partial x_{1}}{\partial z_2} \\ \cfrac{\partial x_{2}}{\partial z_1} &\cfrac{\partial x_{2}}{\partial z_2} \end{bmatrix} \right|=\pi(z') p(x′) det ∂z1∂x1∂z1∂x2∂z2∂x1∂z2∂x2 =π(z′)
上面行列式中的句子和公式1中的Jacobian Matrix形式一样,因此可以写成:
p ( x ′ ) ∣ d e t ( J f ) ∣ = π ( z ′ ) (4) p(x')\left|det(J_f) \right|=\pi(z')\tag4 p(x′)∣det(Jf)∣=π(z′)(4)
也可以写为:
p ( x ′ ) = π ( z ′ ) ∣ 1 d e t ( J f ) ∣ = π ( z ′ ) ∣ d e t ( J f − 1 ) ∣ (5) p(x')=\pi(z')\left|\cfrac{1}{det(J_f) }\right|=\pi(z')|det(J_{f^{-1}})| \tag5 p(x′)=π(z′) det(Jf)1 =π(z′)∣det(Jf−1)∣(5)
网络G的限制
先把上面最大似然的式子copy下来
G ∗ = a r g max G ∑ i = 1 m log p G ( x i ) , { x 1 , x 2 , ⋯ , x m } f r o m P d a t a ( x ) G^*=arg\max_G\sum_{i=1}^{m}\log p_G(x^i),\{x^1,x^2,\cdots,x^m\}\text{ } from\text{ } P_{data}(x) G∗=argGmaxi=1∑mlogpG(xi),{x1,x2,⋯,xm} from Pdata(x)
根据上面公式5,可以把 p G p_G pG写成:
p G ( x i ) = π ( z i ) ∣ d e t ( J G − 1 ) ∣ p_G(x^i)=\pi (z^i)|det(J_{G^{-1}})| pG(xi)=π(zi)∣det(JG−1)∣
由已知的 x = G ( z ) x=G(z) x=G(z)可以得其反函数为: z i = G − 1 ( x i ) z^i=G^{-1}(x^i) zi=G−1(xi),带入上式:
p G ( x i ) = π ( G − 1 ( x i ) ) ∣ d e t ( J G − 1 ) ∣ p_G(x^i)=\pi \left(G^{-1}(x^i)\right )\left|det(J_{G^{-1}})\right | pG(xi)=π(G−1(xi))∣det(JG−1)∣
两边同时取对数,然后乘变加展开:
log p G ( x i ) = log [ π ( G − 1 ( x i ) ) ∣ d e t ( J G − 1 ) ∣ ] = log ( G − 1 ( x i ) ) + log ∣ d e t ( J G − 1 ) ∣ \begin{aligned} \log p_G(x^i)&=\log \left[\pi \left(G^{-1}(x^i)\right )\left|det(J_{G^{-1}})\right |\right]\\ &= \log \left(G^{-1}(x^i)\right )+\log\left|det(J_{G^{-1}})\right |\end{aligned} logpG(xi)=log[π(G−1(xi))∣det(JG−1)∣]=log(G−1(xi))+log∣det(JG−1)∣
要求 G ∗ G^* G∗就是要求上式的最大值,如果要想用GD来求解,必须要计算两个东西:
1. d e t ( J G − 1 ) 或 d e t ( J G ) det(J_{G^{-1}})或det(J_{G}) det(JG−1)或det(JG):这个还比较好算,就是要计算输入 z z z和输出 x x x的偏导即可,但是如果输入和输出各自有1000维,由于Jacobian Matrix是输入输出的各个维度的两两偏导,其大小就是:1000×1000,这个大小的矩阵求行列式的值计算量会很大。
2. G − 1 G^{-1} G−1:主要是要确保 G G G有反函数,由于 G G G是一个网络,因此其构架要精心设计才会有反函数。
根据上面的两点,如果要输出一张100×100×3的图片,那么输入也要100×100×3,这个是确保 G G G有反函数的必要条件。
显然,网络 G G G不可以是简单的、任意的类似CNN、RNN等网络架构,于是就有了流式设计。
基于Flow的网络构架
一个网络 G G G不够,因此考虑像流水一样设计多个网络进行concat:

根据上面的公式,这些网络之间的输入输出关系如下:
p 1 ( x i ) = π ( z i ) ( ∣ d e t ( J G 1 − 1 ) ∣ ) p 2 ( x i ) = π ( z i ) ( ∣ d e t ( J G 1 − 1 ) ∣ ) ( ∣ d e t ( J G 2 − 1 ) ∣ ) ⋮ p K ( x i ) = π ( z i ) ( ∣ d e t ( J G 1 − 1 ) ∣ ) ⋯ ( ∣ d e t ( J G K − 1 ) ∣ ) \begin{aligned} p_1(x^i)&=\pi \left(z^i\right )\left(\left|det(J_{G^{-1}_1})\right |\right )\\ p_2(x^i)&=\pi \left(z^i\right )\left(\left|det(J_{G^{-1}_1})\right |\right )\left(\left|det(J_{G^{-1}_2})\right |\right )\\ &\quad\vdots\\ p_K(x^i)&=\pi \left(z^i\right )\left(\left|det(J_{G^{-1}_1})\right |\right )\cdots\left(\left|det(J_{G^{-1}_K})\right |\right ) \end{aligned} p1(xi)p2(xi)pK(xi)=π(zi)( det(JG1−1) )=π(zi)( det(JG1−1) )( det(JG2−1) )⋮=π(zi)( det(JG1−1) )⋯( det(JGK−1) )
两边同时取对数,乘变加:
log p K ( x i ) = log π ( z i ) + ∑ h = 1 K log ∣ d e t ( J G K − 1 ) ∣ (6) \log p_K(x^i)=\log \pi \left(z^i\right )+\sum_{h=1}^K\log\left|det(J_{G^{-1}_K})\right |\tag6 logpK(xi)=logπ(zi)+h=1∑Klog det(JGK−1) (6)
其中:
z i = G 1 − 1 ( ⋯ G K − 1 ( x i ) ) z^i=G^{-1}_1\left(\cdots G^{-1}_K\left(x^i\right )\right ) zi=G1−1(⋯GK−1(xi))
现在要求的就是公式6的最大化。
G的训练
为了求公式6的最大化,这里先简化一下问题,先考虑只有一个 G G G情况:
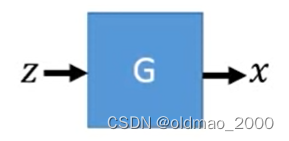
此时需要最大化的式子为:
log p G ( x i ) = log π ( G − 1 ( x i ) ) + log ∣ d e t ( J G − 1 ) ∣ (7) \log p_G(x^i)=\log \pi \left(G^{-1}\left(x^i\right )\right )+\log\left|det(J_{G^{-1}})\right |\tag7 logpG(xi)=logπ(G−1(xi))+log∣det(JG−1)∣(7)
式子中只有出现 G − 1 G^{-1} G−1,因此可以训练一个 G − 1 G^{-1} G−1对应的网络,训练好后,将其输入输出反过来,就变成了 G G G。
具体训练过程是从真实数据 p d a t a ( x ) p_{data}(x) pdata(x)中采样一些样本 x i x^i xi出来,丢进 G − 1 G^{-1} G−1对应的网络,得到对应的 z i z^i zi
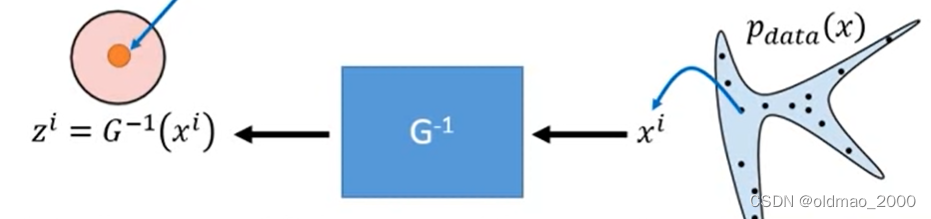
先看公式7中的前半部分:
log π ( G − 1 ( x i ) ) \log \pi \left(G^{-1}\left(x^i\right )\right ) logπ(G−1(xi))
这里的 π \pi π是正态分布,也就是当 z i = G − 1 ( x i ) = 0 z^i=G^{-1}\left(x^i\right )=0 zi=G−1(xi)=0的时候,正态分布 π \pi π会得到最大值(正态分布最正中的地方就是波峰);
如果 z i z^i zi趋向于0或者说0向量的时候,其对应的Jacobian Matrix, J G − 1 J_{G^{-1}} JG−1也会是0矩阵(因为该矩阵每个元素都是要求 z z z对 x x x的偏导),0矩阵的行列式 d e t ( J G − 1 ) = 0 det(J_{G^{-1}})=0 det(JG−1)=0,再取对数会使得公式7中的后半部分趋向于负无穷大。
总之就是一项要使得 z i z^i zi趋向于0,后一项使得 z i z^i zi不为0。
Coupling Layer
Coupling Layer反函数计算
这个设计可以参考两篇文章:NICE: Non-linear Independent Components Estimation、Density estimation using Real NVP
具体结构如下图:
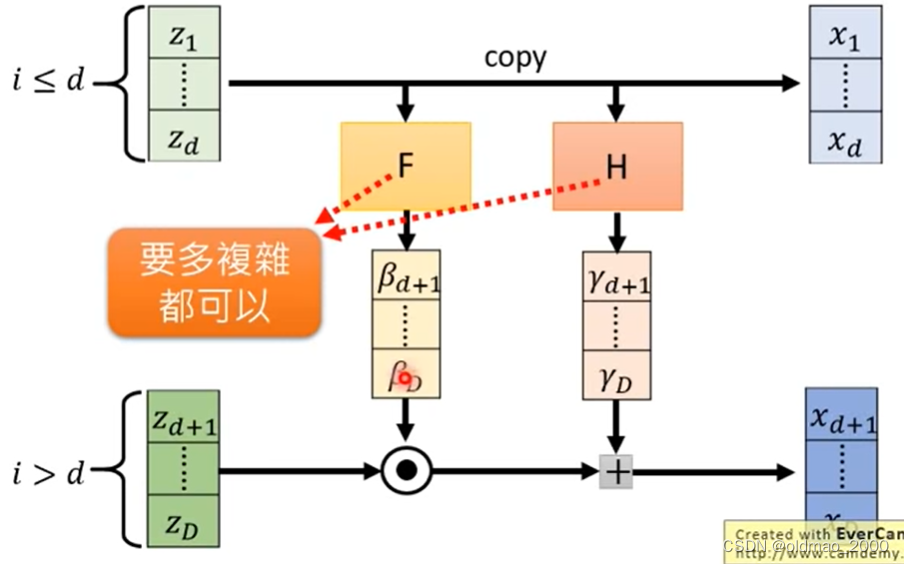
假设 z z z是 D D D维,先将其分成两部分,分别是: z 1 , ⋯ , z d z_1,\cdots,z_d z1,⋯,zd和 z d + 1 , ⋯ , z D z_{d+1},\cdots,z_D zd+1,⋯,zD。
1.将 z z z的第一部分 z 1 , ⋯ , z d z_1,\cdots,z_d z1,⋯,zd直接复制,成为 x x x的第一部分: x 1 , ⋯ , x d x_1,\cdots,x_d x1,⋯,xd;
2.将 z z z的第一部分 z 1 , ⋯ , z d z_1,\cdots,z_d z1,⋯,zd分别丢进两个网络 F F F和 H H H(两个网络没有invertiable的限制,可以是深度CNN),分别得到 β d + 1 , ⋯ , β D \beta_{d+1},\cdots,\beta_D βd+1,⋯,βD和 γ d + 1 , ⋯ , γ D \gamma_{d+1},\cdots,\gamma_D γd+1,⋯,γD;
3.将 z z z的第二部分 z d + 1 , ⋯ , z D z_{d+1},\cdots,z_D zd+1,⋯,zD先和 β d + 1 , ⋯ , β D \beta_{d+1},\cdots,\beta_D βd+1,⋯,βD点积,然后再加上 γ d + 1 , ⋯ , γ D \gamma_{d+1},\cdots,\gamma_D γd+1,⋯,γD,得到 x x x的第二部分: x d + 1 , ⋯ , x D x_{d+1},\cdots,x_D xd+1,⋯,xD:
x i > d = β i z i + γ i x_{i>d}=\beta_iz_i+\gamma_i xi>d=βizi+γi
Coupling Layer之所以这样设计,就是可以计算反函数,现在利用 x x x来算 z z z,看下图的红线及序号:
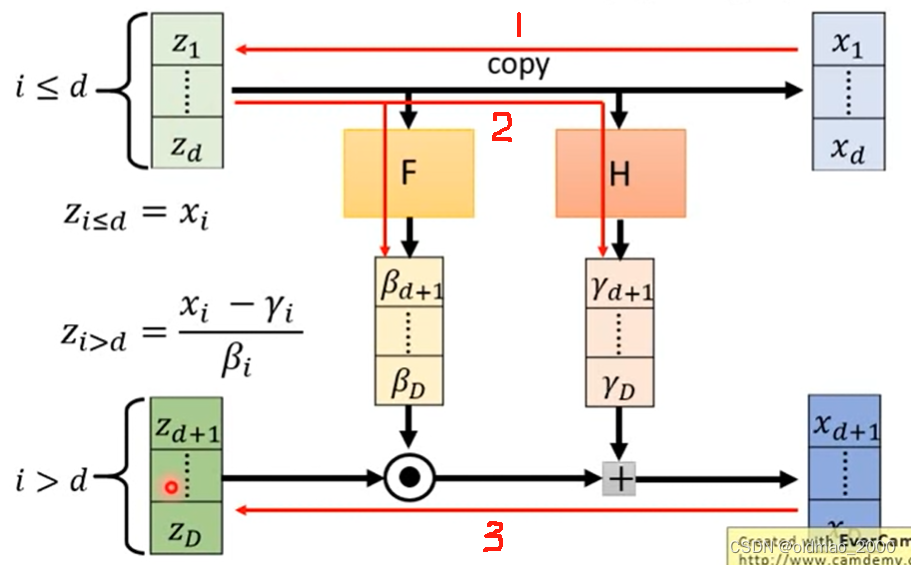
1.将 x x x的第一部分: x 1 , ⋯ , x d x_1,\cdots,x_d x1,⋯,xd直接复制,成为 z z z的第一部分 z 1 , ⋯ , z d z_1,\cdots,z_d z1,⋯,zd;
2.和上面的步骤2一样,将 z z z的第一部分 z 1 , ⋯ , z d z_1,\cdots,z_d z1,⋯,zd分别丢进两个网络 F F F和 H H H,分别得到 β d + 1 , ⋯ , β D \beta_{d+1},\cdots,\beta_D βd+1,⋯,βD和 γ d + 1 , ⋯ , γ D \gamma_{d+1},\cdots,\gamma_D γd+1,⋯,γD;
3.根据以下公式计算 z i > d z_{i>d} zi>d:
z i > d = x i − γ i β i z_{i>d}=\cfrac{x_i-\gamma_i}{\beta_i} zi>d=βixi−γi
Coupling Layer Jacobian矩阵计算
先把上面的Coupling Layer 结构简化成下面的样子,注意颜色:
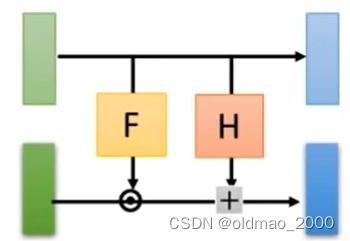
将Jacobian矩阵的计算结果分为四个部分,这里的颜色和上面的简化模型颜色是对应的:
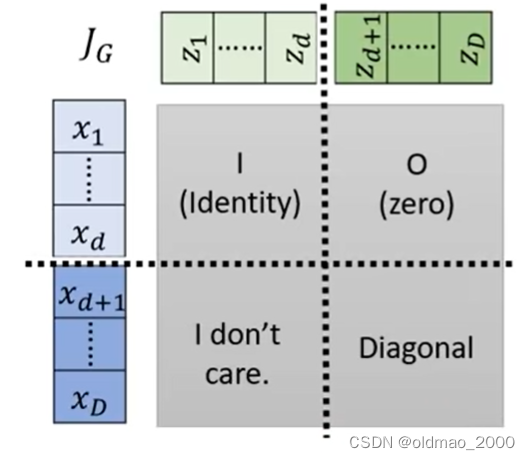
左上角是Identity矩阵,因为这里 x i < d = z i < d x_{i<d}=z_{i<d} xi<d=zi<d,浅蓝对浅绿的偏导结果除了对角线其他位置都是0;
右上角结果是0,因为这里浅蓝部分 x 1 , ⋯ , x d x_1,\cdots,x_d x1,⋯,xd与深绿部分 z d + 1 , ⋯ , z D z_{d+1},\cdots,z_D zd+1,⋯,zD无关,求偏导后均为0;
左下角的内容不需要考虑,因为左上角是Identity矩阵和右上角是0,整个灰色大矩阵的行列式的值等于右下角的行列式的值,这个是行列式的某个推论;
右下角就是要看深绿和深蓝部分的关系,他们的关系在上面有写:
x i > d = β i z i + γ i (8) x_{i>d}=\beta_iz_i+\gamma_i\tag8 xi>d=βizi+γi(8)
从这个式子可以看到, x d + 1 x_{d+1} xd+1只与 z d + 1 z_{d+1} zd+1有关,与 z d + 2 , ⋯ , z D z_{d+2},\cdots,z_D zd+2,⋯,zD无关,因此,右下角只有对角线上有值(但不为1),是一个对角线矩阵。
现在问题变成要求右下角矩阵行列式的值,由于右下角是一个对角线矩阵,因此其行列式的值等于对角线上的所有值的乘积(行列式定义简单推导即可得到该结论),可写为:
d e t ( J G ) = ∂ x d + 1 ∂ z d + 1 ∂ x d + 2 ∂ z d + 2 ⋯ ∂ x D ∂ z D det(J_G)=\cfrac{\partial x_{d+1}}{\partial z_{d+1}}\cfrac{\partial x_{d+2}}{\partial z_{d+2}}\cdots\cfrac{\partial x_D}{\partial z_D} det(JG)=∂zd+1∂xd+1∂zd+2∂xd+2⋯∂zD∂xD
根据公式8可以将每一项偏导求出来:
d e t ( J G ) = β d + 1 β d + 2 ⋯ β D det(J_G)=\beta_{d+1}\beta_{d+2}\cdots\beta_D det(JG)=βd+1βd+2⋯βD
Coupling Layer Stacking
下面来看Coupling Layer如何叠加,假设有多个Coupling Layer如下图
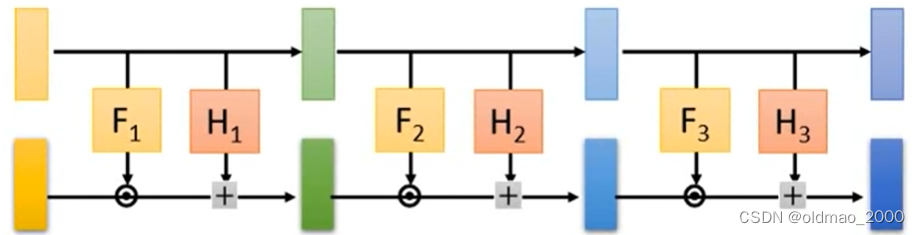
按照单个Coupling Layer的原理,我们发现它会把第一层浅黄色部分直接copy到最后一层,这样会使得最后的部分和原始输入的noise一样(原始输入是从搞屎分布中随机sample出来),这样没有啥意义。
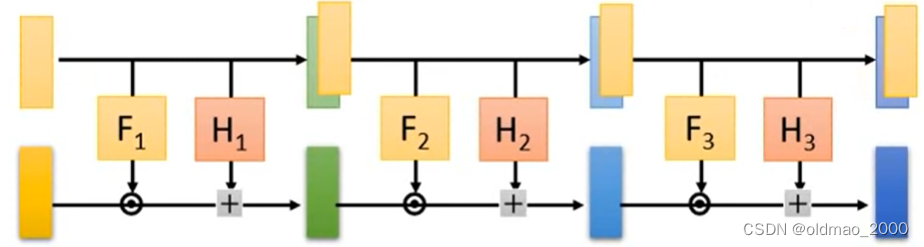
因此在堆叠的时候可以适当做一些反向,注意看函数的箭头:
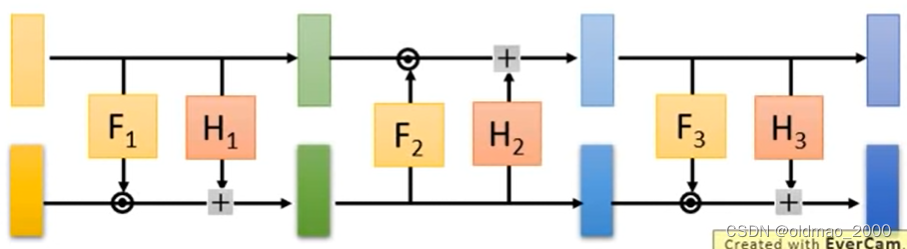
经过Copy操作后变成:
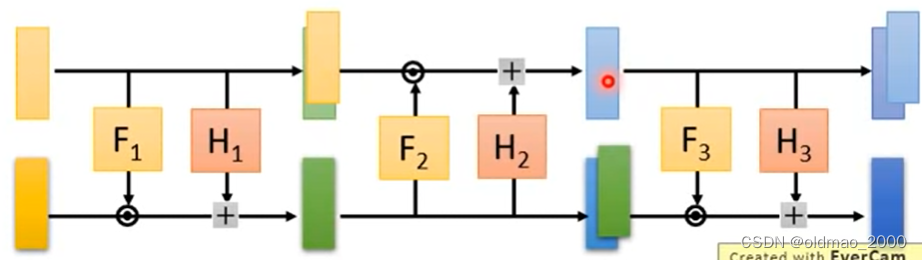
在做图像生成实操的时候如何做反向?有两种方法:
第一种,按棋盘式的前后两两反向

第二种,将图片的channel进行反接,一层做copy,一层做Transform:

两种方法还可以混合使用。
1×1 Convolution
另外一个技巧让基于Flow的网络构架对称的技巧就是1×1的卷积,这个是15年就提出来的概念,但是22年又用在了GLOW上面,使得我们在不使用GAN的情况下也能做图像生成。
Glow: Generative Flow with Invertible 1x1 Convolutions
假设输入为 z z z,输出为 x x x,由于是图像问题,图片中每个像素看做一个单位,且有RGB三个channel,1×1的卷积过程如下图所示:
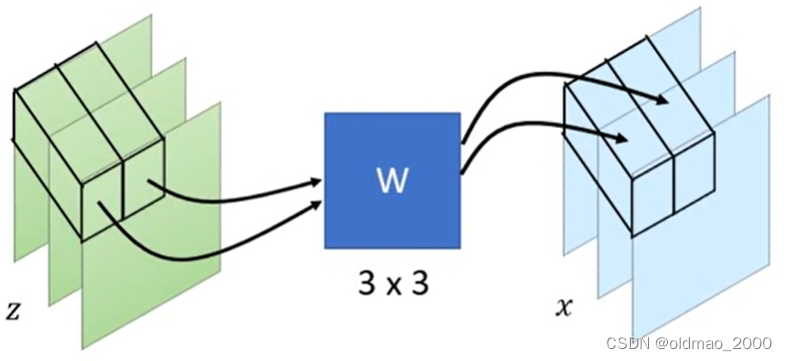
将 z z z中的每一个像素对应的3个channel与大小为3×3的矩阵 W W W相乘,得到x相同位置上的一个像素的3个channel。
x = f ( z ) = W z (9) x=f(z)=Wz\tag9 x=f(z)=Wz(9)
矩阵 W W W是通过训练学习得来,其作用为将3个channel进行shuffle,例如:
[ 0 0 1 1 0 0 0 1 0 ] W [ 1 2 3 ] = [ 3 1 2 ] \overset{W}{\begin{bmatrix} 0& 0&1 \\ 1 & 0&0 \\ 0 & 1 &0 \end{bmatrix}}\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}=\begin{bmatrix} 3 \\ 1 \\ 2 \end{bmatrix} 010001100 W 123 = 312
这样就可以使得在用Coupling Layer stacking的时候,不需要进行反接,而是让模型自己学习 W W W,决定如何来交换channel的位置。将 W W W加入Generator构架 G G G中后,也必须是是invertiable的,即: W W W必须存在 W − 1 W^{-1} W−1。GLOW文章中没有证明 W W W一定可逆,仅提到使用了存在 W − 1 W^{-1} W−1的 W W W进行初始化,并希望在模型自动学习收敛后, W W W还是可逆。当然三阶矩阵不可逆的条件比较苛刻(除非该矩阵对应的行列式值为0),一般三阶矩阵都可以满足可逆这一条件。
下面根据公式9来求单个像素点对应的Jacobian Matrix,将该公式写开:
[ x 1 x 2 x 3 ] = [ w 11 w 12 w 13 w 21 w 22 w 23 w 31 w 32 w 33 ] [ z 1 z 2 z 3 ] \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} &w_{23} \\ w_{31} &w_{32} &w_{33} \end{bmatrix}\begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix} x1x2x3 = w11w21w31w12w22w32w13w23w33 z1z2z3
Jacobian Matrix计算结果就为:
j f = [ ∂ x 1 / ∂ z 1 ∂ x 1 / ∂ z 2 ∂ x 1 / ∂ z 3 ∂ x 2 / ∂ z 1 ∂ x 2 / ∂ z 2 ∂ x 2 / ∂ z 3 ∂ x 3 / ∂ z 1 ∂ x 3 / ∂ z 2 ∂ x 3 / ∂ z 3 ] = [ w 11 w 12 w 13 w 21 w 22 w 23 w 31 w 32 w 33 ] = W j_f=\begin{bmatrix} \partial x_1/\partial z_1 & \partial x_1/\partial z_2 & \partial x_1/\partial z_3 \\ \partial x_2/\partial z_1 & \partial x_2/\partial z_2 & \partial x_2/\partial z_3 \\ \partial x_3/\partial z_1 & \partial x_3/\partial z_2 & \partial x_3/\partial z_3 \end{bmatrix}=\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} &w_{23} \\ w_{31} &w_{32} &w_{33} \end{bmatrix}=W jf= ∂x1/∂z1∂x2/∂z1∂x3/∂z1∂x1/∂z2∂x2/∂z2∂x3/∂z2∂x1/∂z3∂x2/∂z3∂x3/∂z3 = w11w21w31w12w22w32w13w23w33 =W
接下来看整个图片的Jacobian Matrix,假设图片大小是 d × d d\times d d×d:
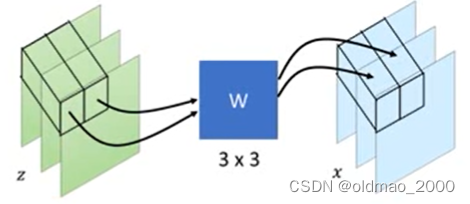
根据上面的图来看,只有对应位置上的像素点做了乘 W W W的操作,而与其他像素点是没有关系的,因而整个图片的Jacobian Matrix可以表示为下图:
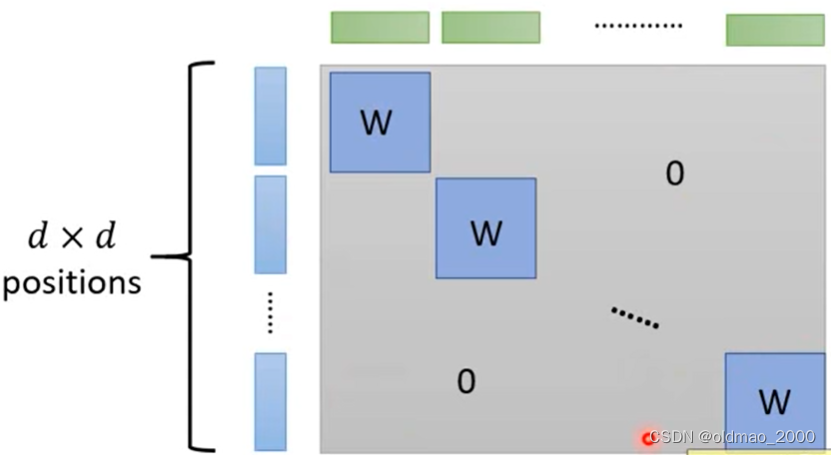
只有对角线部分是由一个个 W W W组成,其他位置都是0,根据线性代数的推论,整个矩阵的行列式的值为:
( d e t ( W ) ) d × d \left(det(W)\right)^{d\times d} (det(W))d×d
由于 W W W是3×3的矩阵,其行列式的值很容易算(可参加上面有公式)。
GLOW效果
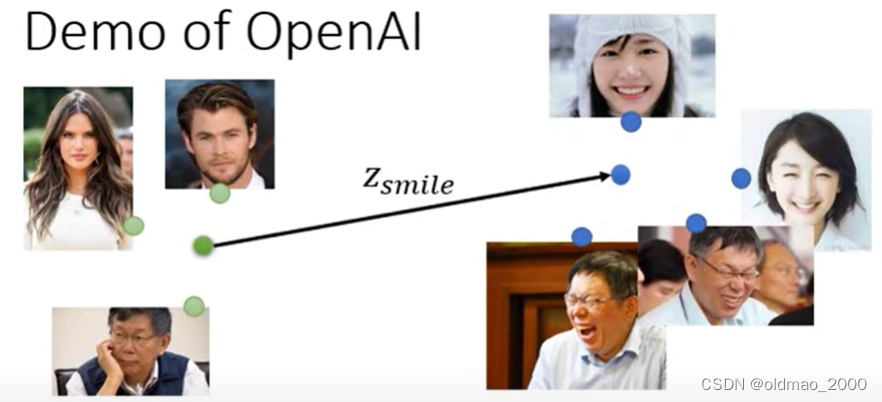
接下来演示了OpenAI的GLOW模型效果GLOW模型效果,合成:
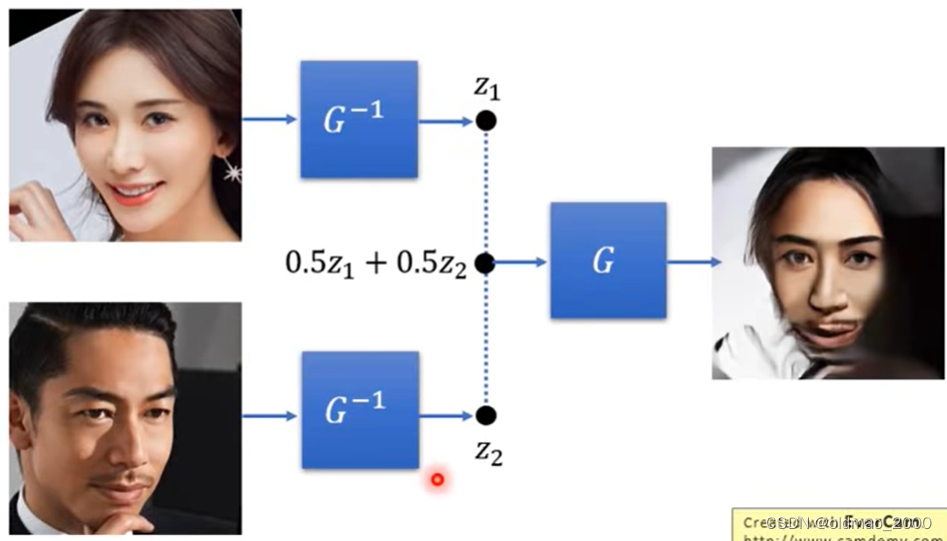
魔改笑脸,收集不笑的人脸和有笑容的人脸,通过 G − 1 G^{-1} G−1求向量后,分别求两组人脸的平均,然后求差就得到从不笑到笑之间的向量为 z s i m l e z_{simle} zsimle:
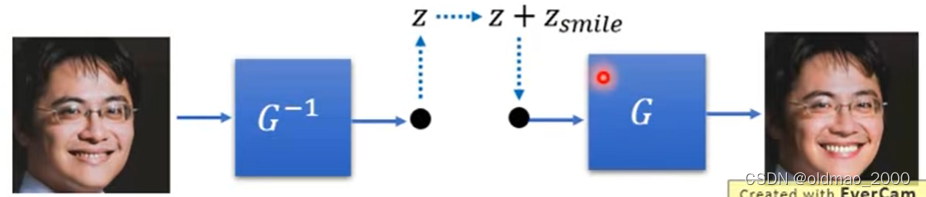
找一张要改笑容的图片,通过 G − 1 G^{-1} G−1求向量后,加上 z s i m l e z_{simle} zsimle,再过 G G G得到结果:
其他工作
语音合成
Parallel WaveNet: Fast High-Fidelity Speech Synthesis
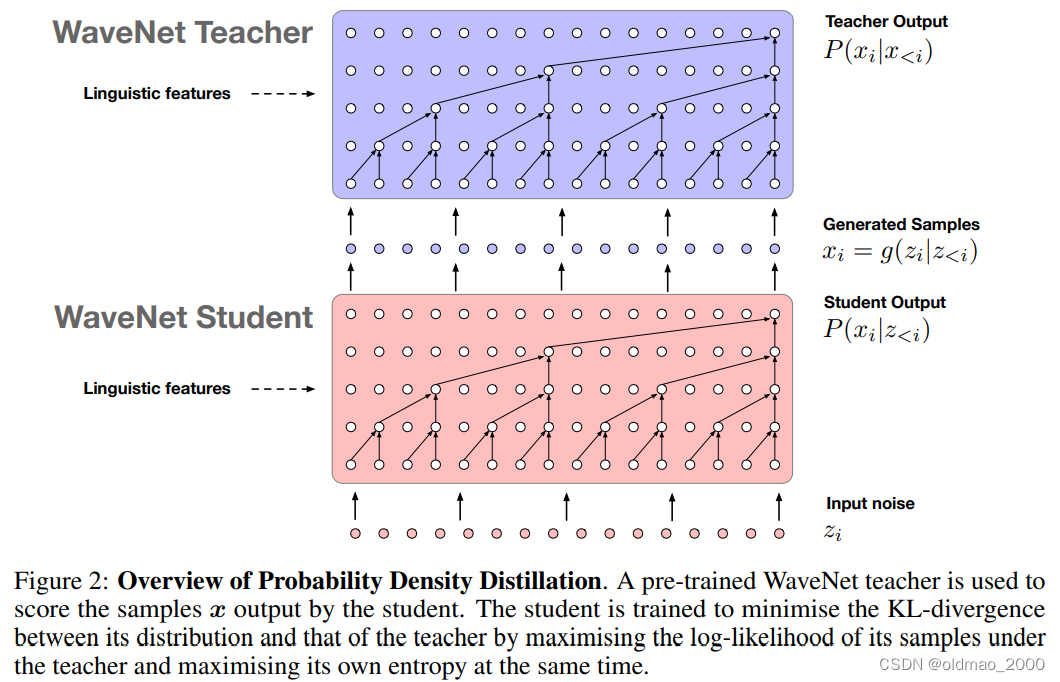
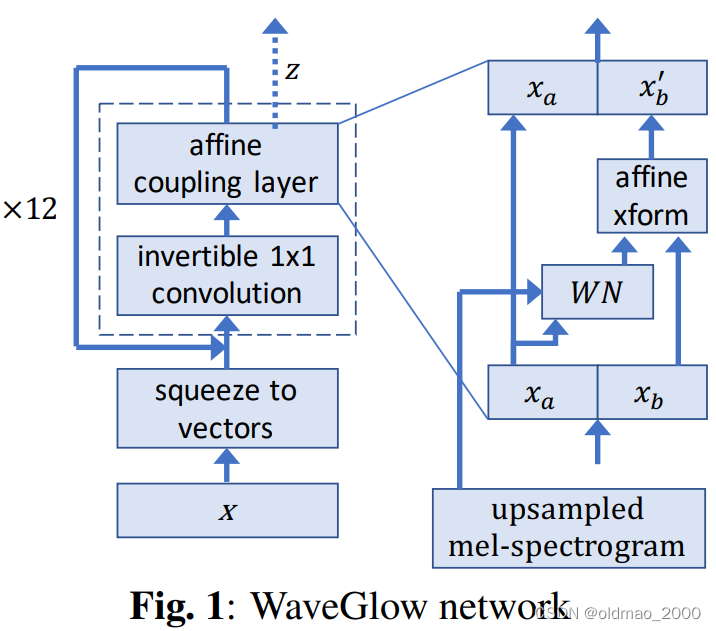
WaveGlow: A Flow-based Generative Network for Speech Synthesis