红黑树——插入底层实现【C++】面试重灾区！！

前言

一，概念

定义

二，insert

情况一：仅染色

情况二：单旋 + 染色

情况三：双旋 + 染色

insert代码

三，红黑树验证(面试题)

产生随机数验证

四，删除

下期预告：用红黑树封装map与 set

结语

每日一图区：

前言

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即$log_2 (N)$。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。

因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

红黑树相对于AVL树的优势包括：

插入和删除操作更快：红黑树相对于AVL树的平衡条件更加宽松，因此在插入和删除节点时需要进行的旋转操作更少。这使得红黑树的插入和删除操作更快。
更好的平衡性能：红黑树的平衡性能比AVL树稍差，但是在实际应用中，红黑树的平衡性能已经足够好了。红黑树的插入和删除操作相对较快，这在某些场景下更重要。
更少的旋转操作：红黑树的旋转操作比AVL树少。旋转操作是一种比较耗时的操作，因此红黑树的插入和删除操作相对更快。
更好的空间效率：红黑树相对于AVL树需要更少的额外空间来存储平衡因子或颜色信息。这使得红黑树的空间效率更高。
更广泛的应用：红黑树相对于AVL树应用更广泛。红黑树在很多语言的标准库中都有实现，而AVL树的应用相对较少。

需要注意的是，红黑树和AVL树都是平衡二叉搜索树，选择使用哪种树结构取决于具体的应用场景和需求。

一，概念

红黑树，是一种 二叉搜索树，但 在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。通过对 任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是 接近平衡的。

红黑树的性质：

1. 每个结点不是红色就是黑色

2. 根节点是黑色的

3. 如果一个节点是红色的，则它的两个孩子结点是黑色的

4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

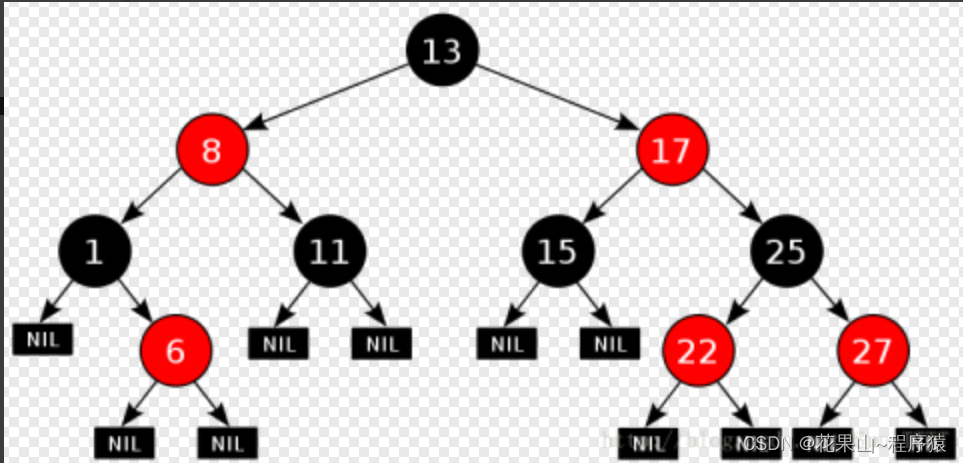
其中，NIL表示一个路径的出口。

定义

enum color{RED, BLACK};template <class data_type>
struct RBT_Data
{data_type _kv;RBT_Data<data_type>* left = nullptr;RBT_Data<data_type>* right = nullptr;RBT_Data<data_type>* parent = nullptr;color _col;  // 颜色RBT_Data(const data_type& p):_kv(p),_col(RED) // 颜色默认红{}
};template <class data_type>
class RB_Tree
{typedef RBT_Data<data_type> RBT_Data;RBT_Data* root;
};

关于，创建新节点该怎么选颜色。

如果我们选择黑色，那么我们一定会违反性质四（对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点 ），我们为了保持红黑树的结构，就需要调整其他所有的路径。
如果我们选择红色，我们可能会违法性质三（如果一个节点是红色的，则它的两个孩子结点是黑色的 ），而且影响的只是局部，不会影响其他的兄弟树。

因此我们会选择红色作为默认颜色。

在AVL树中我们关注树之间的高度，而到了红黑树我们需要关注节点之间的颜色。

二，insert

插入新节点，我们需要检测新节点是否破坏红黑树的性质。

因为 新节点的默认颜色是红色，因此：如果 其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不需要调整；

但 当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连在一起的红色节点，此时需要对红黑树分情况来讨论：

情况一：仅染色

特点：uncle存在且为红，parent为红色，cur也为红

用一个模板图总结该情况：

情况二：单旋 + 染色

特征：没有uncle, parent为红, cur为红

所以在情况二下，比较重要的就是旋转方法+变色，旋转如果有忘记了，可以参考本篇文章：

保姆级认识AVL树【C++】（精讲：AVL Insert）-CSDN博客

情况三：双旋 + 染色

特征：没有uncle或者uncle是黑色，parent为红，cur为红。相比较于情况二，情况三的旋转方法是双旋。

这里有一个区分情况二与情况三的小技巧，那就是看grandfather , parent, cur 三节点的线路。如果是直线，则情况二；折线则情况三。

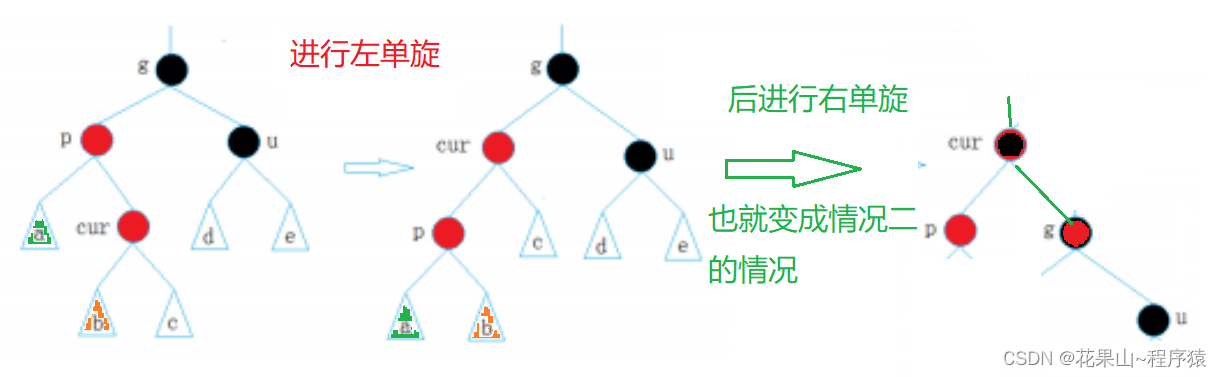
insert代码

bool insert(const pair<K, V>& p){RBT_Data* new_a_d = new RBT_Data(p);if (!root){root = new_a_d;root->_col = BLACK;	}else{RBT_Data* cur = root;RBT_Data* parent = nullptr;while (cur){if (p.first < cur->_kv.first){parent = cur;cur = cur->left;}else if (p.first > cur->_kv.first){parent = cur;cur = cur->right;}else{delete(new_a_d); // 插入失败，删除新建结点return false;}}if (p.first < parent->_kv.first){parent->left = new_a_d;}else{parent->right = new_a_d;}new_a_d->parent = parent;// 调整颜色cur = new_a_d;RBT_Data* par = cur->parent;if (cur == root){cur->_col = BLACK;}while (par && par->_col == RED){RBT_Data* gf = par->parent;RBT_Data* uncle = nullptr;if (gf && par == gf->right){uncle = gf->left;}else if (gf && par == gf->left){uncle = gf->right;}else{assert(false);}if ( uncle && uncle->_col == RED)// 有u且为红{gf->_col = RED;uncle->_col = BLACK;par->_col = BLACK;cur = gf;  // 切换为祖先，进入循环向上par = cur->parent;}else if (!uncle ||(uncle && uncle->_col == BLACK)){   // 情况2 + 3，判断，是否是折线还是直线if (gf->left == par && par->left == cur){  // 右单选RotateR(gf);}else if (gf->right == par && par->right == cur){  // 左单旋RotateL(gf);}else if (gf->left == par && par->right == cur){  // 需要左双旋RotateLR(gf);}else if (gf->right == par && par->left == cur){  // 需要右双旋RotateRL(gf);}else{assert(false);}break;}else{assert(false);}}if ( root->_col == RED){root->_col = BLACK;}return true;}
}

左，右和双旋实现代码跟AVL章节中大差不差，这里给出左单旋的实现，大家照葫芦画瓢一下：

void RotateL(RBT_Data* parent){assert(parent->right);RBT_Data* par = parent;RBT_Data* par_R = par->right;RBT_Data* par_RL = par->right->left;RBT_Data* ppnode = par->parent;par->right = par_RL;if (par_RL)par_RL->parent = par;par_R->left = par;par->parent = par_R;par_R->parent = ppnode;if (!ppnode){root = par_R;}else if (ppnode->left == par){ppnode->left = par_R;}else{ppnode->right = par_R;}par->_col = RED;par_R->_col = BLACK;}

三，红黑树验证(面试题)

验证红黑树性质

目标：

1. 根是否是黑

2. 没有连续红节点

3. 每条路径所经历的黑节点相同。

代码：

public:
bool IsBalance(){if (root && root->_col == RED){return false;}int BlackNum = 0; // 所经黑节点的次数int standard = 0;  //设置一个最长路径RBT_Data* cur = root;while (cur){if (cur->_col == BLACK)standard++;cur = cur->left;}return _IsBalance(root->left, BlackNum, standard) && _IsBalance(root->right, BlackNum, standard);}private:
bool _IsBalance(const RBT_Data* cur, int BlackNum, int standard){if (cur == nullptr){return true;}if (cur->_col == BLACK)BlackNum++;if (cur->_col == RED && cur->_col == cur->parent->_col){return false;}return  _IsBalance(cur->left, BlackNum, standard) && _IsBalance(cur->right, BlackNum, standard);}

产生随机数验证

void Random_Test()
{srand(time(0));const size_t N = 10000000;RB_Tree<int, int> t;for (size_t i = 0; i < N; i++){size_t x = rand();t.insert(make_pair(x, x));}cout << t.IsBalance() << endl;
}