本篇博客介绍: 简单介绍下贪心算法
贪心算法
- 介绍贪心算法
- 最小字典序的字符串拼接
- 最多会议数
- 切棍子的最小成本
- IPO
- 灯塔问题
介绍贪心算法
贪心算法是一种极具有自然智慧的算法
它会使用以一种局部最功利的标准来做出一个当前看来最好的选择
如果说我们根据局部最优解算出了全局最优解 那么这就是一个有效的贪心
反之我们就可以说 这是一个无效的贪心
(也就是说 我们用贪心算法做题是可能出错的!)
贪心算法的难点在于 我们如何使用局部最功利的标准去得到全局最优解
所以说贪心算法并没有一套很固定的模板 对于贪心算法的学习我们只能是增加阅历和经验为主
下面是贪心算法的反例
现在A要从起点走到终点 再从终点走到起点 从起点到终点的过程中只能够向下或者向左 从终点到起点的过程中智能向上或者向右
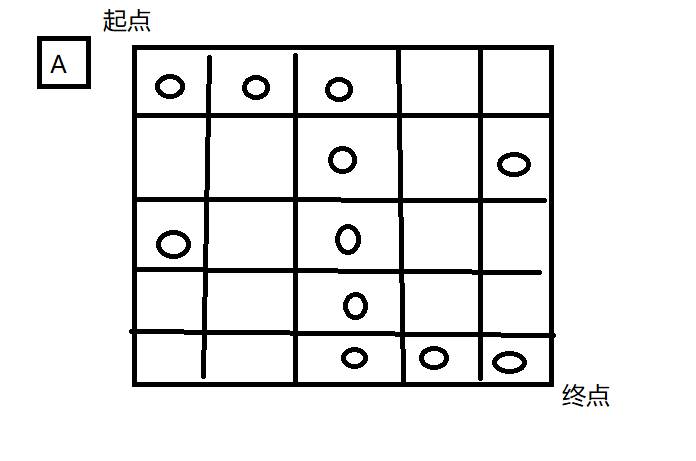
如果我们根据贪心算法来解决 我们的思路是
- 去的时候尽量拿到更多的节点
- 回来的时候尽量拿到更多的节点
我们的路线应该是这样子的

我们可以发现我们少拿了一个节点
但是最佳的路线其实应该是这样子
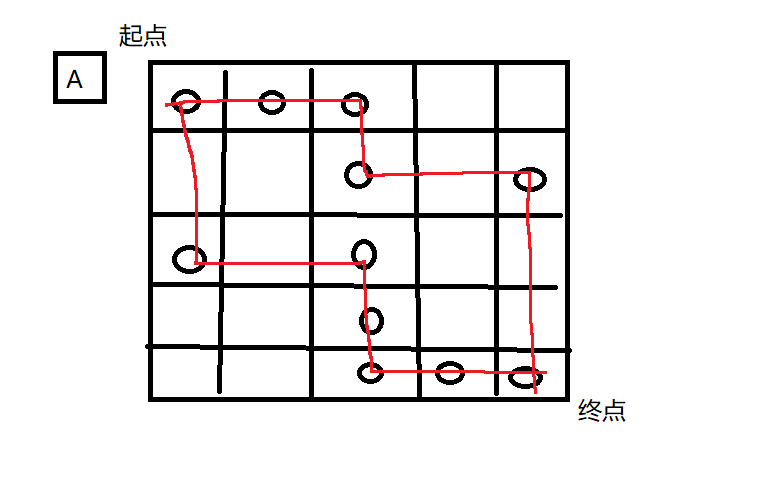
我们全部的节点都拿到了
上面的例子只是为了证明 贪心算法也会出错
最小字典序的字符串拼接
题目如下:
给定我们一个由字符串拼接而成的数组strs 我们必须要把所有的字符串拼接出来 要求我们返回一个字典序最小的拼接结果
首先我们能够确定的是 我们最后拼接出来的字符串长度肯定是一样的
这里同学们一般的贪心策略可能是我们将字符串按照字典序排个序 然后直接拼接起来即可
虽然大部分情况下这种策略是对的 但是也有反例
比如说两个字符串 “b” “ba”
我们明显可以看出 拼接出的最小字符串应该是bab
可以如果按照我们的算法 我们得到的就是字符串bba 明显不对
正确的贪心算法如下
我们按照以下结果排序 如果a拼接上b 小于 b拼接上a 则a在前 反之b在前
使用我们正确的贪心算法就能够得到正确的结果 "bab"了
关于上面贪心的证明过程有点复杂 而且就算知道了如何证明也没有什么意义 其他的题目并不通用 这也就是为什么说学习贪心算法只是为了增加阅历
如果对于这个证明过程有兴趣的同学可以去b站查看左神的算法课学习
这道题我们可以在牛客网上做
最小字典序
代码表示如下
#include <iostream>
using namespace std;
#include <string>
#include <vector>
#include <algorithm>bool Less(const string& s1 , const string& s2){return s1 + s2 < s2 + s1;}int main()
{int count = 0;cin >> count;vector<string> strs;strs.resize(count);int i = 0;string str;while (count--){cin >> str;strs[i] = str;i++;}sort(strs.begin() , strs.end() , Less);string ans;for (int j = 0; j < strs.size() ; j ++){ans += strs[j];}cout << ans << endl;
}
还有就是 一般来说面试的时候不会考查贪心算法
如果考查了 那么我们可以直接跟面试官说 我不确定我的思路对不对 但是我可以使用对数器 一个个来验证我的思路
最多会议数
给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。
你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。
请你返回你可以参加的 最大 会议数目。
这道题我们贪心的想法可能会有很多 比如说:
- 我们每次排序之后选出时间最早的会议 之后继续排序
- 我们每次选择间隔时间短的会议
- 我们每次都选择结束时间最早的
显然 我们能够提出很多种贪心的方法 但是我们没有办法去一一证明 最快的方式就是直接写出一个暴力方式 然后将上面的几种方案全部写成代码 使用对数器一一对应
对数器能过 那就大概率是对的
我们这里直接给出结论 我们要选择每次开始时间最早的会议
因为我们要尽可能多的参加会议 所以说我们每天的时间最好都是能够用起来的
所以说 我尽量使用date日期来遍历
当然 题目中的隐藏条件就是可以使用的日期等于会议的最后一天 所以说我们也可以利用上这个隐藏条件
我们的整体思路如下
- 首先将所有的会议 按照日期的开始进行排序
- 我们创造一个小根堆 用来存放目前可以被使用的会议
- 如果说当前的日期大于等于会议的开始日期 我们就将所有的会议开始日期进入堆中
- 如果堆中存在可以开的会议我们就开会 如果不存在我们就data++ 直到堆中有数据为止
代码表示如下
class Solution {
public:static bool Less(vector<int>& v1 , vector<int>& v2){return v1[0] < v2[0];}int maxEvents(vector<vector<int>>& events) {sort(events.begin() , events.end() , Less);priority_queue<int , vector<int> , greater<int>> pq;int date = 1;int count = 0;int pointer = 0; while (pq.size() || pointer < events.size()){while (pointer < events.size() && events[pointer][0] <= date){pq.push(events[pointer][1]);pointer++;}if (pq.size()){count++;pq.pop();while(pq.size() && pq.top() == date){pq.pop();}}date++;}return count;}
};
切棍子的最小成本
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
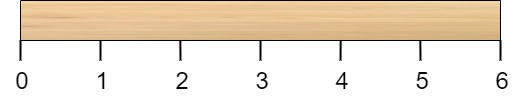
现在我们给定一个数组 数组格式如下 3 2 1 或者 2 2 2 2
总之 该数组的和一定为木棍的长度 现在告诉你 每次切割木棍要花费的代价为木棍的长度 要求怎么样切割花费的代价最小
这道题目的解题代码很简单 但是思路证明很难 还是一样 我们只给出代码思路 对于证明思路有兴趣的同学可以自己去研究
我们数组中所有的数加入到一个小根堆中 设置一个总代价sum
当小根堆的元素大于2的时候 我们每次取出两个元素相加 sum加上这两个元素后 将这两个元素相加后的值再次放进小根堆中
最后我们得到的结果sum就是答案了
IPO
假设 力扣(LeetCode)即将开始 IPO 。为了以更高的价格将股票卖给风险投资公司,力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限,它只能在 IPO 之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k 个不同项目后得到最大总资本的方式。
给你 n 个项目。对于每个项目 i ,它都有一个纯利润 profits[i] ,和启动该项目需要的最小资本 capital[i] 。
最初,你的资本为 w 。当你完成一个项目时,你将获得纯利润,且利润将被添加到你的总资本中。
总而言之,从给定项目中选择 最多 k 个不同项目的列表,以 最大化最终资本 ,并输出最终可获得的最多资本。
这个的贪心我相信大家能够很轻松的想出来 思路如下
- 我们首先找到我们能够参与的项目(需要资金小于等于我们的资金)
- 之后将这些项目按照利润排序 放到一个大堆中
- 之后我们做完一个项目之后更新我们的资金 之后找我们能够参与的项目
- 找到我们能够参与的项目之后 继续放入大堆中 重复上面的操作
这里有一个小细节是 如果我们的初始资金为0 并且没有可以做的项目的话 我们要直接return 0才行
代码表示如下
class Solution {
public:static bool less(const pair<int,int>& kv1 , const pair<int,int>& kv2){return kv1.first < kv2.first; }int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {vector<pair<int , int>> v;int sum = w;int count = k;int pointer = 0;// 将项目的资金排序for (int i = 0; i < profits.size() ; i++){v.push_back({capital[i] , profits[i]});}sort(v.begin() , v.end() , less);priority_queue<int> pq;while(count--){while(pointer < v.size()){if (v[pointer].first <= sum){pq.push(v[pointer].second);pointer++;}else {break;}}if (pq.empty()){return sum;}sum += pq.top();pq.pop();}return sum;}
};
灯塔问题
有一排灯塔,每个灯塔都有一盏灯,每盏灯可以照亮相邻的两个范围(左边一个和右边一个),但是不能跨过其他灯塔。现在给你一个由字符’X’和’.'组成的字符串,‘X’表示灯塔,’.'表示空地。请你计算最少需要打开多少盏灯,才能让所有的灯塔都被照亮
这也是一个典型的贪心问题
我们的解题思路如下
- 从头开始遍历整个字符串
- 如果遇到了空地 我们不管他
- 如果遇到了灯塔 我们查看灯塔后面的一个元素是什么
- 如果是空地 则我们开灯并且跳跃到空地后一个元素
- 如果是灯塔 那么我们开启后面一个灯塔 并且跳跃着开启灯塔后面的两个位置
代码也很简单 这里就不给出了
总结下 贪心算法并没有一个固定的套路 只能多做 你做过了你就会 你不做你就不会
证明的思路我们不必去一步步验证 对数器能过就说明我们的思路是正确的