503.下一个更大元素Ⅱ

• 力扣题目链接

• 代码随想录讲解链接

• 题意：给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

  数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

    示例 1:输入: nums = [1,2,1]输出: [2,-1,2]解释: 第一个 1 的下一个更大的数是 2；数字 2 找不到下一个更大的数； 第二个 1 的下一个最大的数需要循环搜索，结果也是 2。示例 2:输入: nums = [1,2,3,4,3]输出: [2,3,4,-1,4]
  

• 思路：和每日温度是一样的，把数组遍历两遍就行。

class Solution {public int[] nextGreaterElements(int[] nums) {int[] res = new int[nums.length]; //存放结果Arrays.fill(res, -1); //默认全部初始化为-1Deque<Integer> stack = new LinkedList<>(); //栈中存放的是nums中的元素下标stack.push(0);for(int i = 0; i < 2 * nums.length; i++) { //遍历两遍nums数组 while(!stack.isEmpty() && nums[i % nums.length] > nums[stack.peek()]) {//i对nums数组的长度取余，就可以遍历两遍取到相应的元素res[stack.peek()] = nums[i % nums.length];stack.pop();}stack.push(i % nums.length);}return res;}
}

42.接雨水

• 力扣题目链接

• 代码随想录讲解链接

• 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
  

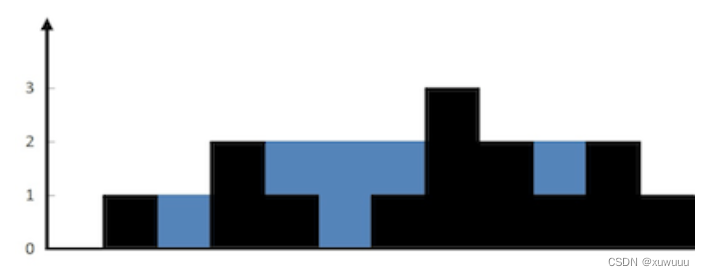
    示例 1：输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]输出：6解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。示例 2：输入：height = [4,2,0,3,2,5]输出：9
  

• 暴力解法
  按列计算，每一列所能接到的雨水，是此列左边最高的列和此列右边最高的列中较小的值决定的，那么此列能接到的雨水的高度就是min(右侧最高， 左侧最高) - 本身高度。

  时间复杂度O(n^2)

class Solution {public int trap(int[] height) {int sum = 0;for(int i = 0; i < height.length; i++) {if(i == 0 && i == height.length-1) continue;int rHeigth = height[i];int lHeight = height[i];for(int r = i+1; r < height.length; r++) {if(height[r] > rHeigth) rHeigth = height[r];}for(int l = i-1; l >= 0; l--) {if(height[l] > lHeight) lHeight = height[l];}int h = Math.min(rHeigth,lHeight) - height[i];if(h > 0) sum += h;}return sum;}
}

• 双指针优化
  暴力解法中，需要记录左右两边柱子的最高高度，为了得到两边的最高高度，可以使用双指针遍历。

  每到一个柱子都向两边遍历一遍，这样就会有重复计算。所以把每一个位置的左边最高高度记录在数组maxLeft上，右边最高高度记录在数组maxRight上。

  每到一个柱子，其左右两边的最高高度则是左右两边前一个位置的左右两边的最高高度和本位置的高度的最大值。在计算最高高度时把自己也算进去了

  maxLeft[i] = Math.max(maxLeft[i-1], heigth[i])；
  maxRight[i] = Math.max(maxRigth[i+1], heigth[i]);

class Solution {public int trap(int[] height) {int[] maxLeft = new int[height.length];int[] maxRight = new int[height.length];//第一个位置的左边最高高度是自己。maxLeft[0] = height[0];for(int i = 1; i < height.length; i++) {maxLeft[i] = Math.max(maxLeft[i-1], height[i]);}//最后一个位置的右边最高高度是自己。maxRight[height.length-1] = height[height.length-1];for(int i = height.length-2; i >= 0; i--) {maxRight[i] = Math.max(maxRight[i+1], height[i]);}int res = 0;for(int i = 0; i < height.length; i++) {int count = Math.min(maxLeft[i], maxRight[i]) - height[i];if(count > 0) res += count;} return res;}
}

• 单调栈