目录
1 Unet
1.1详细整体结构
1.2 缩小版整体结构
1.3 时间步编码
1.4 CrossAttnDownBlock2D
1.4.1 ResnetBlock2D
1.4.2 Transformer2DModel
1.4.2.1 BasicTransformerBlock
1.4.2.1.1 SelfAttention
1.4.2.1.2 CrossAttention
1.4.2.1.3 FeedForward
1.4.3 DownSample2D
1.5 DownBlock2D
1.6 UnetMidBlock2DCrossAttn
1.7 UpBlock2D
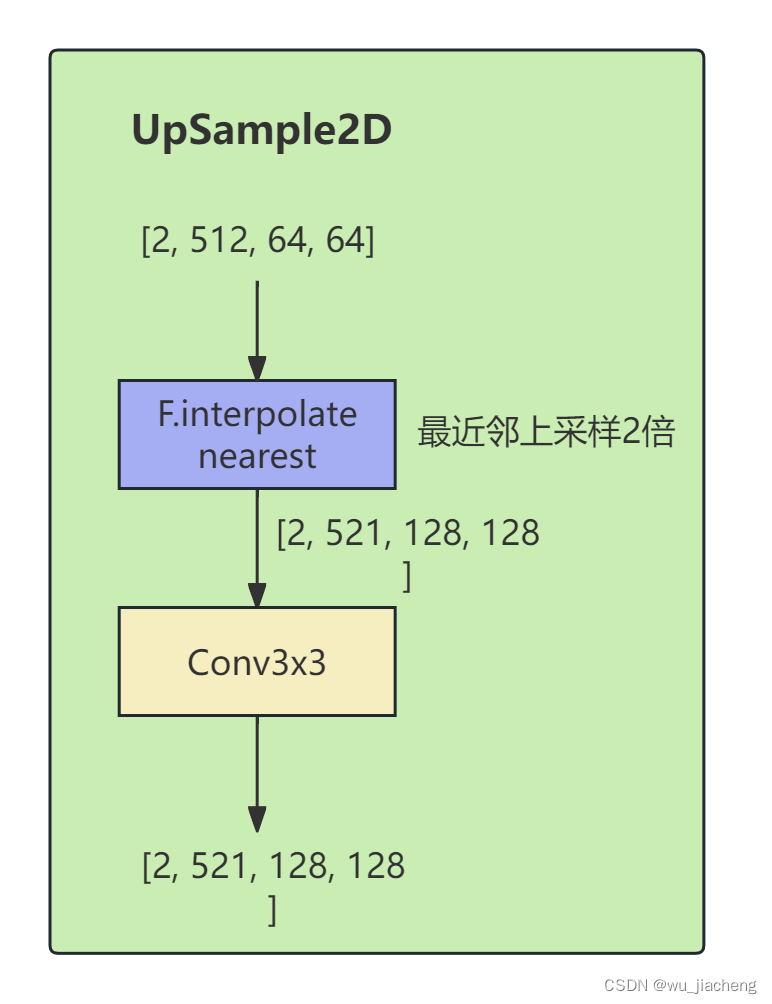
1.7.1 UpSample2D
1.8 CrossAttnUpBlock2D
2 VAE
3 CLIP
绘制软件:ProcessOn,以下图片保存可高清查看
1 Unet
1.0 介绍
负责预测噪声
1.1详细整体结构
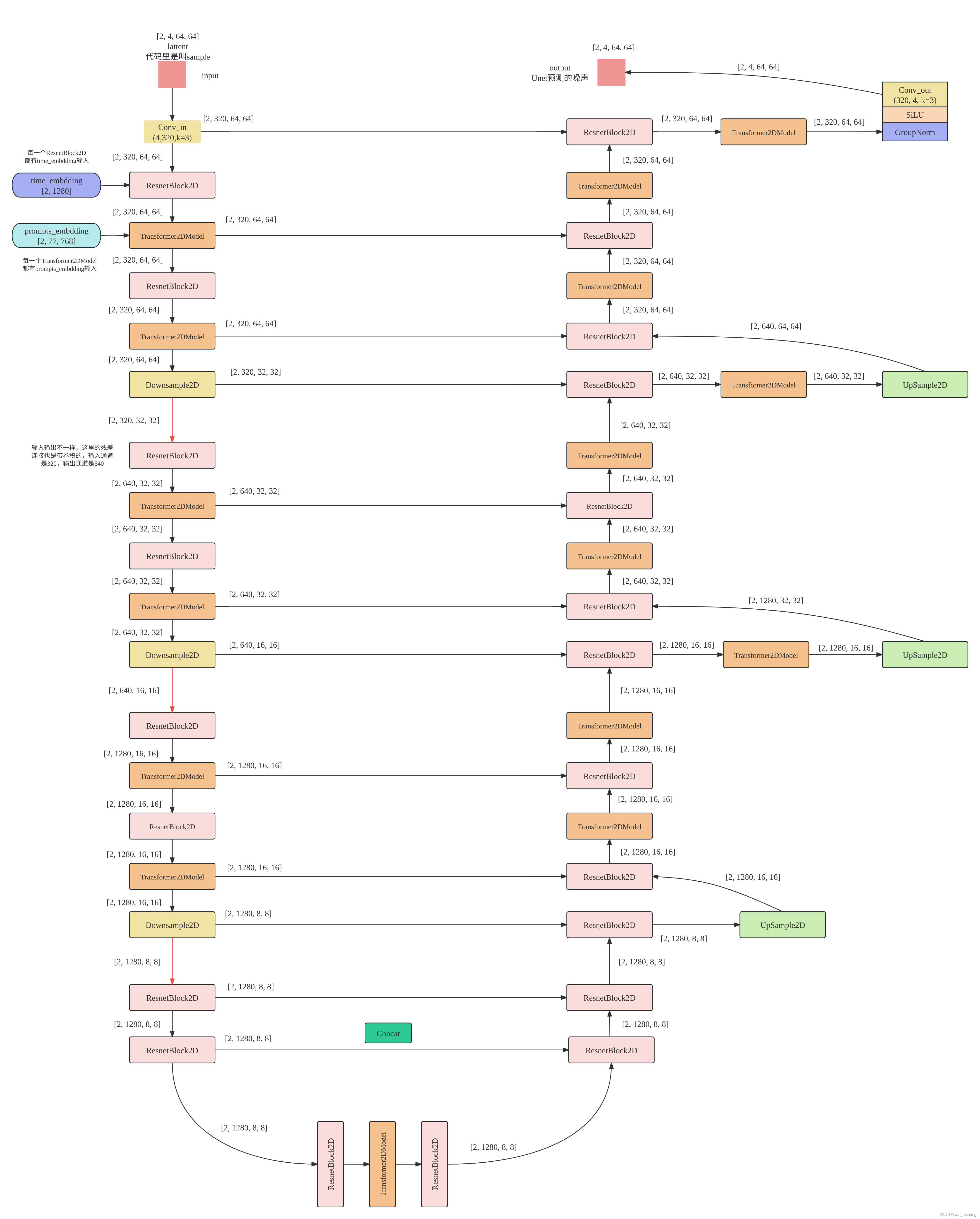
1.2 缩小版整体结构
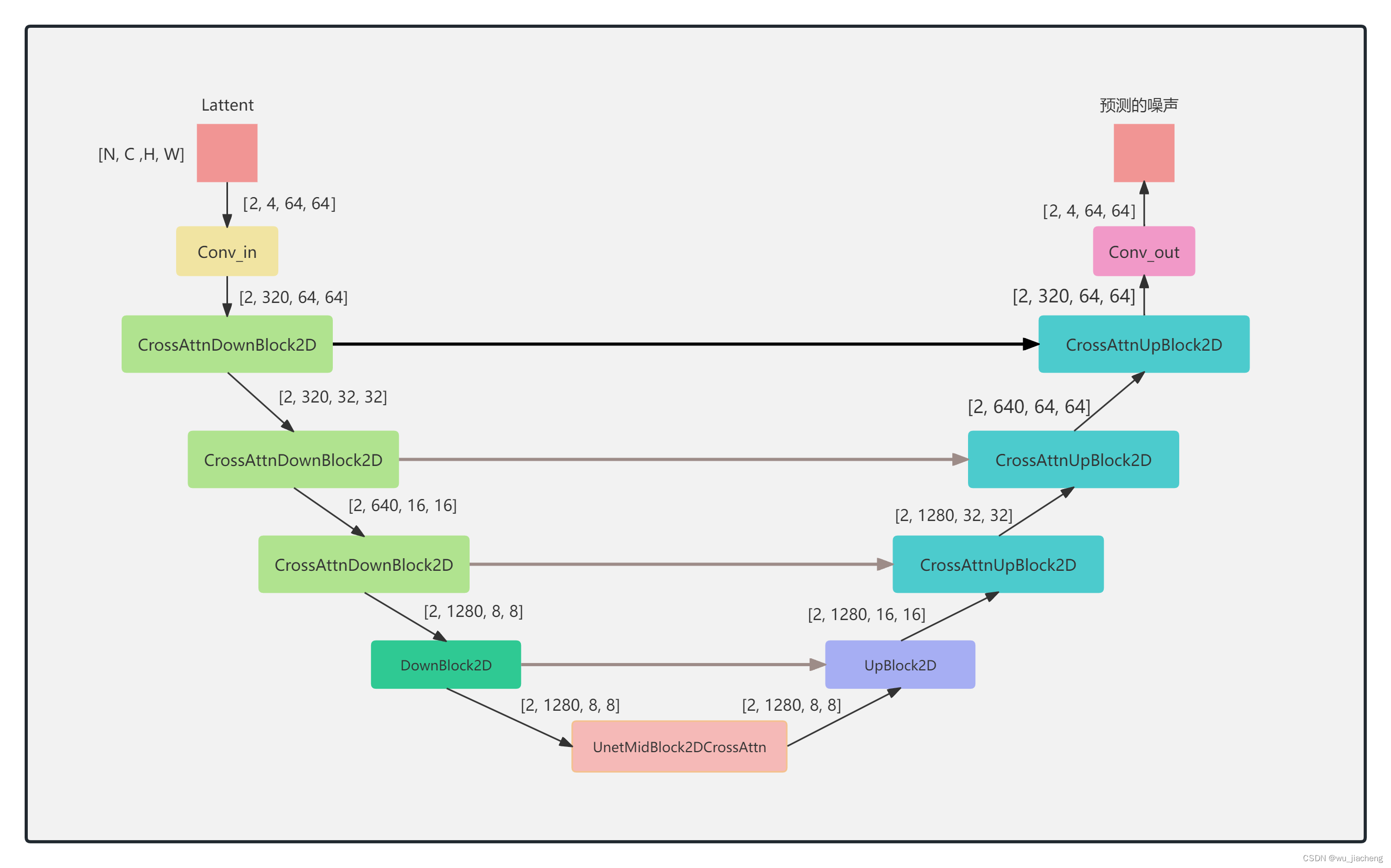
1.3 时间步编码
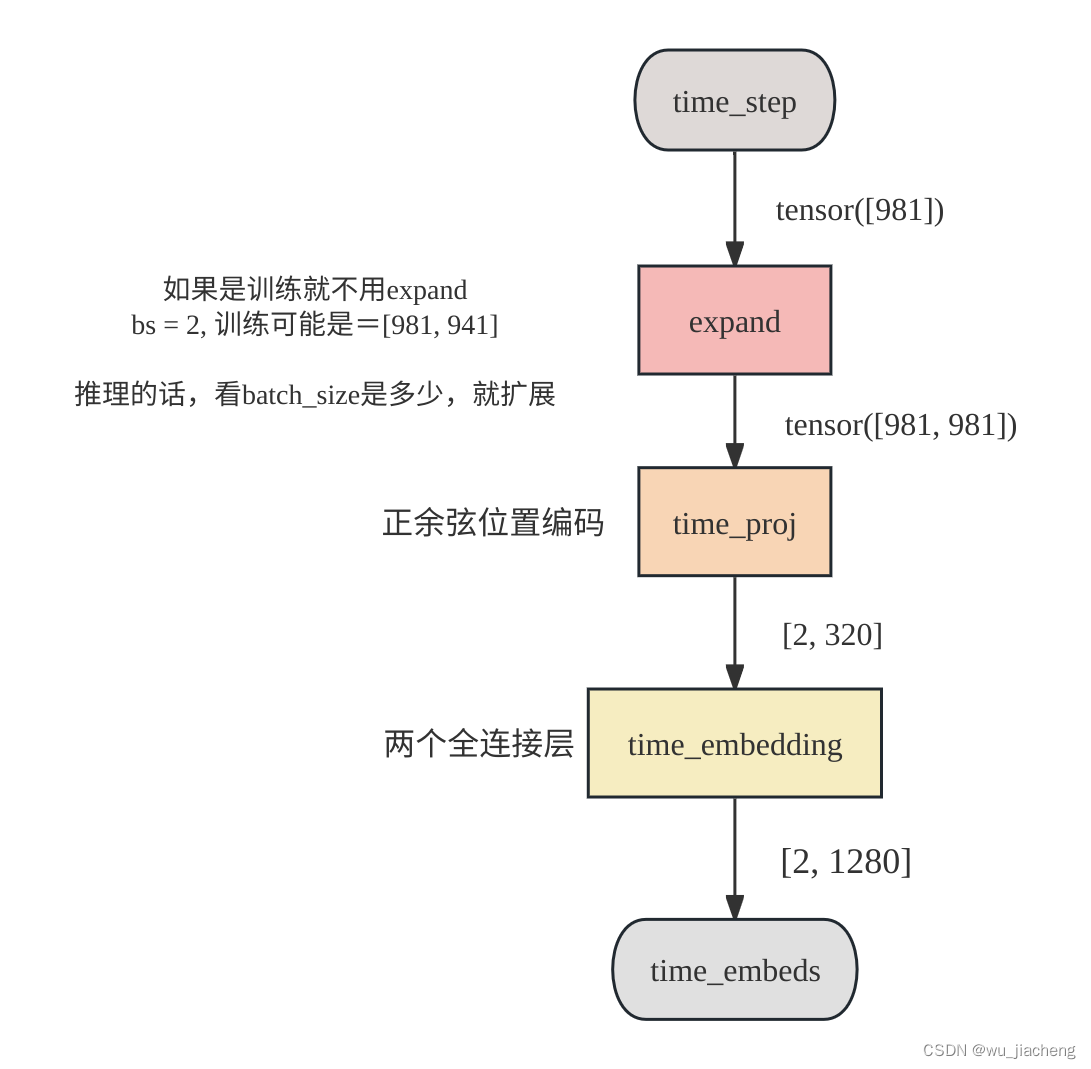
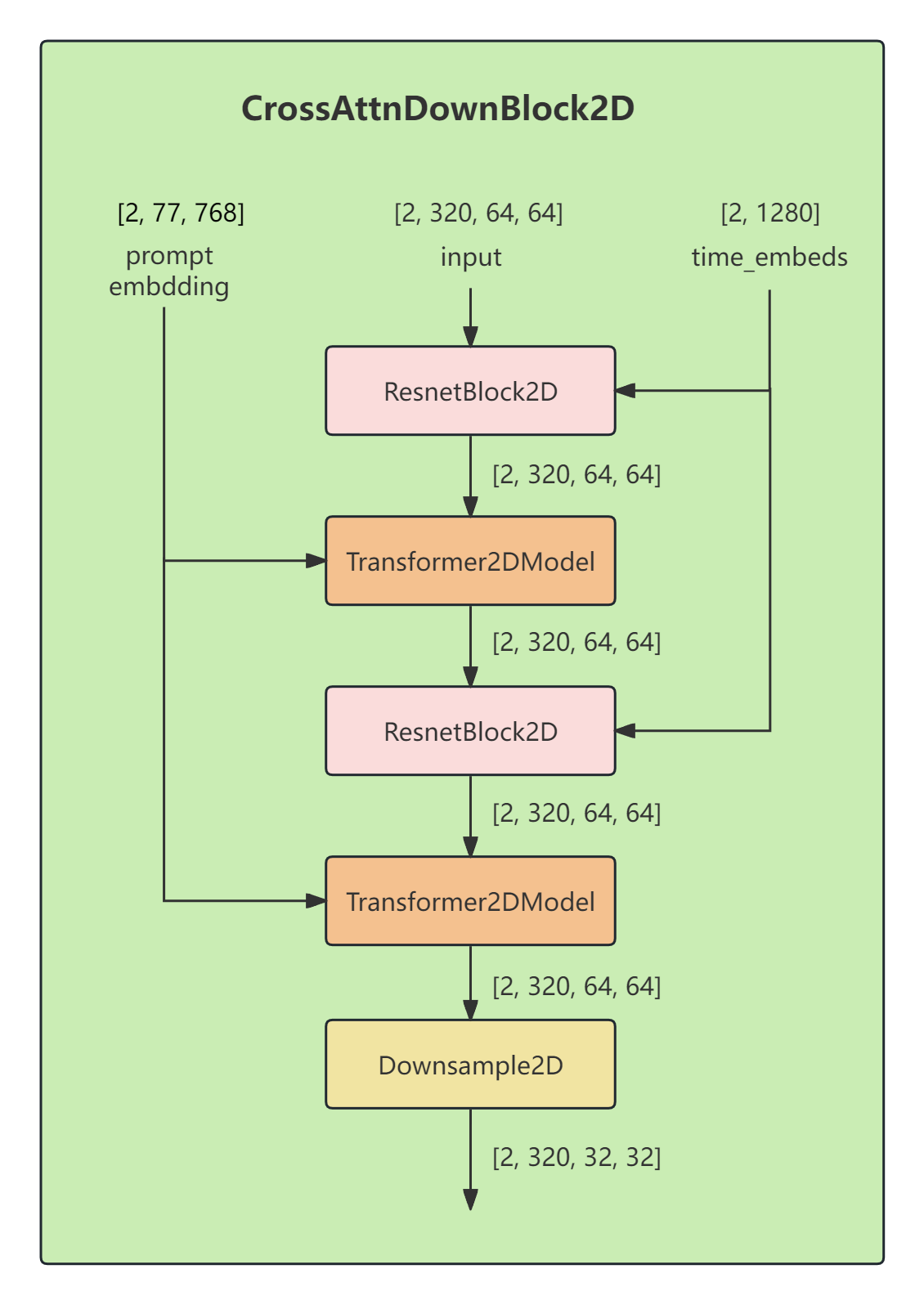
1.4 CrossAttnDownBlock2D
每个ResnetBlock2D的输入有两个
1,一个是来自上一层的输出lattent,
2,另一个来自时间步编码模块的输出time_embeds ( shape=[2, 1280], 后面省略说明,默认[2, 1280]这种写法是tersor的形状)
每个Transformer2DModel输入有两个
1,上一层的输出
2, CLIP text_encoder的文本编码text embedding,或者叫提示词编码prompt embedding,其shape=[2, 77, 768]
后面凡是有ResnetBlock2D和Transformer2DModel的模块,其输入形式都是如此,为了方便,后面有些模块的time_embeds和prompt embedding这两个输入就默认不画了,例如UnetMidBlock2DCrossAttn、UpBlock2D、CrossAttnUpBlock2D
1.4.1 ResnetBlock2D
需要注意的点
1, ResnetBlock2D的输入有两个,一个是来自上一层的lattent,另一个来自时间步编码模块的输出time_embeds ( shape=[2, 1280], 后面省略说明,默认[2, 1280]这种写法是tersor的形状)
2, Conv3x3和Linear的输入输出Channel,不同层会不一样
3, 输入输出通道数不一致的时候,残差连接会用一个1x1的卷积

1.4.2 Transformer2DModel
Transformer2DModel输入有两个
1,上一层的输入
2, CLIP text_encoder的文本编码text embedding,或者叫提示词编码prompt embedding,其shape=[2, 77, 768]
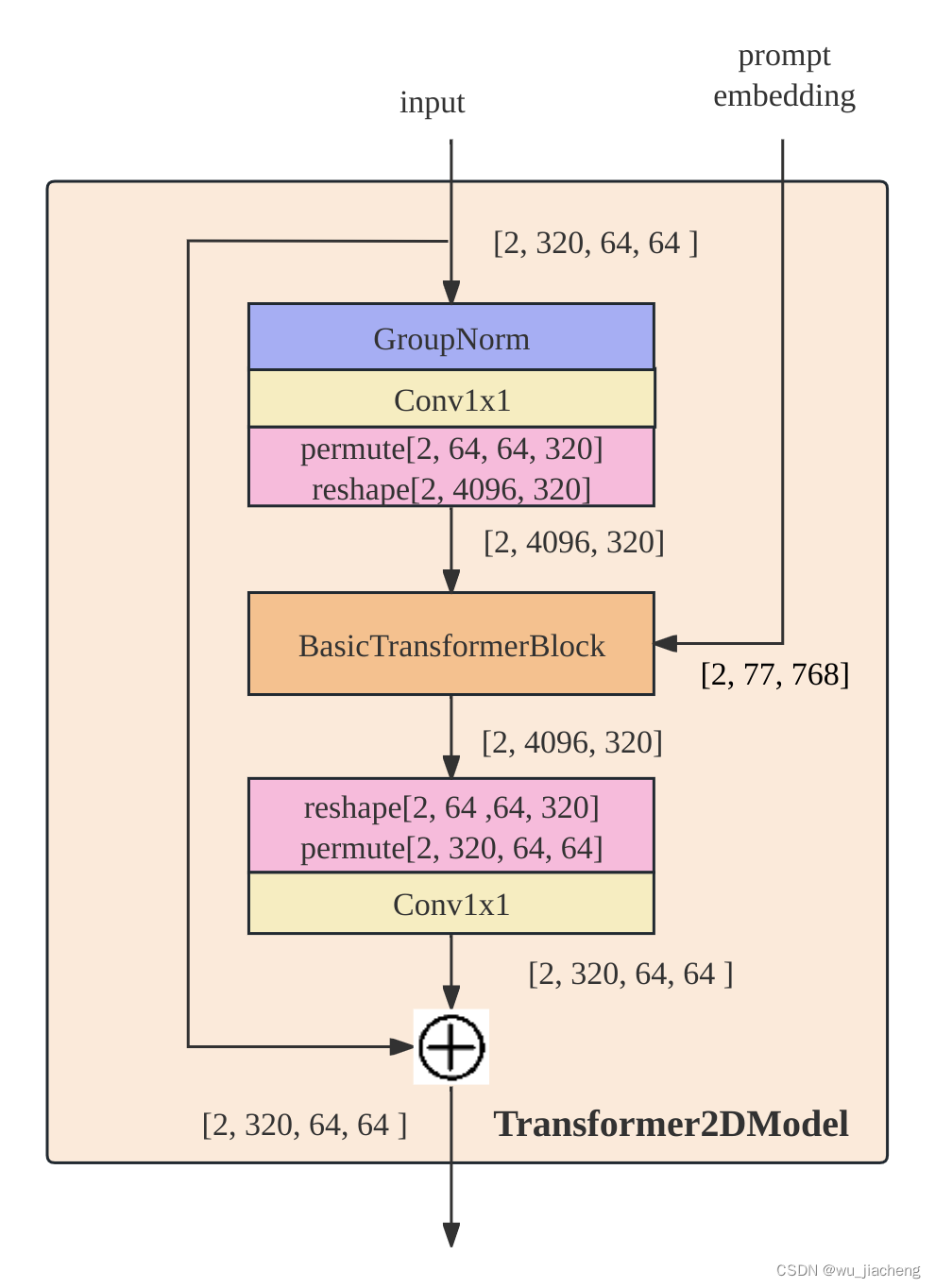
1.4.2.1 BasicTransformerBlock
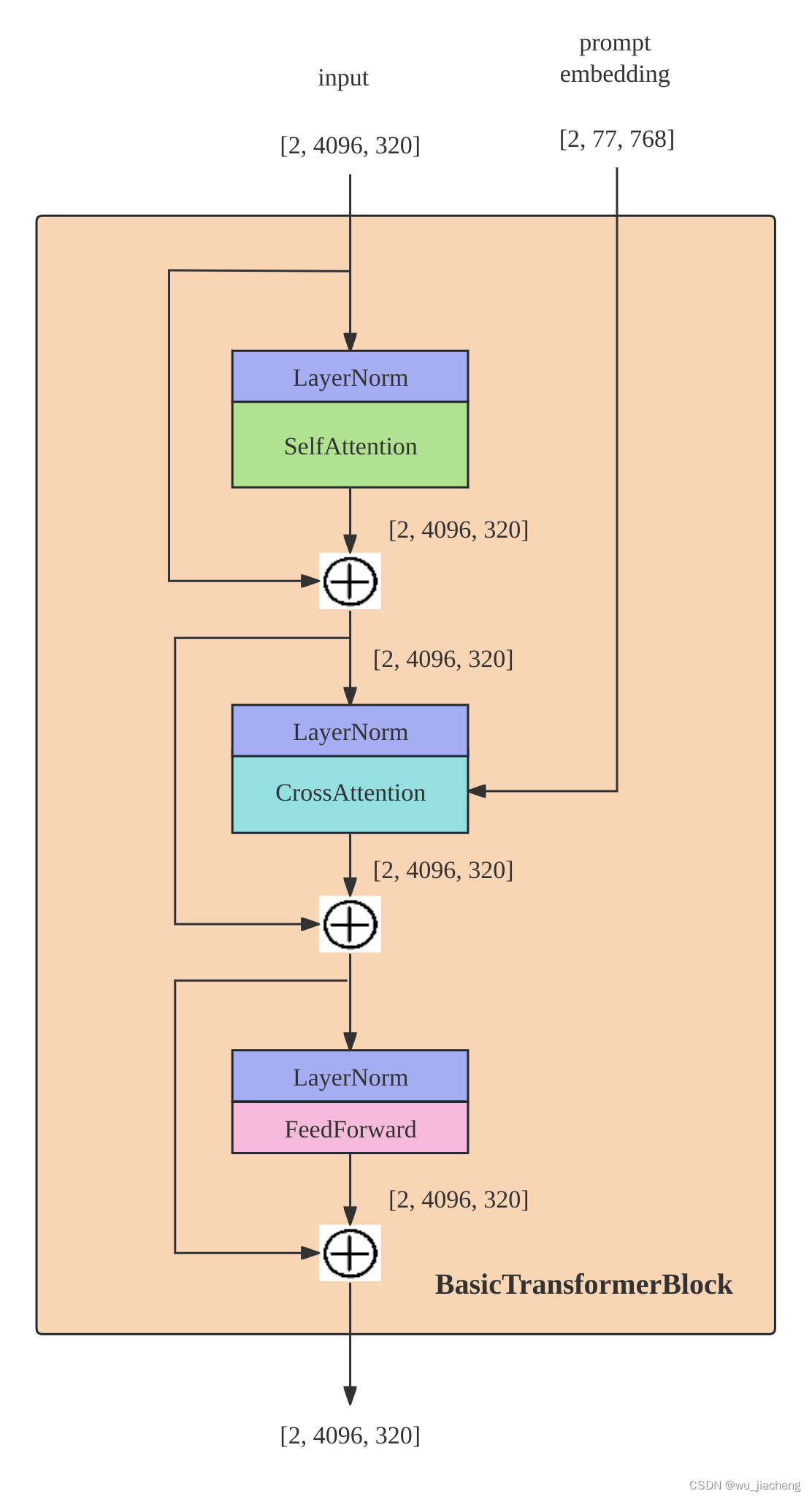
1.4.2.1.1 SelfAttention
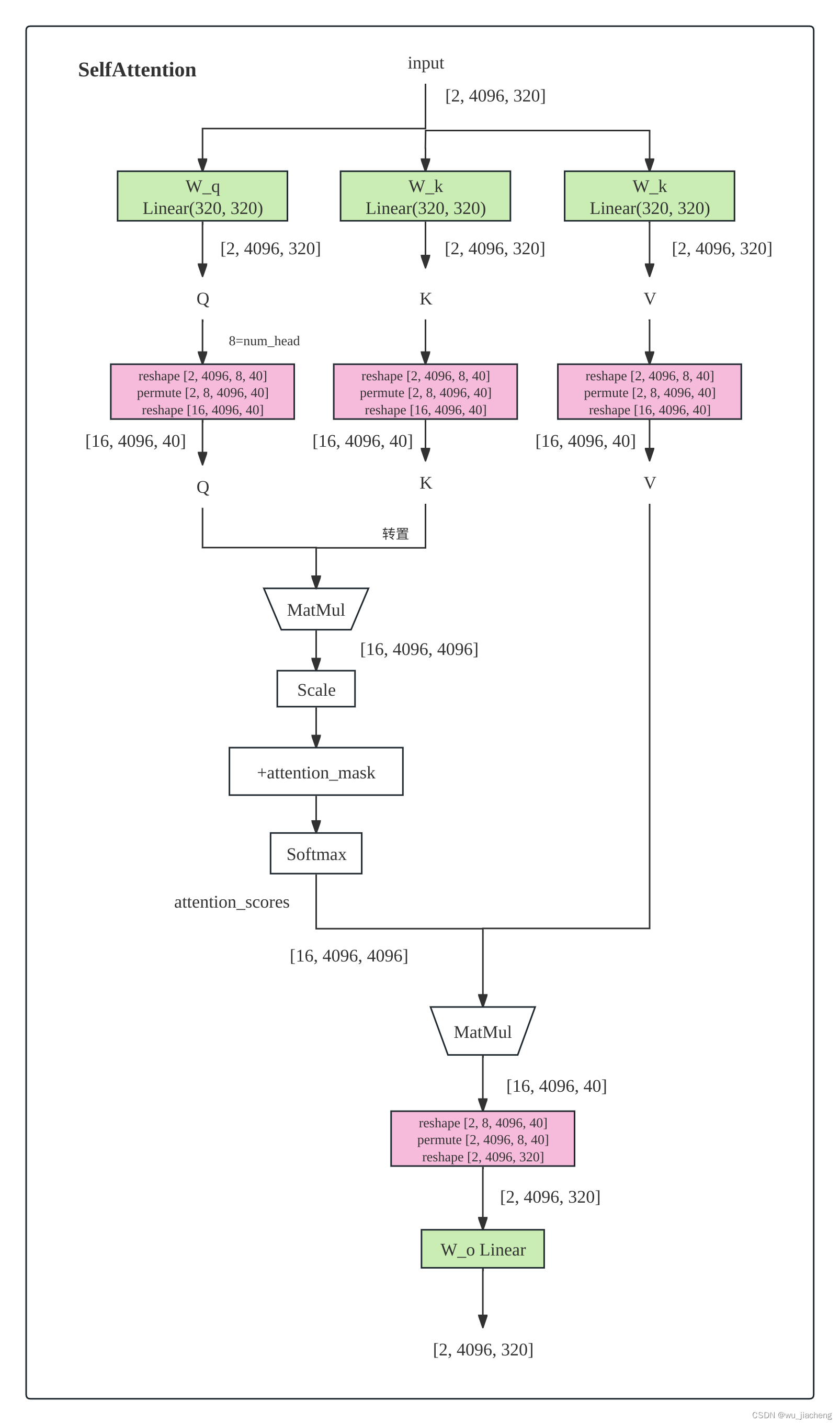
1.4.2.1.2 CrossAttention
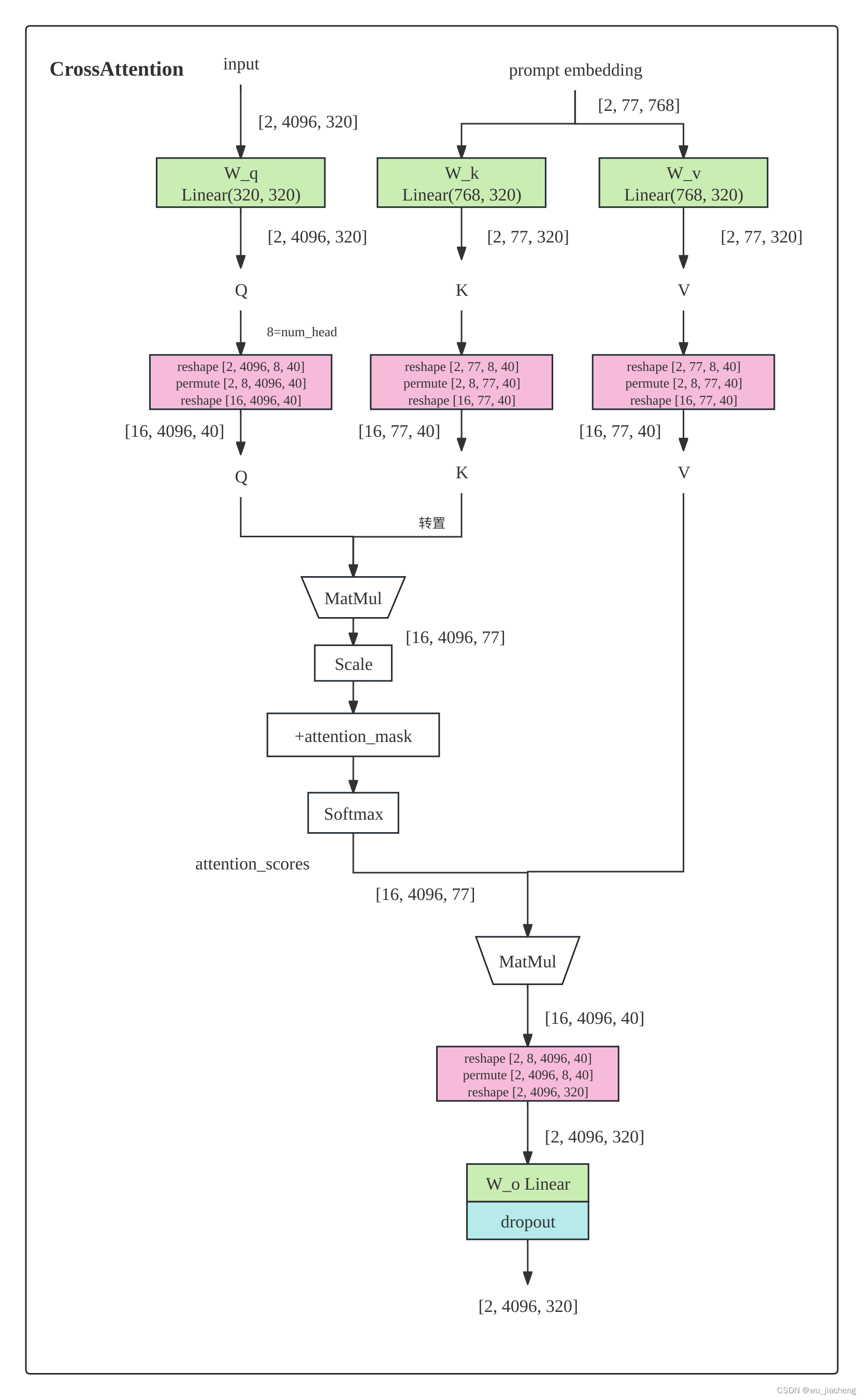
1.4.2.1.3 FeedForward

1.4.3 DownSample2D

1.5 DownBlock2D
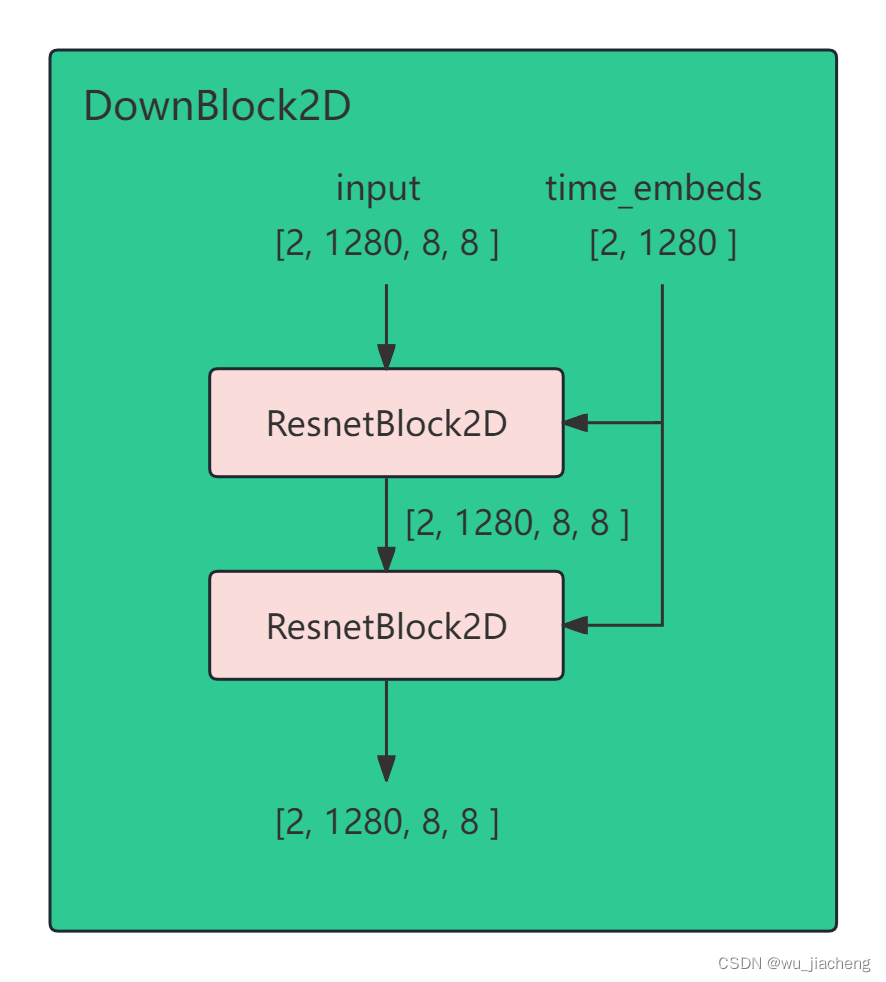
1.6 UnetMidBlock2DCrossAttn
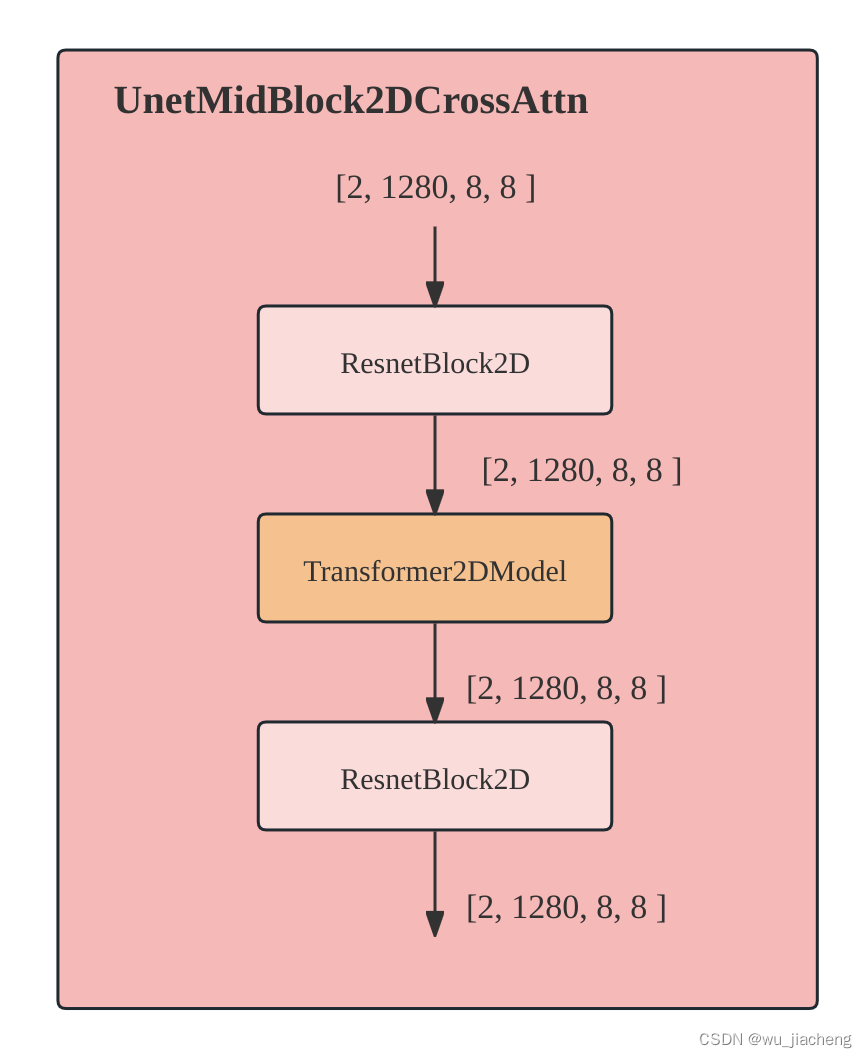
1.7 UpBlock2D
UNet右边部分的ResnetBlock2D模块,其输入除了有来自上一层的输出和time_embedd之外,还有自UNet左边部分输入,具体做法是将上一层的输出和UNet左边部分输入进行concat之后送进ResnetBlock2D模块,然后和time_embedd相加,后面的CrossAttnUpBlock2D也是如此,具体查看1.1 详细整体结构
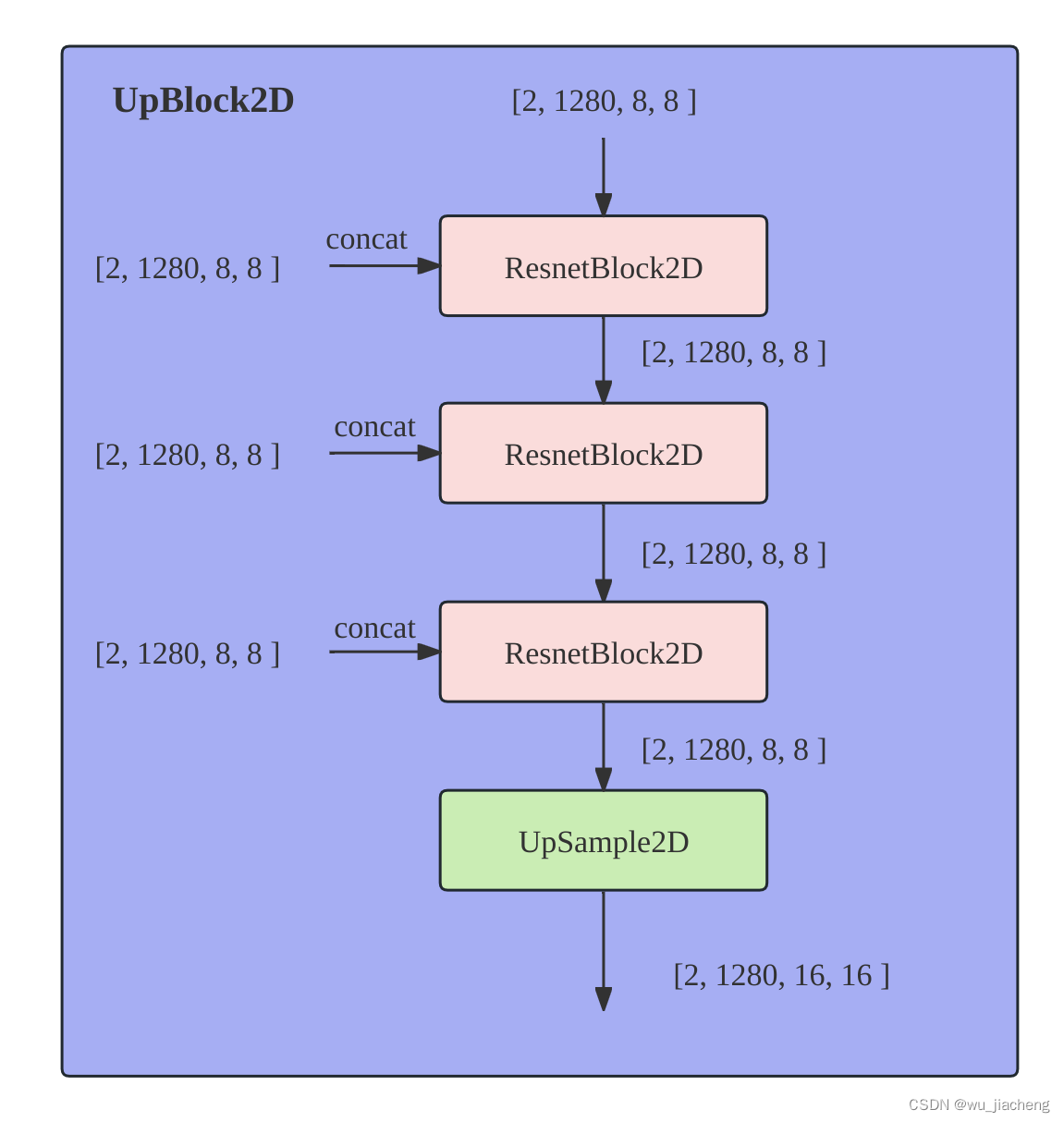
1.7.1 UpSample2D

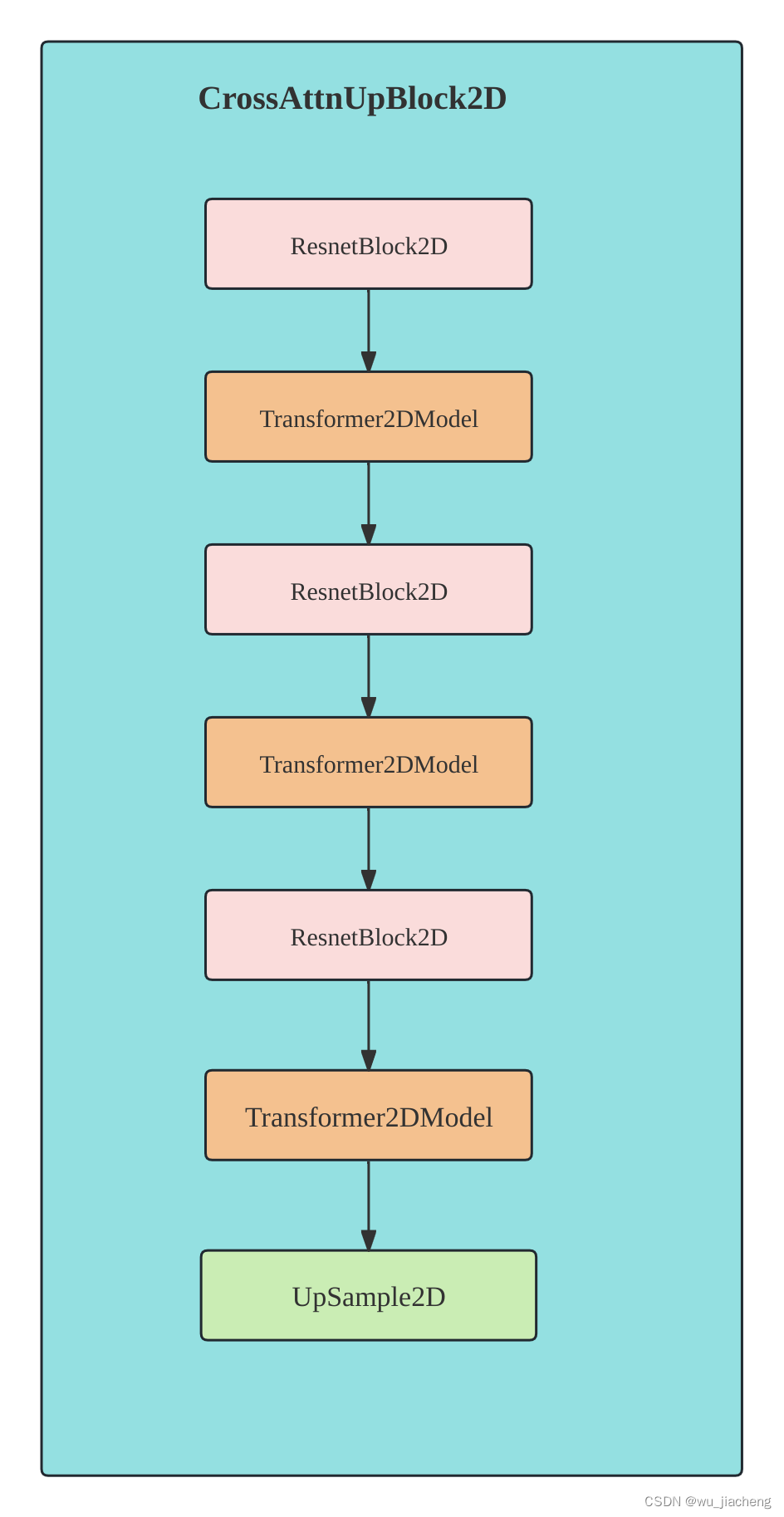
1.8 CrossAttnUpBlock2D
注意, 最后一个CrossAttnUpBlock2D没有UpSample2D模块,该模块具体输入输出shape看1.1 详细整体结构
2 VAE
2.0 介绍
将扩散过程从512x512的图像空间映射降维到64x64的潜空间,内存和运算量减小64倍
2.1 AE
注意:下面说的特征向量,编码向量,潜变量,code是同一个意思
普通的自编码器,分为编码器和解码器,编码器Encoder负责将编码图像,把图像从高维映射到低维,得到特征向量,例如把3x512x512的图像编码成4x64x64的特征向量,这个特征向量可以表示原始图像,包含原始图像的特征,比如颜色,纹理等其他抽象特征,解码器Decoder负责把低维的特征向量还原回原始图像.但这种编码是固定的,一张图片只能编码成一个固定的向量,反过来,解码也是唯一的,一个固定的编码向量只会被解码成一张确定的图像,如果来一张你训练集没见过的图片,对其编码后再解码,生成的图像大概率是个无意义的图像,因此AE是一个单值映射关系,潜变量(即编码向量)具有不连续性,潜变量是确定性值,选择一个随机的潜在变量可能会产生垃圾输出,潜在空间缺乏生成能力(即潜空间不是所有的潜变量都是有效的),
举个李宏毅老师的例子:
假设我们训练好的AE将“新月”图片encode成code=1(这里假设code只有1维),将其decode能得到“新月”的图片;将“满月”encode成code=10,同样将其decode能得到“满月”图片。这时候如果我们给AE一个code=5,我们希望是能得到“半月”的图片,但由于之前训练时并没有将“半月”的图片编码,或者将一张非月亮的图片编码为5,那么我们就不太可能得到“半月”的图片。
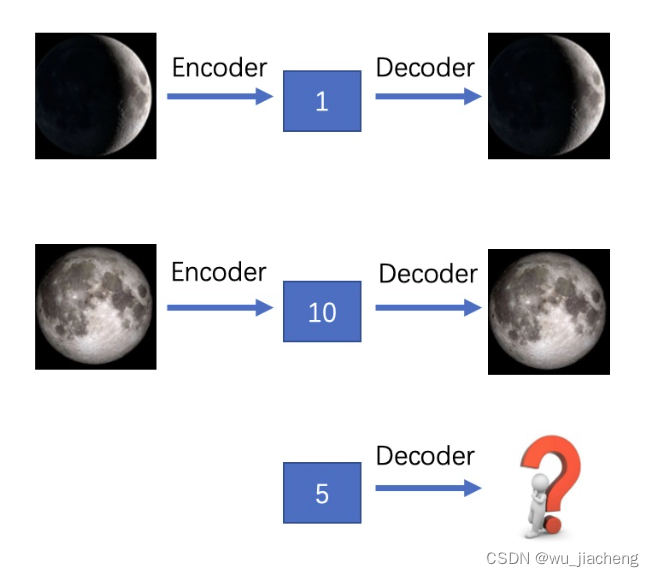
其他博客解释:
AE的Encoder是将图片映射成“数值编码”,Decoder是将“数值编码”映射成图片。这样存在的问题是,在训练过程中,随着不断降低输入图片与输出图片之间的误差,模型会过拟合,泛化性能不好。也就是说对于一个训练好的AE,输入某个图片,就只会将其编码为某个确定的code,输入某个确定的code就只会输出某个确定的图片,并且如果这个code来自于没见过的图片,那么生成的图片也不会好。
自动编码器是数据相关的(data-specific 或 data-dependent),这意味着自动编码器只能压缩那些与训练数据类似的数据,反过也是一类数据对应一种编码器,无法拓展一种编码器去应用于另一类数据。
2.2 VAE
而VAE不是将图像编码成一个固定的值,而是编码成一个连续的分布,这样,只要满足这个分布,我就能重建原始图像,满足这个分布的值会有很多,不再是一个固定的code了,例如,我把编码器的输出约束成一个标准正态分布,重建图像我只需要从标准正态分布采样在送到就解码器即可,
这里其实不一定非得要是标准正态分布,只要是连续的分布理论上都可以,但由于标准正态分布有良好的性质:1,高维正态分布采样的向量模长近似一致,两两近似正交,两点之间的欧式距离与期望值近似,这是一个很好的约束,对模型的学习有利;2,良好的数学性质,但你对多个分布进行运算时(像Diffusion),正态分布会带来很大的便利,可以通过标准化,变换等方式处理,便于模型的训练和优化;3,用标准正态分布对潜变量进行建模,能利用正态分布的性质进行随机采样和重构(重参数化)
举个例子:来自https://www.cnblogs.com/amazingter/p/14686450.html
针对上面的半月问题,我们转变思路,不将图片映射成“数值编码”,而将其映射成“分布”。我们将“新月”图片映射成μ=1的正态分布,那么就相当于在1附近加了噪声,此时不仅1表示“新月”,1附近的数值也表示“新月”,只是1的时候最像“新月”。将"满月"映射成μ=10的正态分布,10的附近也都表示“满月”。那么code=5时,就同时拥有了“新月”和“满月”的特点,那么这时候decode出来的大概率就是“半月”了。这就是VAE的思想。

关于VAE还可以参考【VAE学习笔记】全面通透地理解VAE(Variational Auto Encoder)_vae的作用-CSDN博客
写的很好,接下来正式上图
2.3 整体结构
由于csdn查看大图很捞,可双击另存为查看高清大图
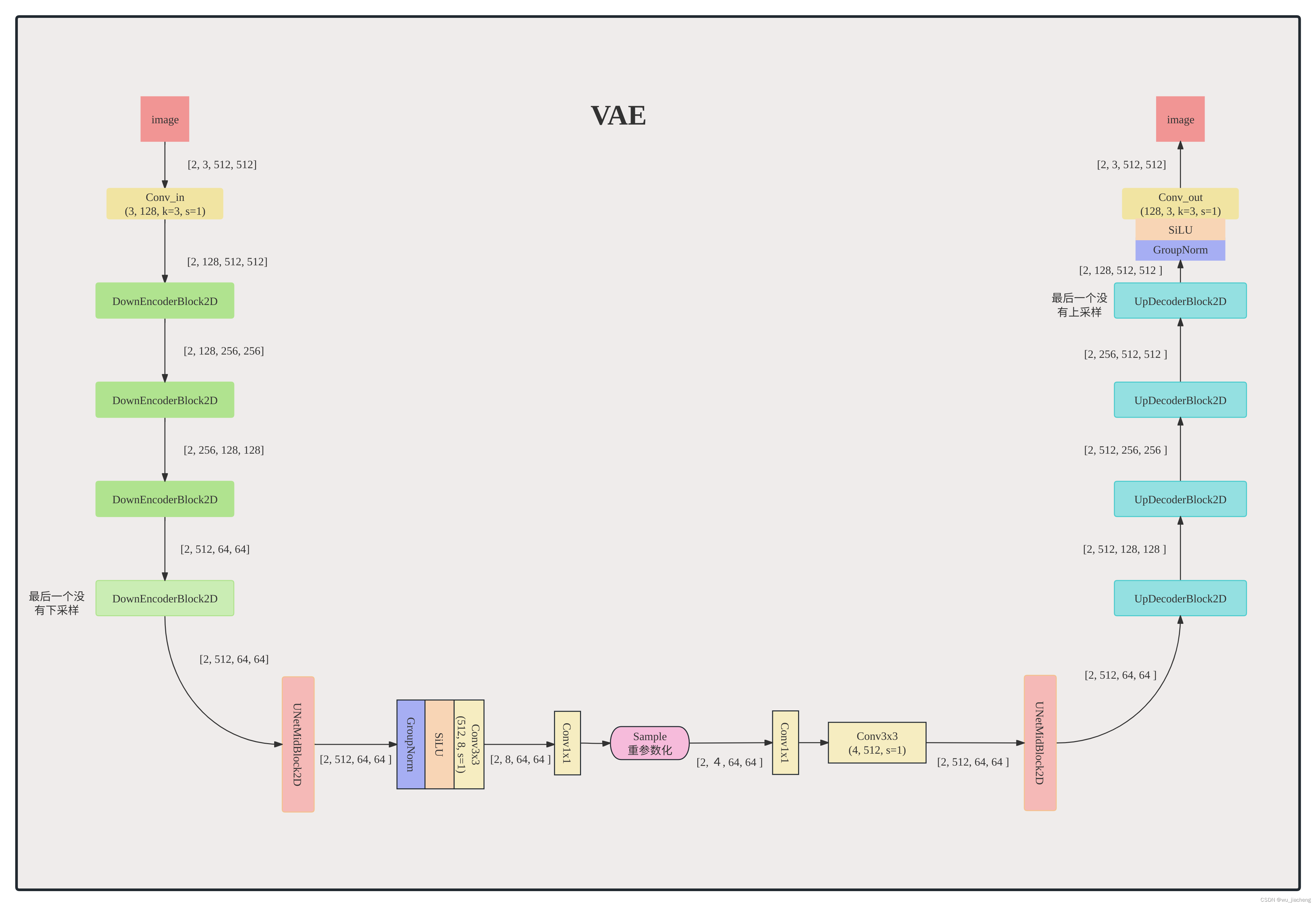
2.4 DownEncoderBlock2D
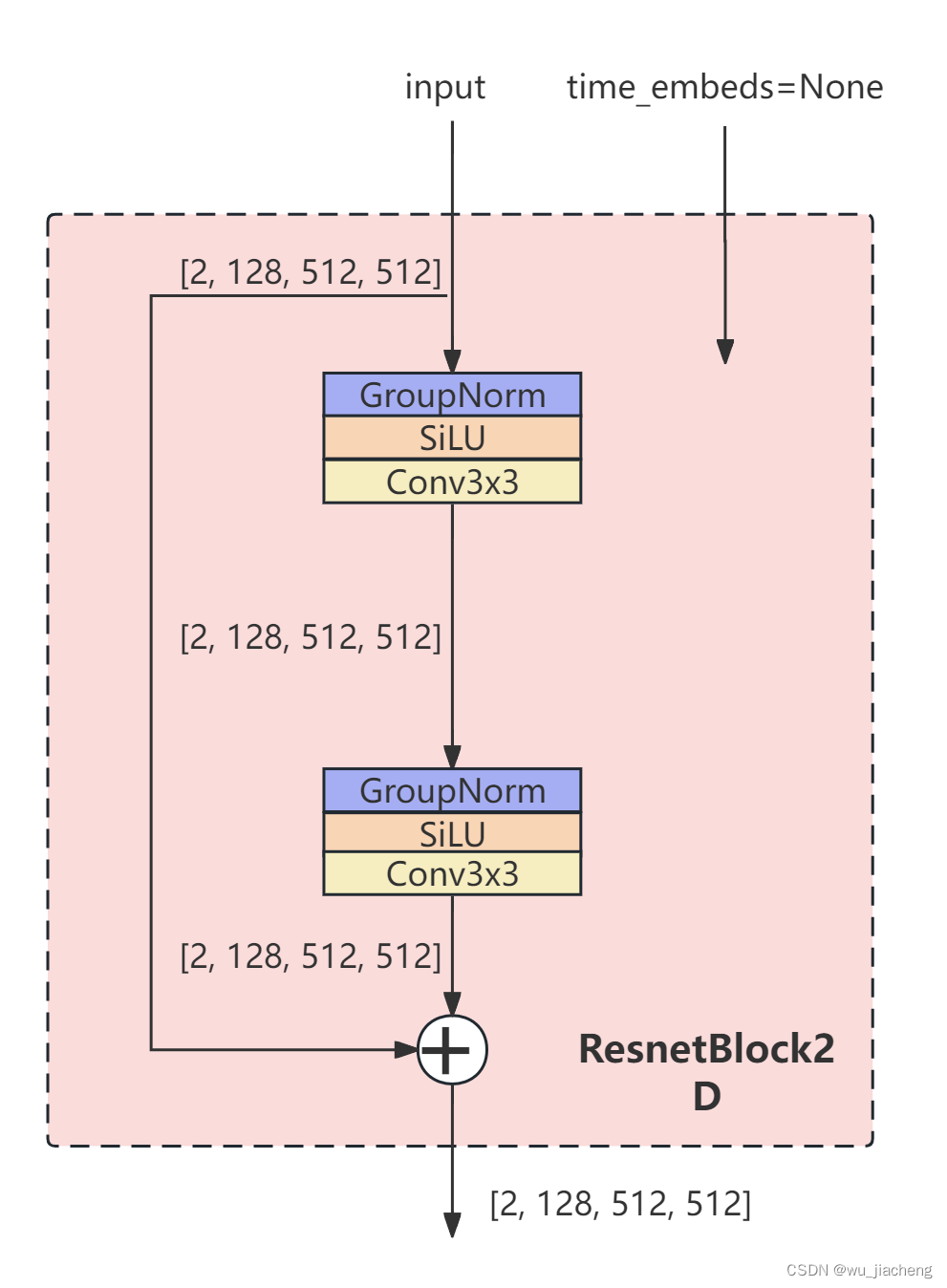
注意:VAE的ResnetBlock2D模块是没有时间步的输入的,即time_embeds=None, 其他的和上面Unet中的ResnetBlock2D一致
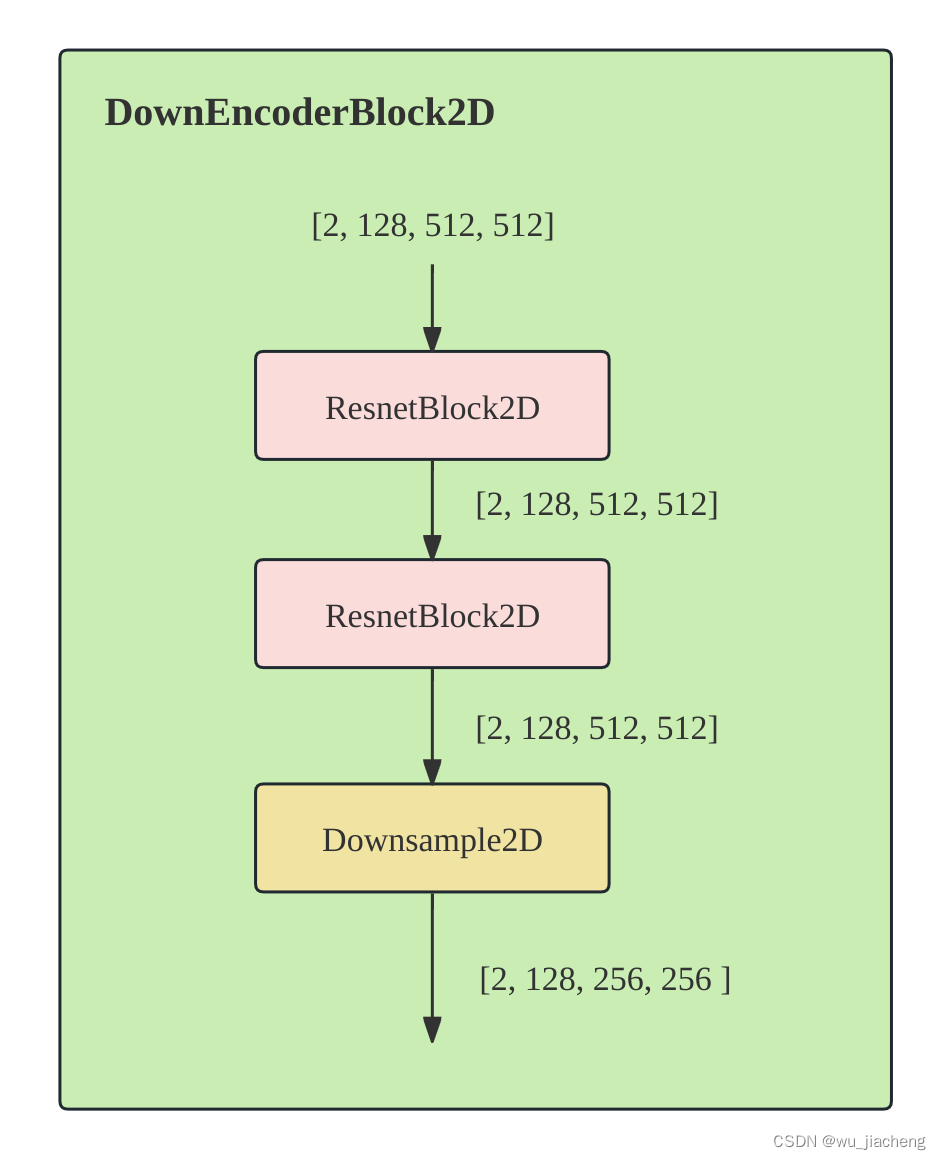
2.4.1 ResnetBlock2D
2.4.2 UpSample2D

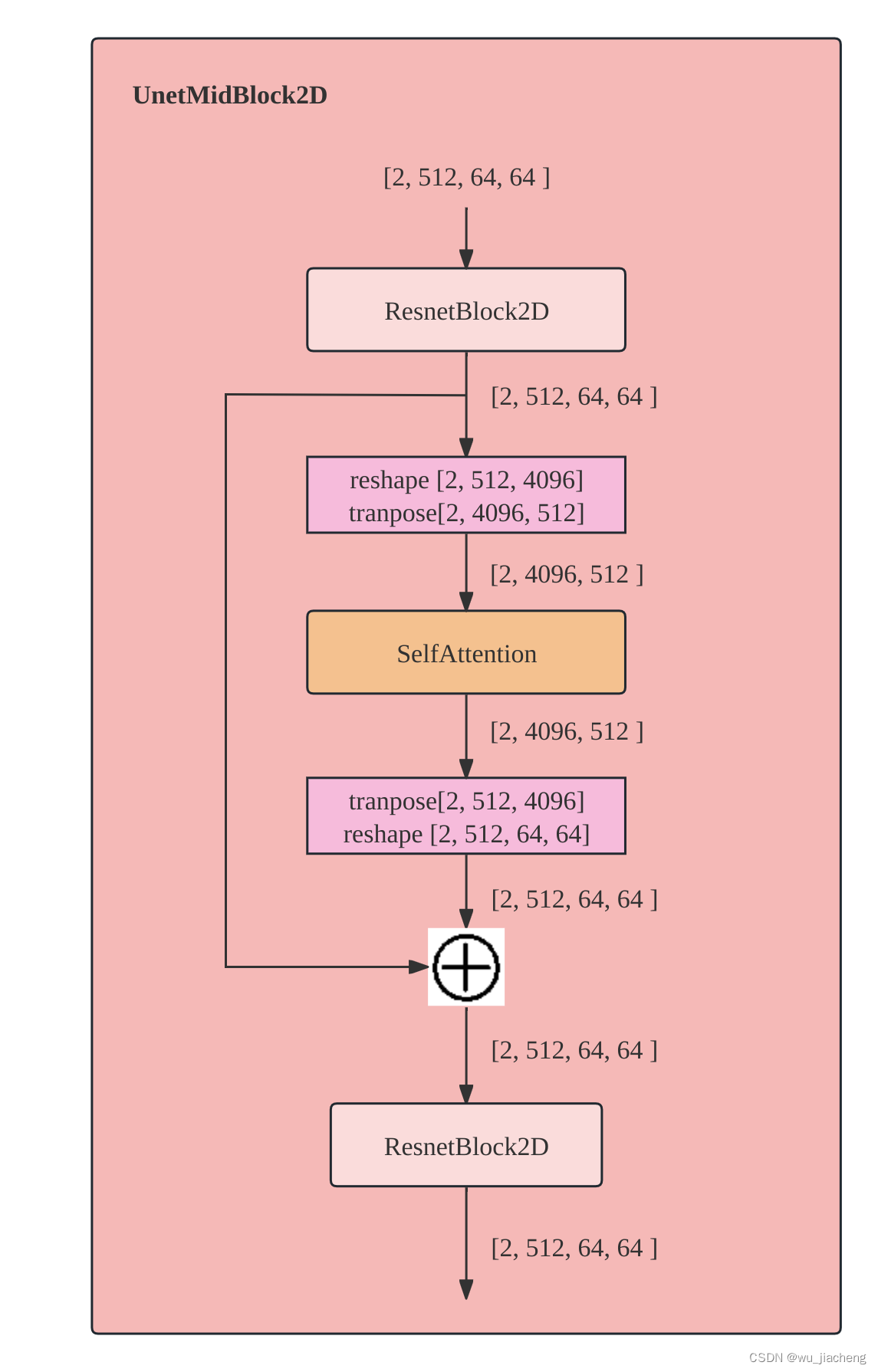
2.5 UnetMidBlock2D
SelfAttention参考Unet中的
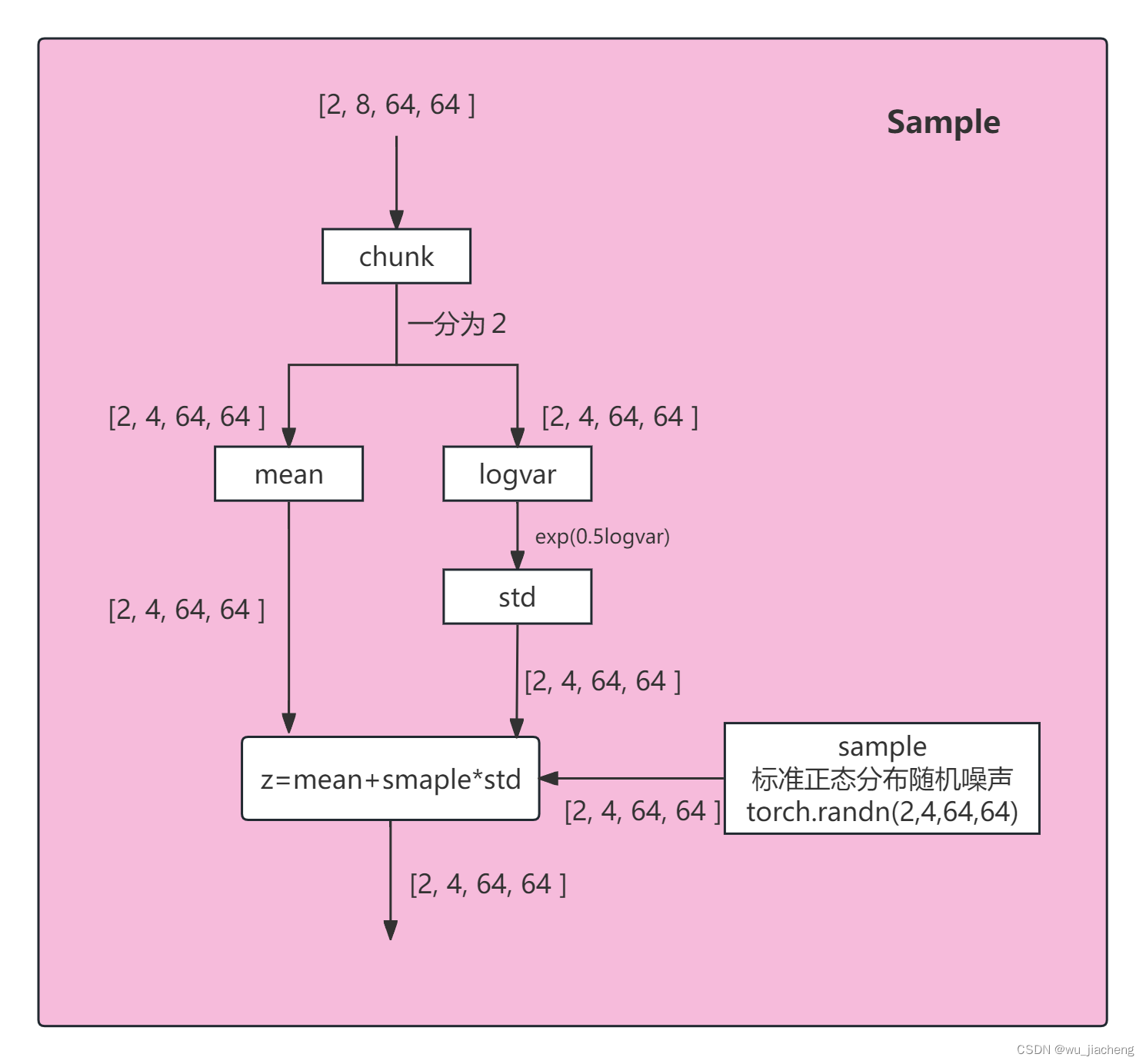
2.6 Sample
重参数化技巧:
现在均值mean和方差var(实际是log方差,这里先以方差为例)是网络的输出,也就是现在编码器的输出服从N~(mean, var)这个正态分布,我们要从这个正态分布采样出一个样本,送进解码器,这个样本是服从N~(mean, var)正态分布的,但采样这个操作是不可导的,采样操作是指从某个概率分布中随机抽取样本的过程,因为梯度是损失函数关于模型参数的变化率,而采样操作的非确定性使得无法直接计算关于参数的精确梯度。如果将采样操作视为一个具有参数的函数,并尝试计算其导数,通常会遇到两个问题:
-
不可导性: 由于采样操作引入了离散性和不可导性,它们在大多数情况下是不可导的。导数描述的是函数在某一点上的变化率,而采样操作在这方面表现得很突变和不连续,因此没有明确定义的导数。
-
梯度的方差: 即使我们忽略不可导性,尝试使用梯度信息来更新参数,由于采样引入的随机性,梯度的方差可能会非常高,导致不稳定的优化过程。
所以无法对mean和var求偏导,因为这里mean和var就是网络的参数,这个时候可以从标准正态分布N(0,1)采样一个sample(一般会用概率密度的分布函数去采样), 这个时候sample就是一个确定的值,把sample当成常数,std是标准差,等于var开根号
令z=mean + sample * std,这个时候z就可以对mean和std求偏导了,z就等价从N~(mean, var)这个分布采样,可以对z求期望和方差,根据高斯分布的性质以及期望和方差的公式,能得出z也服从正态分布,切均值=mean, 方差=std的平方=var,这样做其实是把随机性转移到了sample这个常数
但代码里是log方差,是因为方差是正的,加log让它取值范围也能取负值,这样就不用加激活函数了,所以后面再用exp还原方差
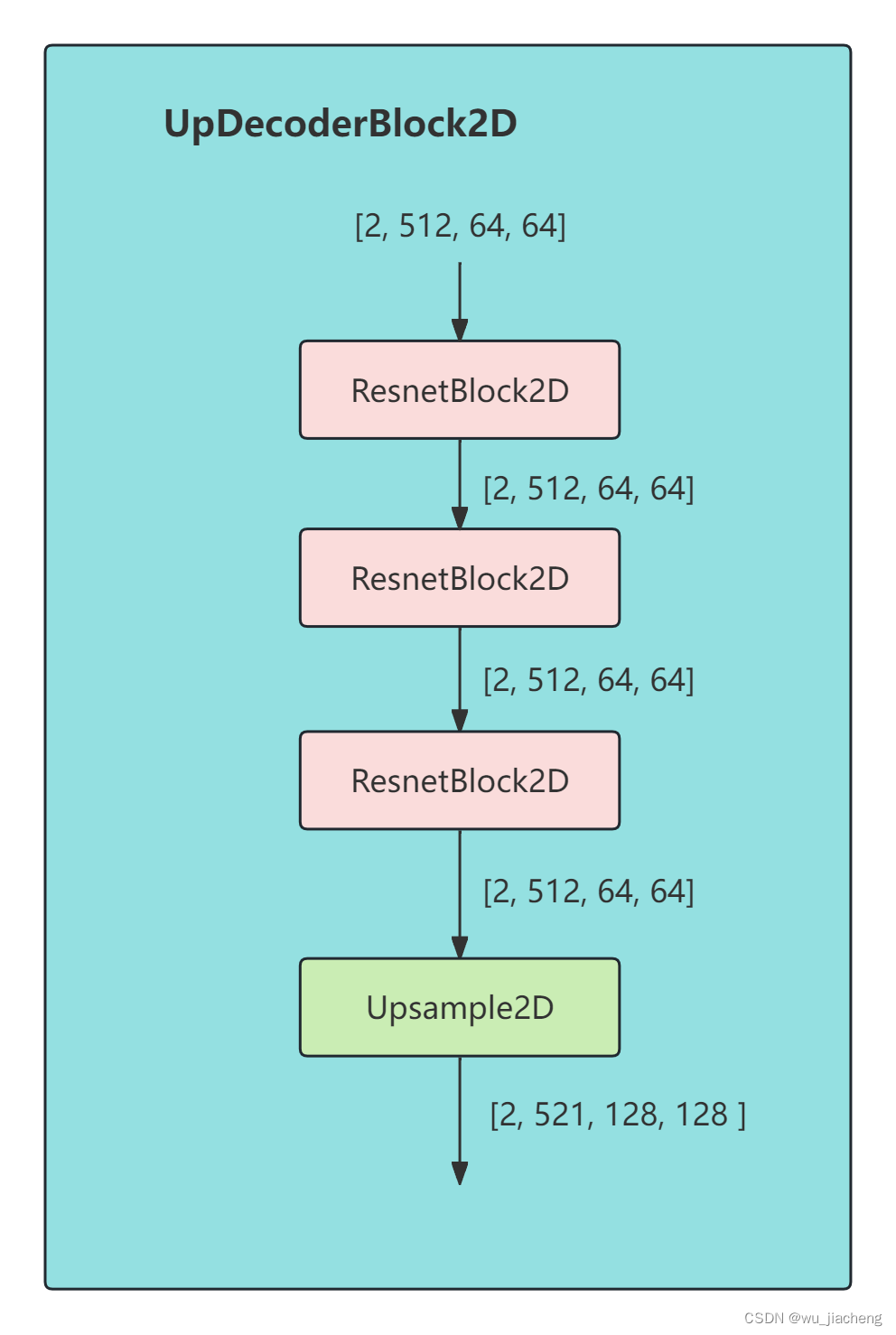
2.7 UpDecoderBlock2D
2.7.1 UpSample2D