向量内积（点乘/点积/数量积）：两个向量对应元素相乘之后求和：
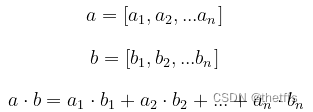
CPU实现：
//cpu 实现一下向量内积#include<stdio.h>
template<typedef T>
void dot_mul(T *a, T *b, T *c, int n)
{ double tmp = 0;for(int i = 0; i < n; i++){tmp += a[i] * b[i];}*c = tmp;
}int main()
{//定义数组以及数组的大小float a[N], b[N];float c = 0;for(int i = 0; i < N; ++i){a[i] = i * 1.0;b[i] = 1.0}dot_cpu(a, b, &c, N);printf("a dot b output %f\n", c);printf("Hello World!\n");首次接触bank conflict的概念，在这里补充一下。
bank是shared memory中用来存储数据的特殊组织方式。为了高效存取输入shared memory分为32个存储体(bank)， 对应32个线程。每个bank有一个固定的带宽，可以同时服务一个线程的访问。当多个线程在一个时钟周期内访问一个bank的不同地址时，会产生bank conflict。因为bank的读取带宽不能高效的同时服务多个线程，因此需要需要解决bank conflict。有个不解的地方，是什么导致所有的thread都去访问同一个bank？
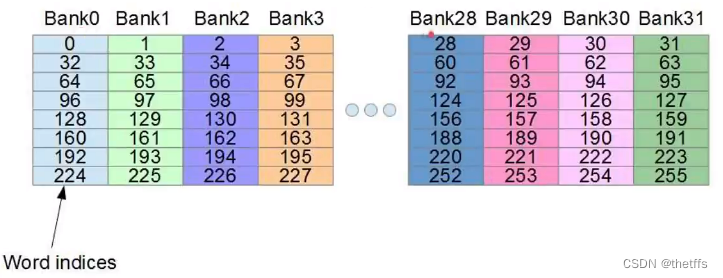了解一个bank的属性：bank的宽度是指bank存储器的位宽。位宽是存储器连接的总线一次可以传数的数据量，可以是32bit，也可以是64bit，取决于总线的位数。可以是4字节/8字节。
避免bank conflict的方法有以下几种：
- 使用不同的bank size，可以通过cudaDeviceSetSharedMemConfig函数来设置bank size为4字节或8字节，这样可以改变shared memory到bank的映射方式，减少冲突的可能性。
- 使用memory padding，即在shared memory的数组中增加一些空白的元素，使得不同的线程访问不同的bank，从而避免冲突。
- 使用不同的访问模式，比如使用转置或者重排的方式，使得一个warp中的线程访问不同的bank或者同一个地址，从而避免冲突。
回归正题，用cuda实现向量的内积(点积/点乘/数量积)。
单block分散归约法
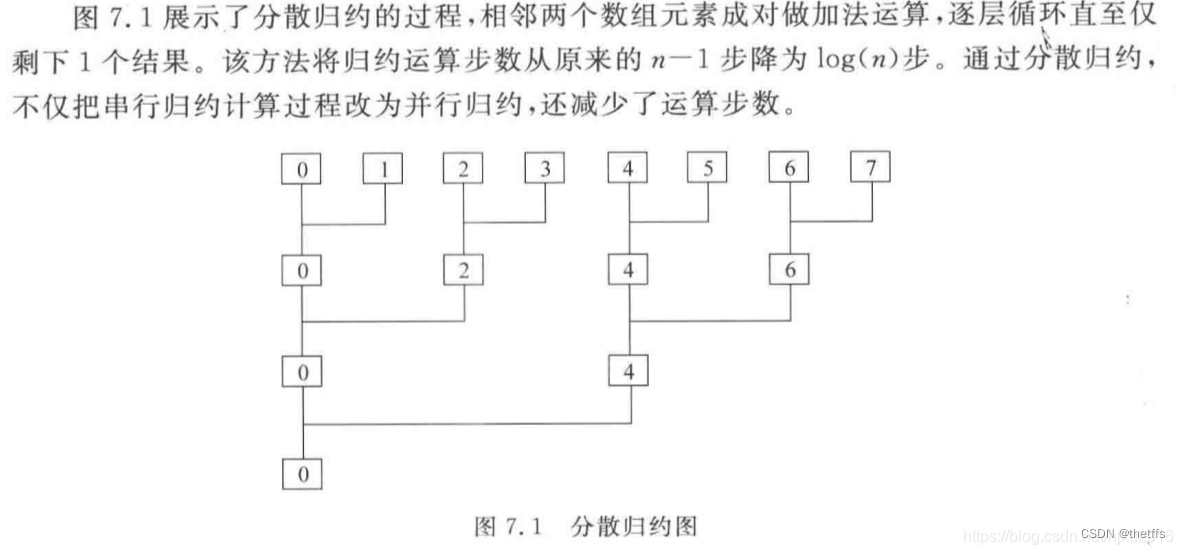
第一次理解单block分散归约 takes 3 hours!
第一次手撸整理单block分散归约代码 takes one and a half hours!
main 函数 takes half an hour !
以下是我学习整理后的kernel函数：
#include "cuda_runtime.h"
#include "stdio.h"#define threadnums 32
#define N 2048//单block分散归约法
template <typedef T>
__global__ dotmul_gpu_1(T *a, T *b, T *c, int N)
{const int nThreadIdx = threadIdx.x;//当前线程ID索引const int nBlockDimX = blockDim.x;//一个block内开启的线程总数int nTid = nTreadIdx;dobule dTmp = 0.0;//开辟shared memory,大小与线程数量一致__shared__ T tmp[nBlockDimX];//step 1://每个线程负责 N/nBlockDimX 个元素相乘后的累加 while(nTid < N){dTmp += a[nTid] * b[nTid];nTid += nBlockDimX;}//每个线程将以上计算结果放入共享内存中tmp[nThreadIdx] = dTmp;//同步线程，等待所有线程完成以上计算__syncthreads();//step2:归约reductionint i = 2;int j = 1;while(i <= nBlockDimX){if(nThreadIdx / i == 0){//所有线程完成一次求和归约计算dTmp = tmp[nThreadIdx] + tmp[nThreadIdx + j];tmp[nThreadIdx] = dTmp;}__syncthreads();//这个地方利用i和j进行索引比较巧妙//32个线程进行求和归约，每次归约，线程索引的元素下标如下：//第一次归约：0+1, 2+3, 4+5, 6+7, 8+9, 10+11， 12+13，14+15, 16+17, 18+19, 20+21, 22+23, 24+25, 26+27, 28+29, 30+31//第二次归约：0+2, 4+6, 8+10， 12+14, 16+18, 20+22, 24+26, 28+30 //第三次归约：0+4, 8+12, 16+20, 24+28//第四次归约：0+8, 16+24//第五次归约：0+16//求和归约值：0i *= 2;j *= 2;}//此处只在一个线程中获取向量内积值，因此需要线程ID判断if(0 == nTreadIdx)*c = tmp[0];
}主函数整理如下：
int main()
{float a[N], b[N];//对向量a[], b[]初始化值for(int i = 0; i < N; i++){a[i] = 1.0;b[i] = i * 1.0;}float *d_a=NULL, *d_b=NULL， *d_c=NULL;//将数组a[]的数据从CPU拷贝到GPUcudaMalloc(&d_a, N*sizeof(float));cudaMemcpyAsync(d_a, a, N*sizeof(float), cudaMemcpyHostToDevice);//将数组b[]的数据从CPU拷贝到GPUcudaMalloc(&d_b, N*sizeof(float));cudaMemcpyAsync(d_b, b, N*sizeof(float), cudaMemcpyHostToDevice);//不要忘记了结果也需要存储在显存上!cudaMalloc(&d_c, sizeof(float));//调用kernel函数dim3 blocks(1,0,0);dim3 threadPerBlock(threadnums, 0, 0);dotmul_gpu_1<<<blocks, threadPerBlock>>>(d_a, d_b, d_c, N);//分配的显存需要手动释放cudaFree(d_a);cudaFree(d_b);cudaFree(d_c);return 0;
}参考链接：
CUDA学习(十)：向量内积的多种方法实现_为向量类增加计算内积的功能。-CSDN博客
拯救你的CUDA！什么是bank，为什么会发生bank conflict？？？_哔哩哔哩_bilibili
该方法存在的问题在参考文章中被指出有违背访问对其原则、容易产生bank conflict。后面再一一学习补充。
此外，解决cuda上向量内积的方法还有，留待后续学习补充：
