343. 整数拆分

题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

求解思路：

动规五部曲

1. 确定dp数组及其下标含义：dp[i] 拆分i，可以得到的最大乘积为dp[i]
2. 确定递推公式：从1开始遍历j，有两种渠道得到dp[i]，一种是 j * (i - j)，另一种是 j * dp[i - j]，相当于拆分 (i - j)；注意dp[i] 本身也要作为取最大值中的一个
3. dp的初始化：dp[0] 和 dp[1] 都是没有意义的，只需要初始化 dp[2] = 1
4. 确定遍历顺序：递归公式为 dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))，dp[i] 依靠 dp[i-j]，所以从前向后遍历；注意枚举 j 是从1开始的，并且如果拆分一个数使乘积最大，那么一定是拆分成m个近似相同的子数，因此 j 遍历到 i/2 就可以了
5. 举例推导dp数组：当n为10的时候，如图所示

代码：

class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1);dp[2] = 1;for (int i = 3; i <= n; i++){for (int j = 1; j <= i/2; j++){dp[i] = max(dp[i], max((i-j)*j, dp[i-j]*j));}}return dp[n];}
};

96.不同的二叉搜索树

题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

求解思路：

动规五部曲

1. 确定dp数组及其下标含义： 1到i为节点组成的二叉搜索树的个数为dp[i]
2. 确定递推公式：dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]，即dp[i] += dp[j - 1] * dp[i - j];
3. dp数组的初始化：dp[0] = 1
4. 确定遍历顺序：节点数为i的状态是依靠 i之前节点数的状态，因此从前向后遍历
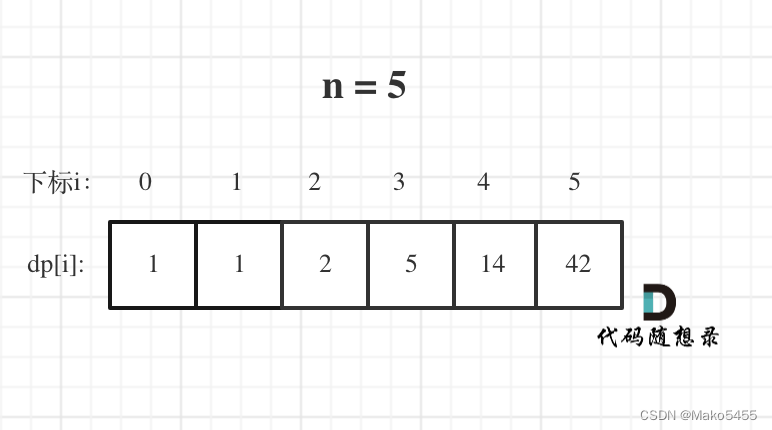
5. 举例推导dp数组：以n=5为例，如图所示

代码：

class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0] = 1;for (int i = 1; i <= n; i++){for (int j = 1; j <= i; j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};