NEJM一篇新文为例，聊聊孟德尔随机化研究mr

2019年3月14日，新英格兰医学杂志发表了一篇论著，Mendelian Randomization Study of ACLY and Cardiovascular disease, 即《ACLY和心血管疾病的孟德尔随机化研究》。与小咖在2017年1月9日报道的一篇发表在新英格兰医学的孟德尔随机化研究——精读NEJM：基因变异与冠心病/糖尿病的发病风险，是同一个团队的成果。

本篇文章意在简单介绍ACLY这篇文章的脉络，并梳理孟德尔随机化研究的基本原则。

研究背景

ATP柠檬酸裂合酶（ATP citrate lyase，此后简称ACLY）是胆固醇生物合成途径中的一种酶，此酶的作用位置在3-羟基-3-甲戊二酸辅酶A还原酶（HMGCR，他汀类药物靶点）的上游。

研究者提出的科学问题是：通过抑制ACLY来降低低密度脂蛋白（LDL），是否可以达到与HMGCR抑制剂相同的减少心血管疾病事件的效果。

Bempedoic Acid 是一种口服的ACLY抑制剂。在名为CLEAR的临床试验中，在受试者已经接受他汀类治疗的情况下，服用Bempedoic Acid组的LDL水平较基线水平降低，且比安慰剂组的下降幅度要多18.1个百分点。虽然与安慰剂组相比，Bempedoic Acid组的心血管事件数目降低，但心血管疾病造成的死亡数和癌症数目却增加了。

由此引发疑问，Bempedoic Acid这种ACLY抑制剂或者其他ACLY的抑制剂是否会带来巨大的负面效应。

所以，研究者想利用模拟ACLY抑制剂效应的遗传变异和模拟HMGCR抑制剂效应的遗传变异，来比较两者对LDL和临床结局的影响，进而评估通过ACLY抑制来降低LDL所产生的临床效应。

考虑到Bempedoic Acid可能和他汀类药物或依折麦布（ezetimibe）联用，研究者还评估了ACLY变异与另外两种变异联合作用的效果，这两种变异名为 HMGCR 和 NPC1L1，分别编码他汀类药物和依折麦布的靶点蛋白。这一研究旨在为ACLY抑制剂的效应提供生物学背景信息。

研究方法

分别用编码ACLY和HMGCR的基因中的变异构建遗传分数作为工具变量，工具变量可以模拟ACLY抑制剂和HMGCR抑制剂的效应。研究者比较了遗传分数与血脂水平、血脂蛋白水平、心血管事件风险和癌症风险的关系。

研究结果

总共654783名参与者纳入研究（包括105429名伴有主要心血管事件）。ACLY遗传分数和HMGCR遗传分数与血脂水平、血脂蛋白水平变化有着相同模式的关联，与心血管事件的风险有着相同效应的关联。

对于ACLY遗传分数来说，LDL水平每降低10mg/dL，心血管事件的风险相应降低17.7%（OR值为0.823，95%置信区间为0.78-0.87，P=4.0×10-14）。

对于HMGCR遗传分数来说，LDL水平每降低10mg/dL，心血管事件的风险相应降低16.4%（OR值为0.836，95%置信区间为0.81-0.87，P=3.9×10-14）。ACLY抑制和HMGCR抑制都不与癌症风险增加有关。

文章主要大的框架如下图所示

图1：本文的框架

除此之外，文章还应用ACLY遗传分数和HMGCR遗传分数结合，ACLY遗传分数和HMGCR遗传分数结合，做了因子孟德尔随机化研究（Factorial Mendelian randomization）。本文旨在讲明孟德尔随机化研究的基本原则，在此处不再过多展开。小咖2017年初关于孟德尔随机的文章中详细解释了这种因子孟德尔随机化研究。(精读NEJM：基因变异与冠心病/糖尿病的发病风险)

我们可以用随机对照分组试验的设计思路来帮助理解孟德尔随机化研究的原理（比较可见图2）。孟德尔随机化研究的使用背景是研究人员无法确认暴露对于结局的效应（可能是有混杂因素，也可能是“暴露”和“结局”的实际关系为因果倒置，或者常规的随机对照分组试验面临伦理风险而难以进行，比如CLEAR研究发现ACLY抑制剂组有可能会带来更多的风险）。

它的假设是基因在减数分裂时随机分配到子代，这就相当于把基因的效应随机分配给“受试者”，从而“控制”其他因素对基因效应的影响。研究者运用基因变异作为工具变量研究工具变量和结局的关系，由这两者的关系来推出暴露（基因效应）对于结局的效应。

图2：孟德尔随机化研究和随机对照分组试验的对比（图片来源：https://www.acc.org/latest-in-cardiology/articles/2015/06/11/13/17/mendelian-randomization-studies）

有一个研究例子可以帮助我们理解，该研究的目的是关于低水平血浆胆固醇浓度和癌症风险的关系。在80年代中期存在一个争议：低血浆胆固醇水平是否会直接增加癌症风险。有人推测，可能是癌症导致了胆固醇水平降低（因果倒置），也有可能有饮食等混杂因素同时作用于胆固醇水平和癌症的风险。

为了验证两者是否存在直接的因果关系，一位叫Katan的研究者巧妙利用了一种叫 ApoE2 的基因变异，该变异会导致低水平胆固醇。Katan的想法是，ApoE2 变异的携带者出生时就拥有更低的胆固醇水平，这些携带者和其他正常ApoE 基因的携带者不会有系统性的差异，因此ApoE 基因到胆固醇水平的因果关系上应该不存在混杂因素。

类比到传统的随机对照分组试验中，不同基因的携带者即对应着被随机分配到不同处理中的受试者。如果低胆固醇水平是癌症风险增高的直接原因，那么与非癌症对照组相比，癌症病人中 ApoE2 的携带者比例将会更高。反之，癌症病例组和对照组，ApoE 基因分布情况应该大致相同。

ApoE 基因的变异会导致胆固醇浓度降低，因此 ApoE 变异可以作为工具变量，在新英格兰的文章中对应的是ACLY遗传分数。胆固醇浓度即为风险暴露，在本文中对应的点是ACLY抑制效应。癌症即为结局，在本文中对应的点是心血管事件风险（关系可见图3）。

本文设想到有的读者对混杂因素（confounding factors）这个概念可能不太熟悉，想稍微介绍一下。混杂因素同时与暴露和结局有关联，所以通过观察性数据得到的暴露和结局的关系，并非是暴露和结局的单纯关系，还掺杂着混杂因素对两者关系的影响。所以为了揭示暴露和结局的真正关系，必须考虑可能存在的混杂因素。

对应到ACLY的研究中，研究者为了阐明ACLY抑制（暴露）与心血管事件风险（结局）之间的关系，首先分析证明ACLY遗传分数与ACLY抑制（暴露）有很强的关联性，然后应用ACLY遗传分数作为工具变量，得出ACLY遗传评分和心血管事件风险（结局）的关系，从而解答研究问题。

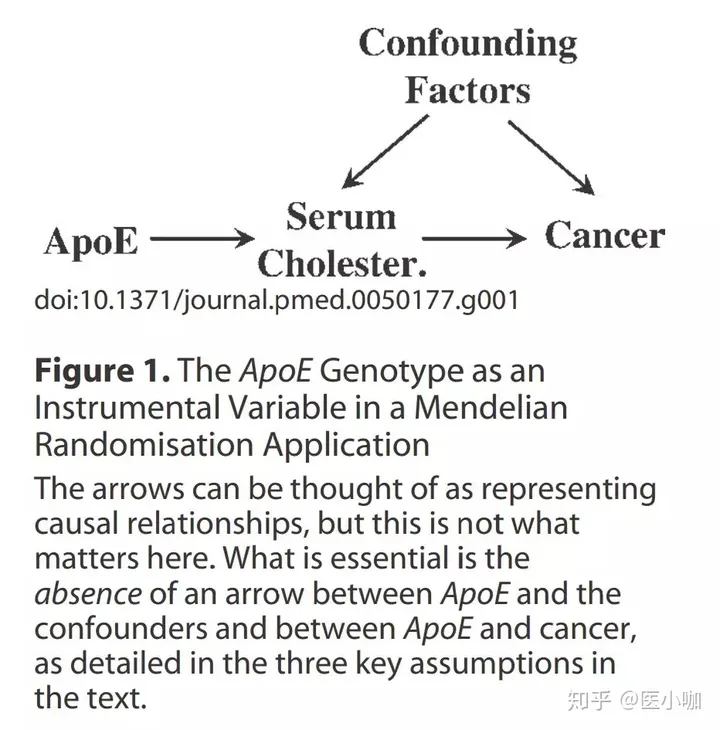
图3：综述上的例子

其中，若遗传变异可以作为工具变量，需要满足以下三个假设：

1. 基因变异（ ApoE 变异）与混杂因素（Confounding Factors）不相关。

2. 基因变异（ ApoE 变异）与暴露（低胆固醇水平）直接的关联可靠。

3. 基因变异（ ApoE 变异）只通过暴露（低胆固醇水平）这条途径影响结局（癌症），没有其他的通路，或者其他中介者使基因变异的效应作用于结局。

第一条和第三条假设其实是无法用统计学的方法完全证实的，因为有的混杂因素是无法观察得到的。好在孟德尔随机分析是建立在基因在减数分裂时随机分配到下一代个体的假设上，因此基因的效应较少受到混杂的影响。

第三条假设也应该建立在对于整个体系生物学背景的理解下，需要一些临床经验。第一条和第三条涉及到孟德尔随机化研究的一个局限性，就是作为工具变量的基因变异的作用可能存在多向性（pleiotropy），即基因变异通过其他除暴露之外的途径作用于结局。

那收集的基因变异和结局的观察性数据显示的两者联系，将不单纯是基因通过暴露作用于结局的关系。多向性很难完全检测到，但统计上有方法可以帮助检测。有文章提到过，可以检查基因变异与暴露和结局的回归模型中的残差（residual）有无相关性，若有，则提示该基因变异对于暴露和结局的关系可能存在多向性的问题。

而第二条假设是可以通过观察性的数据验证的，两者关联越强越好。若是用全基因组关联分析（GWAS）去寻找可作为工具变量的基因变异，那么理想的显著性水平应设置为5×10-8。工具变量可以是单个变异位点（单核苷酸多态性），也可以是复合多个位点的遗传分数。

在新英格兰的文章中，作者用了9个变异来构建ACLY的遗传分数，单个的变异和LDL水平（即ACLY抑制效应）的关系实际上是不强的，但9个变异构建的ACLY遗传分数却和LDL水平强相关（robustly associated）。在用多个变异来构建遗传分数时也有讲究，通常这些变异之间的关联性是低的，也即是这类文章中常提到的低连锁不平衡（linkage disequilibrium）。

在三条假设满足的前提下，若基因变异和暴露的关系、基因暴露和结局的关系呈线性，那则可以通过数学乘除的方法，得到暴露和结局的因果效应（暴露对于结局的效应=工具变量对结局的效应/工具变量对暴露的效应）。

在实际操作中，也可以直接使用两阶段最小二乘法（Two-Stage Least Squares）去估计暴露对于结局的因果效应。这一方法可以通过统计软件Stata实现。这个方法的使用有它的限制条件，有兴趣的朋友可以搜索相关的文献进行了解。（还可以查看医咖会既往发的一篇文章：控制混杂因素，再给你支个大招：工具变量分析）

其实孟德尔随机化研究不是完美的。虽然在孟德尔第二定律中不同位点的等位基因是随机遗传给子代的，但这并不适用于所有基因位点。当同一染色体上的两个基因位点位置比较靠近，那么它们一起遗传的几率会增大，也就是连锁不平衡现象。其次，不同人群中的等位基因频率（allele frequency）和疾病流行率（prevalence）可能不一样，因此若研究对象是混杂的人种，那么人群分层（population stratification)会成为孟德尔随机分析的混杂因素。还有一个比较常见的缺陷就是基因的多向性很难完全检测到。

随着时间的推移，孟德尔随机化研究在方法学上有了更多的发展和衍生，Smith在2014年的一篇综述中总结了这些衍生方法，如two sample Mendelian randomization，bidirectional and network Mendelian randomization，Hypothesis-free Mendelian randomization和新英格兰这篇文章应用到的Factorial Mendelian randomization。感兴趣的伙伴，不如从新英格兰的这篇文章入手，去了解孟德尔随机化的基本原理和高阶应用。

参考文献：