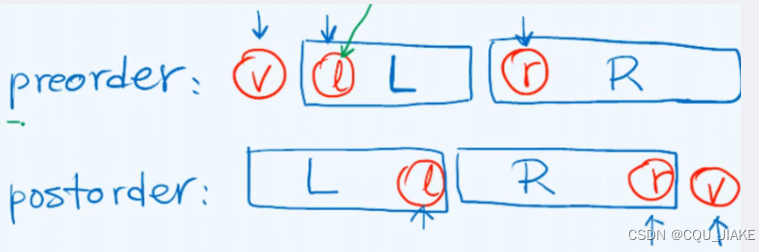
如果left<=right，就表明其之间还有元素，即左右指针重合，区间只有一个元素也被包含其中；
left<right,就表明递归过程中，只允许区间有两个及以上的元素，不允许区间只有一个元素，那么对应地，当递归终止时，即left=right,恰好指向同一个元素
二分
int arr[100];
int search(int key, int begin, int end) {if (begin > end) {return -1;}int left = begin, right = end, mid = (left + right) >> 1;while (left <= right) {if(arr[mid]==key){return mid;}else if (arr[mid] < key) {left = mid + 1;}else {right = mid - 1;}mid = (left + right) >> 1;}return -1;
}二叉查找树
ACD
重构二叉查找树，只需要除了中序遍历以外的其他任意一种遍历序列即可；因为二叉查找树的中序遍历是有序序列，所以只需要对前序序列或后序序列排序，即可得到该二叉树对应的中序序列，然后就是已知前序中序，已知后序中序重构二叉树
C
需要注意，前序序列的最后一个元素不一定是最大的，但一定是最后一个根节点的孩子节点，可能是左孩子，也可能是右孩子，也就是说，可能比最后的根节点大，也可能比最后的根节点小
中序遍历结果为有序时，就说明二叉树为二叉查找树。充分必要条件
左子树所有节点的值均小于根节点的值；右子树所有节点值均大于根节点值
查找
递归
非递归
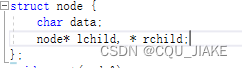
struct node {int data;node* lchild, * rchild;
};
node* search(node* bst, int key) {if (bst == nullptr || bst->data == key) {return bst;}else if (key < bst->data) {return search(bst->lchild, key);}else {return search(bst->rchild, key);}
}
node* search1(node* bst, int key) {node* ptr = bst;while (ptr != nullptr && ptr->data != key) {if (key < ptr->data) {ptr = ptr->lchild;}else {ptr = ptr->rchild;}}return ptr;
}插入，只在没找到时进行
插入的步骤，首先是要让当前节点变空，根据特定的方式找到相对应的应该是空的节点；
然后就是要让当前数据作为该节点的数据值，即把空结点变为非空结点
node* insert(node* bst, int key) {if (bst == nullptr) {bst = new node(key);}else if (key < bst->data) {bst->lchild = insert(bst->lchild, key);}else {bst->rchild = insert(bst->rchild, key);}return bst;
}非递归
node* insert1(node* bst, int key) {node* father = nullptr;node* cur = bst;while (cur != nullptr && cur->data != key) {father = cur;if (key < cur->data) {cur = cur->lchild;}else {cur = cur->rchild;}}//找到对应的空节点if (cur == nullptr) {//,如果结束后节点不为空，就说明该数据在该二叉树上，就不进行插入cur = new node(key);if (father == nullptr) {bst = cur;}else if (key < father->data) {father->lchild = cur;}else {father->rchild = cur;}}return bst;
}
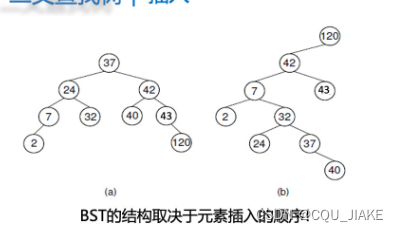
BST的结构取决于元素插入的顺序
删除
分几种情况，删除节点为叶子节点，只有一个孩子节点或只有单一方向的节点，既有左子节点又有右子节点
就是中序序列中，该节点的相邻两节点
删除
node* remove(node* bst, int key) {node* cur = bst;node* father = nullptr;while (cur != nullptr && cur->data != key) {father = cur;if (key < cur->data) {cur = cur->lchild;}else {cur = cur->rchild;}}//先找到对应的要删除的节点if (cur == nullptr) {//没找到，就说明不在树上，就不删除return bst;}//前驱节点，father有什么用？if (cur->lchild && cur->rchild) {node* tmp = cur;father = cur;cur = cur->rchild;while (cur->lchild != nullptr) {father = cur;cur = cur->lchild;}tmp->data = cur->data;}
}
3.做后序遍历
遍历二叉树，层序遍历
struct node {int data;node* lchild, * rchild;node(int x) :data(x), lchild(nullptr), rchild(nullptr) {}
};
void pre(node* root) {if (root == nullptr) {return;}cout << root->data;pre(root->lchild);pre(root->rchild);
}
void in(node* root) {if (root == nullptr) {return;}in(root->lchild);cout << root->data;in(root->rchild);
}层序遍历
void levelorder(node* root) {if (root == nullptr) {return;}queue<node*>q;q.push(root);while (!q.empty()) {node* cur = q.front();q.pop();cout << cur->data << " ";if (cur->lchild) {q.push(cur->lchild);}if (cur->rchild) {q.push(cur->rchild);}}
}struct node {int data;node* lchild, * rchild;node(int x) :data(x), lchild(nullptr), rchild(nullptr) {}
};void level(node* root) {if (root == nullptr) {return;}queue<node*>q;q.push(root);while (!q.empty()) {node* cur = q.front();q.pop();cout << cur->data << " ";if (cur->lchild) {q.push(cur->lchild);}if (cur->rchild) {q.push(cur->rchild);}}
}注意事项
入队元素不是二叉树结点的数据域，是整个二叉树节点
那么在改变队列元素类型的时候：
要求队列元素为二叉树节点类型的指针，来接收节点地址
层序遍历应用，检测是不是完全二叉树
思路就是层序遍历树，一旦遇到空结点，那么就退出；
如果是完全二叉树的话，那么这个空结点就是末尾，即已经遍历完了整棵树，
如果不是完全二叉树，就说明还有空缺，还有没遍历到的节点，也就是说队列里还有数据
bool complete(node* root) {if (root == nullptr) {return true;}queue<node*>q;q.push(root);while (!q.empty()) {node* cur = q.front();q.pop();if (cur == nullptr) {break;}//此时判断是不是完全二叉树，就需要左右子树都加入队列当中//如果是完全二叉树，就不会先遇到空结点，遇到就是最后的节点q.push(cur->lchild);q.push(cur->rchild);}if (q.empty()) {return true;}else {return false;}
}根据遍历序列重构二叉树
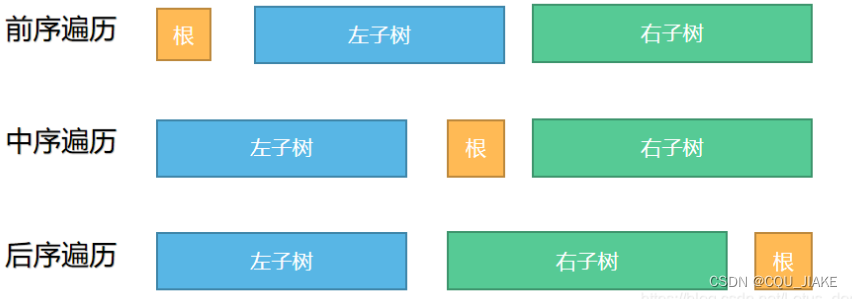
前序+中序
先根据前序遍历找到根节点，在中序序列中找到根节点的位置，然后就可以在中序序列中区分出左子树与右子树。然后就得到左子树的节点数量，即中序序列中根节点下标减去此时中序序列的起点。那么对应右子树的节点数量就是根节点的下一个下标一直到中序序列结尾。
在说构建左子树时，前序遍历里左子树里的第一个就是左子树的根节点，而由于上层递归划分出了左子树的区域，即该区域里都是左子树里的节点，那么也就相当于是在左子树的区域里构建一个树，实际上也就是重复建树这一过程，即将建树的问题划分为了了两个相同的子问题
构建要返回，返回的就是树的根节点。每层递归，只构建一个节点，就是前序的根节点
怎么导入树的遍历序列？
用char*,有一个好处是可以直接截取相应的数组，只需要对数组名做修改就可以，就类似于sort函数里的。
int nfind(char* inorder, int size, char v) {for (int i = 0; i < size; i++) {if (inorder[i] == v) {return i;}}//在中序序列中找到树根的位置，找的值就是当时截取的前序序列里的第一个元素
}
node* build(char* preorder, char* inorder, int size) {//前两个参数都是该子树的区域的起点，只是起点，数组名就代表是开始的起点，第一个元素if (!size) {//然后size就代表是这个子树里的节点个数，前序与中序里的数量是一定一致的return nullptr;}char rd = preorder[0];//由于传入的是数组名，所以第一个元素就代表的是截取的数组里的第一个元素//即传入的数组和原来的大数组已经不是同一个数组了，是截取后的数组，所以可以直接取第一个元素，就是树根int leftsize = nfind(inorder, size, rd);node* root = new node(rd);//中序为左根右，先序为根左右，根已经构建了，所以中序依然不变（指数组头元素，即左子树里第一个元素依然在中序序列的头元素里），root->lchild = build(preorder + 1, inorder, leftsize);//变的是大小，size->leftsize，以及先序序列的头元素，由于是跟左右，所以往后一个就是左子树的序列，而且第一个元素就是左子树里的根节点root->rchild = build(preorder + 1 + leftsize, inorder + 1 + leftsize, size - 1 - leftsize);//先序序列里要越过左子树区域与根节点，中序序列里要越过左子树与根节点，所以加的数据都是一样的return root;
}//需要注意，右子树大小为size-1-leftsize,因为size包含了根节点，即由根节点，左子树区域，右子树区域构成，根节点已经构建了，所以也要被刨掉，所以多个-1，而不是区间长度的问题后序+中序
后序是左右根，先根据后序序列找到根节点，以此找到根节点在中序序列中位置，以此在中序序列中划分出左右子树，在左右子树中，后序序列的最后一个元素都是其子树的根节点，能构建一层，就能递归向下构建出全部
int nfind(char* inorder, int size, char v) {for (int i = 0; i < size; i++) {//i就是要从0开始，因为是char*,传入的时候是被截取的数组，不是原来的长数组if (inorder[i] == v) {return i;}}return -1;
}
node* build(char* pastorder, char* inorder, int size) {if (!size) {return nullptr;}char rd = pastorder[size - 1];node* root =new node(rd);int leftsize = nfind(inorder, size, rd);//后序是左右根，所以在构建左子树时，左孩子的数组开头是不用动的，在右子树时，后序只需要越过左子树区域，即leftsize即可，而不需要根节点//在中序中是左根右，所以还需要越过1个根节点.右子树大小和之前一样，依然要减去左子树大小以及一个根节点大小root->lchild = build(pastorder, inorder, leftsize);root->rchild = build(pastorder + leftsize, inorder + 1 + leftsize, size - leftsize - 1);//后序是左右根return root;
}前序+后序
通过先序中的第二个元素可以找到左子树的根节点，然后在后序中找这个节点，可以确定出左子树的大小，进而可以划分出左子树与右子树
先序+后序可以重建真二叉树的原因：
通过先序序列中的第二个元素可以找到左子树的根结点并且可以求出左子树的长度从而可以找到先序序列和后序序列中的左子树序列，然后递归调用，用整体长度减去左子树长度就可以求出右子树长度从而可以找到先序序列和后序序列中的右子树序列，然后递归调用，直到退化为长度为1的情况，并将其赋值，左右子树设置为NULL，返回根结点，重建二叉树完成
但是只能构建出真二叉树，即不能有度为1的节点
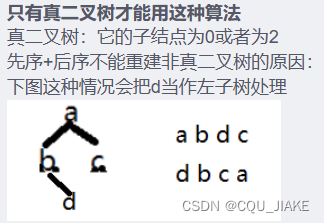当作左子树处理就是说d是b的孩子，但是是左孩子还是右孩子不能确定
int nfind(char* order, int size, char v) {for (int i = 0; i < size; i++) {if (order[i] == v) {return i;}}return -1;
}
node* build(char* preorder, char* postorder, int size) {if (!size) {return nullptr;}char rd = preorder[0];node* root = new node(rd);int leftsize = nfind(postorder, size, preorder[1]);//先序序列的第二个元素就是此时左子树的根节点，在后序序列中找到，就可以确定其左子树大小root->lchild = build(preorder + 1, postorder, leftsize);root->rchild = build(preorder + 1 + leftsize, postorder + leftsize, size - 1 - leftsize);return root;
}层序遍历
void level(node*& t) {queue<node*>q;int x;cin >> x;if (x != 0) {node* t = new node(x);q.push(t);}while (!q.empty()) {node* cur = q.front();q.pop();cin >> x;if (x != 0) {cur->lchild = new node(x);q.push(cur->lchild);}cin >> x;if (x != 0) {cur->rchild = new node(x);q.push(cur->rchild);}}
}char*数组怎么输入并传入
建树指针细节
这里传入的是一个节点指针的引用，所以在其中做修改后，可以切实修改唯一的树
这里之所以传入的是指针的引用是因为，这个树指针的节点是在上面，之前已经建立好的，这里是在对已经建好的头结点做修改
而之前没有传入，上面的话，是直接在函数里建立的新的节点，无所谓幅不副本，因为最后传出来的就是一个已经建立好的树，而之前的话，是要对原树，已经建立好的树节点做修改，所以是要传入指针的引用
所以这个传入引用的函数，是不需要返回值的，void型即可；而不需要传入引用的函数，则需要返回值为节点指针型
new后返回的就是对应数据的指针类型，new BITNODE,就会返回节点的指针
这里必须要写tree=new binode,即必须要建立一个新节点，在这里，即使最开始的树根是在外面定义好的（题目里的要求，固定格式），也必须要再定义一遍，因为在建树过程中会多次调用creat,一开始的树根有分配空间，但是它的左右孩子都没有明确分配空间，也就是都是空指针，没有明确指向某一区域，所以就需要在每个creat的过程里对传入的根节点进行new一下，分配一个空间，才能保证左右孩子指针确实是指向某一区域，而不是纯粹的空指针
结构体定义，typedef
有了typedef才能给结构体struct起别名
如果不写typedef就在后面起别名，比如*tree之类的就会报错，但如果一旦写了，就可以自由起别名，在结构体的最后，加*就是指针，不加*就是同一结构体的别名
先序输入，构建树
*只是表明数据类型，实际名字上并不加*，加*就表明在定义时定义其为指针
比如node*lchild,node*rchild,在调用时，就是root->lchild,而不是root->*lchild;
这之中，*BiTree就代表说是节点BItnODE的指针，*BITREE就是BITNODE的指针。
那么再调用的时候，只用说明BITREE即可
实际上是在定义的时候，就是在名称前加的，node*lchild就表明lchild是Node的*，指针，而不是*lchild
void creat(tree& root) {char t;cin >> t;if (t == '#') {root = nullptr;}else {root = new node;root->data = t;creat(root->lchild);creat(root->rchild);}
}
void pre(tree root) {if (!root) { return; }cout << root->data;pre(root->lchild);pre(root->rchild);
}
int main() {tree root = new node;creat(root);pre(root);return 0;
}
