💓博主CSDN主页:杭电码农-NEO💓
⏩专栏分类:C++从入门到精通⏪
🚚代码仓库:NEO的学习日记🚚
🌹关注我🫵带你学习C++
🔝🔝

哈希的应用
- 1. 前言
- 2. 位图的概念以及定义
- 3. 位图的模拟实现
- 4. 布隆过滤器的概念以及定义
- 5. 布隆过滤器模拟实现(一)
- 6. 布隆过滤器模拟实现(二)
- 7. 处理海量数据的面试题
- 8. 总结
1. 前言
哈希最常用的应用是unordered
系列的容器,但是当面对海量数据
如100亿个数据中找有没有100这
个数时,使用无序容器的话内存放不下
所以哈希思想还有别的更重要的应用!
本章重点:
本篇文章着重讲解哈希的应用的
两个容器,一个是位图,一个是布隆
过滤器,并且模拟实现它们.最后会
讲解如何使用这两个容器来解决一
些海量数据的面试题问题
2. 位图的概念以及定义
请先看一道海量数据的面试题:
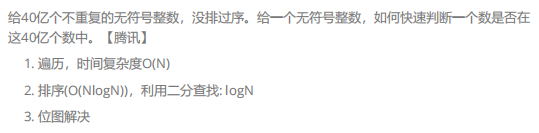
如果要使用unordered_set来解决
40亿个整数,一个整数占4四节,
总共大约占16个G的内存空间
并且set容器中不止有整型数据,还有
其他的数据,所以不能用set!
而一个数在或不在可以用1/0来表示
也就是说其实只需要一个比特位就可
以知道一个数在不在其中.
于是位图横空出世!
位图概念:
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的
举例说明:
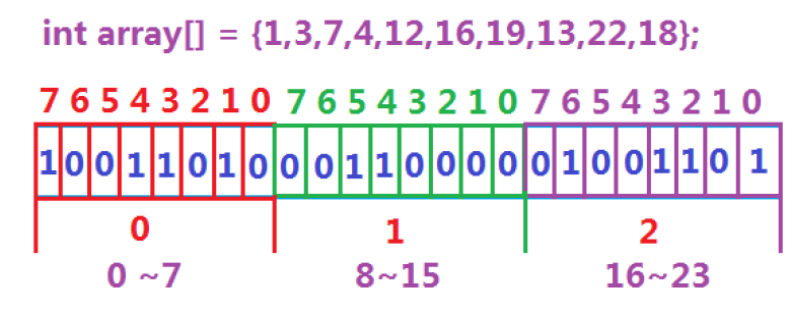
判断1~22中哪些数据是存在的
只需要用三个整型也就是24个
比特位的空间,同理,40亿个数据
也用不着16G的内存,使用0.5G
内存的位图即可判断一个数在不在!
3. 位图的模拟实现
先来看看库中实现的位图:

模板参数N代表位图的大小
位图有三个主要的接口函数:
set:将一个数据放入位图中reset:将一个数据从位图中删掉test:检测一个数据在不在位图中
位图本身就是一段连续的空间
所以用char类型数组来充当位图的
基本结构是很符合情况的!
先将位图框架写出来:
template<size_t N>//N是所有数中的最大值
class bit_set
{
public:bit_set(){_bit.resize(N / 8 + 1, 0);}void set(size_t x)//将第x位变成1{}void reset(size_t x)//将第x位由1变0{}bool test(size_t x){}
private:vector<char> _bit;
};
在写set,reset等函数时,要先清除一点,
那就是char类型的数组一个元素有八个
比特位,所以我们需要确定两个位置:
一是此数据在哪一个数组元素中
二是此数据对应此元素的第几个比特位
下面我们画个图来推导一下公式:
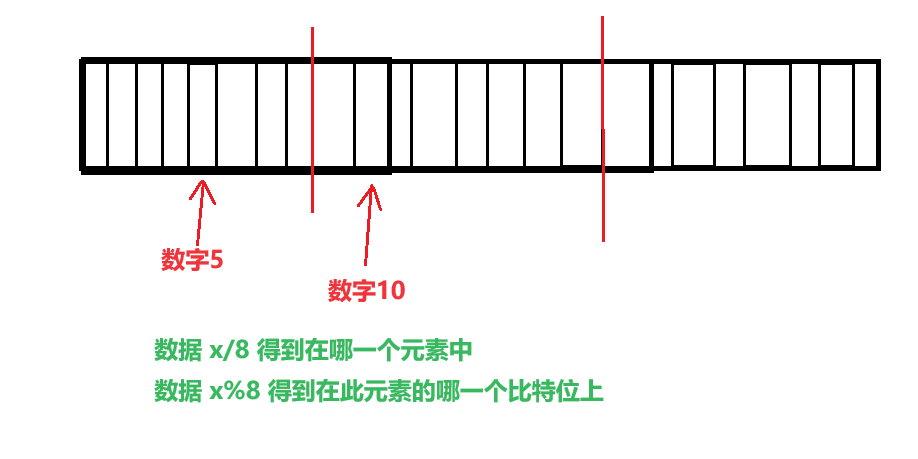
现在已经能准确的找到这个比特位了
那么怎样将这个比特位变成0/1并且
不会影响到其他的比特位呢?下面分享
两个很巧妙的方法,请大家细细品尝:
template<size_t N>//N是所有数中的最大值
class bit_set
{
public:bit_set(){_bit.resize(N / 8 + 1, 0);}void set(size_t x)//将第x位变成1{//x/8->在第几个char//x%8->在这个char的第几个比特位size_t i = x / 8;size_t j = x % 8;_bit[i] |= (1 << j);//将x对应的比特位变成1}void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bit[i] &= ~(1 << j);//将x对应的比特位变成0}bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bit[i] & (1 << j);}
private:vector<char> _bit;
};
关于代码的解释都在注释中,请耐心观看
必要时可以自己画图做做试验
4. 布隆过滤器的概念以及定义
位图有一个缺陷,那就是只能判断整型是否存在
遇见字符串等类型的数据就很难处理了
布隆过滤器的提出:

布隆过滤器的概念:
布隆过滤器是由布隆在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间
举例说明:
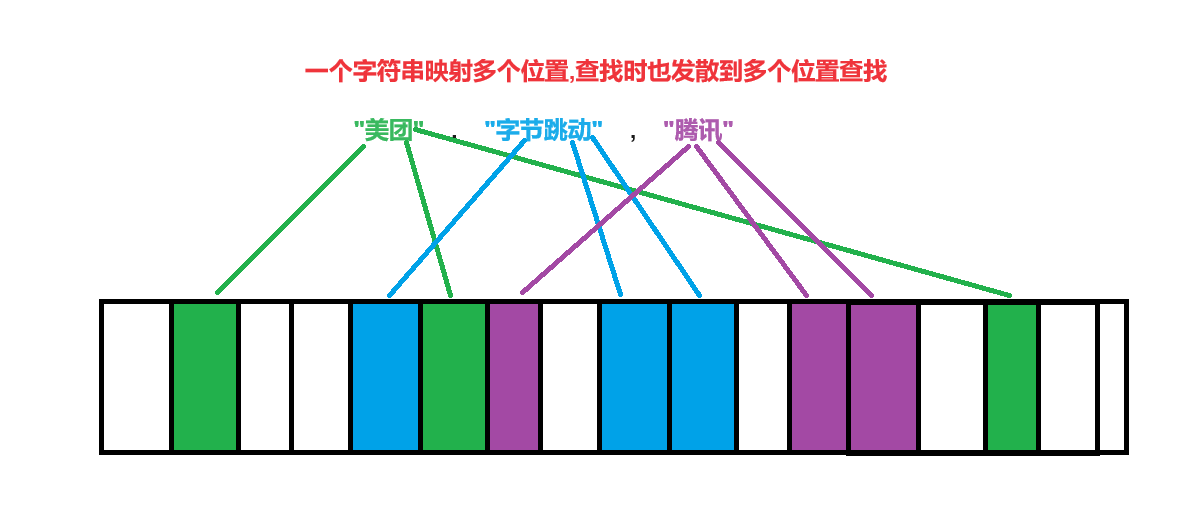
查找字符"美团"是否存在时,会找到
这三个绿色的位置,看看是否都为1
布隆过滤器的拓展阅读:
布隆过滤器原理
5. 布隆过滤器模拟实现(一)
首先,布隆过滤器的底层也是位图,所以
只需封装一层即可实现一个布隆过滤器!
但实现布隆过滤器的关键有以下几个
一个字符串映射几个位置?怎样把字符串转换为整数?一般而言,一个字符串映射的越多,那么
误判率就越低,但是映射过多会导致不同
的字符串映射到相同的位置,所以一般映射
三个位置,并且将字符串转换为整数也就
需要三种不同的方法,我在网上找了一些
字符串转整数的算法,请看下面的代码:
//三个不同的字符串映射成整数的函数
struct HashBKDR
{size_t operator()(const string& key){size_t val = 0;for (auto ch : key){val *= 131;val += ch;}return val;}
};
struct HashAP
{size_t operator()(const string& key){size_t hash = 0;for (size_t i = 0; i < key.size(); i++){if ((i & 1) == 0)hash ^= ((hash << 7) ^ key[i] ^ (hash >> 3));elsehash ^= (~((hash << 11) ^ key[i] ^ (hash >> 5)));}return hash;}
};
struct HashDJB
{size_t operator()(const string& key){size_t hash = 5381;for (auto ch : key)hash += (hash << 5) + ch;return hash;}
};
将这三个仿函数传入类,用于字符串转整型
布隆过滤器的实现:
// N表示准备要映射N个值
template<size_t N,class K = string, class Hash1 = HashBKDR, class Hash2 = HashAP, class Hash3 = HashDJB>
class Bloom_Filter
{
public:void set(const K& key){size_t hash1 = Hash1()(key) % (_ratio * N);_bits->set(hash1);size_t hash2 = Hash2()(key) % (_ratio * N);_bits->set(hash2);size_t hash3 = Hash3()(key) % (_ratio * N);_bits->set(hash3);}bool test(const K& key){size_t hash1 = Hash1()(key) % (_ratio * N);if (!_bits->test(hash1))return false; // 准确的size_t hash2 = Hash2()(key) % (_ratio * N);if (!_bits->test(hash2))return false; // 准确的size_t hash3 = Hash3()(key) % (_ratio * N);if (!_bits->test(hash3))return false; // 准确的return true; // 可能存在误判}void reset(const K& key)//支持删除操作的话,可能会把其他数据对应的映射值删除{}
private:const static size_t _ratio = 5;//开的空间越大,误判率越小std::bitset<_ratio* N>* _bits = new std::bitset<_ratio * N>;//标准库中的位图是在栈上开辟的静态数组,过大会栈溢出
};
6. 布隆过滤器模拟实现(二)
布隆过滤器的查找是一个很玄幻的过程:
分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零,代表该元素
一定不在哈希表中,否则可能在哈希表中
因为哈希函数可能存在冲突的原因,如下:
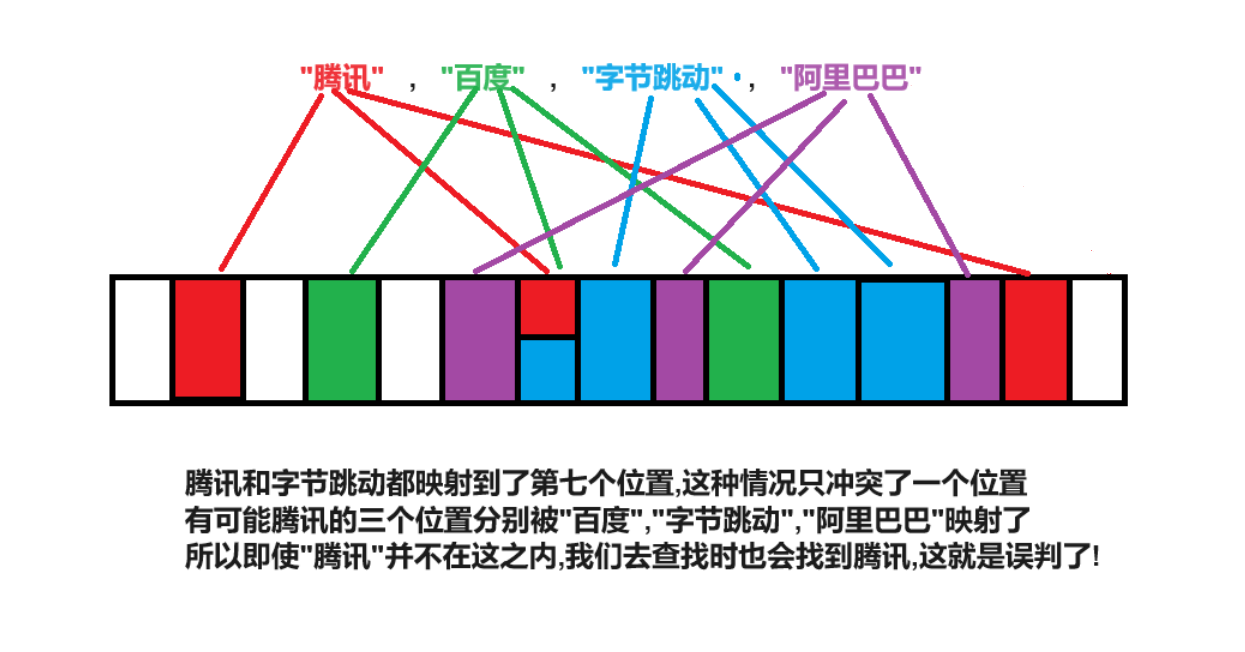
所以我们得出一个结论:
布隆过滤器说一个元素存在,那它可能存在布隆过滤器说一个元素不在,那它一定不在
布隆过滤器的删除操作:
如果你理解了上面的内容,你一定能
明白布隆过滤器是不支持删除的,因为
删除一个关键字时可能将其他的关键字
的一部分也给删除了,因为一个bit位
只能存储一个二进制信息!

7. 处理海量数据的面试题
海量数据的处理,有对位图的应用
也有对布隆过滤器的应用一步一步解析
位图的应用:
- 给100亿个整数,设法找到只出现一次的整数?
- 给两个文件,分别有100亿个整数,只有1G内存,如何找到两个文件交集?
- 位图应用变形:一个文件有100亿个int,1G内存,设法找到出现次数不超过2次的所有整数
布隆过滤器的应用:
- 给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
- 如何扩展BloomFilter使得它支持删除元素的操作
这些问题大家可以下来想一想,有什么问题欢迎私信
8. 总结
讲到这里,哈希的所有内容就已经
讲完了,所以无脑哈希无脑哈希,
但实际上要学好哈希还真得费点脑子
海量数据得处理问题在面试时也是
经常问的,希望同学们好好学扎实!






![[个人笔记] vCenter6.7使用自建SSL证书](https://img-blog.csdnimg.cn/38b6d31ece0347c8a15dfb79369f8556.png)