Matlab通信仿真系列——随机信号分析

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等
在这里插入图片描述
本节目录

一、平稳随机过程
1、相关函数和功率谱密度
2、Matlab频谱图绘制
二、带通随机过程
1、定义以及Matlab实现与绘制
三、随机过程通过线性系统
1、定义
2、Matlab实现与绘制
四、Matlab源码
1、平稳随机过程源码
2、带通随机过程源码
3、随机过程通过线性系统源码

本节内容
信号分为确定性信号和随机信号，通信过程中的随机信号和噪声均归纳为依赖于时间参数t的随机过程。它是时间t的函数，但在任意时刻上观察到的值是不确定的，是一个随机变量。
一、平稳随机过程
1、相关函数和功率谱密度
平稳随机过程，它的任何n维分布函数或概率密度函数与时间起点无关。
随机过程X(t)在任意一组时刻t1＞t2＞t3…＞tn且n为任意值时得到的随机变量Xti,i=1,2,3,…n的联合概率密度函数满足：
P(x(t1),x(t2),x(t3)…,x(tn))
=P(x(t1+t),x(t2+t),x(t3+t)…,x(tn+t))
严平稳过程，对所有t和n都成立，t是任意时刻。
宽平稳过程，平稳随机过程的数学期望及方差与t无关，自相关函数只与时间间隔τ有关，R(t1,t1+τ)=R(τ)
平稳随机过程的功率谱密度S(f)定义为自相关函数的傅里叶变换。
一个平稳随机过程X(t)的自相关函数可以有功率谱密度的傅里叶逆变换得到。
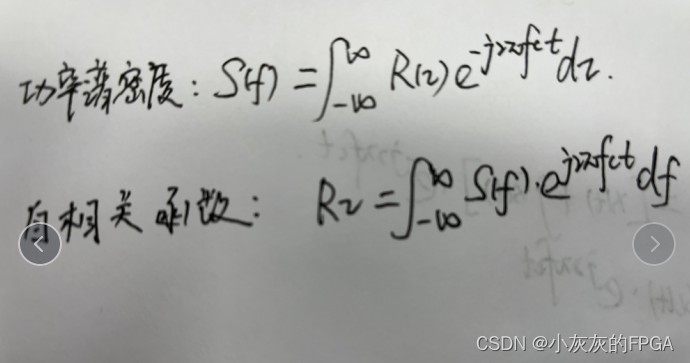
在这里插入图片描述

正态随机过程，又称为高斯过程，在通信信道中的噪声，通常是一种正态随机过程。正态随机过程的n维分布仅由各随机变量的数学期望、方差和两两之间的归一化协方差函数决定。
当然，对通信系统的热噪声进行建模时候，通常假设这样的噪声是白色高斯随机过程，即功率谱密度S(f)对所有的f是一个常数。热噪声的功率谱密度和自相关函数
在这里插入图片描述

其中δ(τ)为单位冲激函数。当τ≠0时，R(τ)=0。
对一个白色高斯随机过程中任意两个时间点上进行采样，所得到的随机变量一定是不相关的，也就是统计独立的高斯随机变量。
2、Matlab实现与绘制

matlab代码示例：
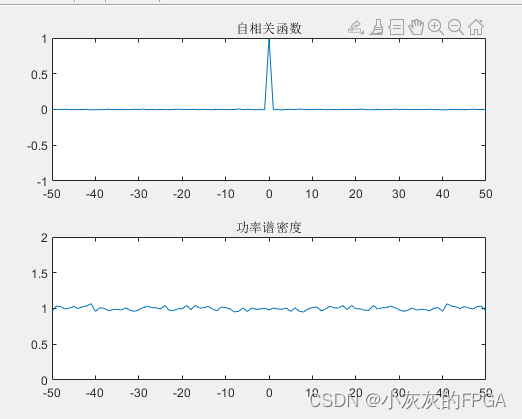
产生100个N=2000的独立分布的均值为0，
方差为1的高斯分布随机离散时间序列，
并计算自相关估值和功率谱密度的平均值。

在这里插入图片描述

r = xcorr(x,y)
xcorr - 互相关

此 MATLAB 函数返回两个离散时间序列的互相关。
互相关测量向量 x 和移位（滞后）副本向量y 的之间的相似性，形式为滞后的函数。如果 x 和 y 的长度不同，函数会在较短向量的末尾添加零，使其长度与另一个向量相同。

二、带通随机过程
1、定义以及Matlab实现与绘制
若随机过程的功率谱在某中心频率±f0附加的一个频段内有值，而在频率之外功率谱密度为0，称这个随机过程是带通过程，若通带B<<f0，称为一个窄带过程。

matlab代码示例：
一个噪声的自相关函数为R(τ)=sinc(2Bτ)cos(2πf0τ),
其中B=20,fc=100,求该随机过程的功率谱密度。

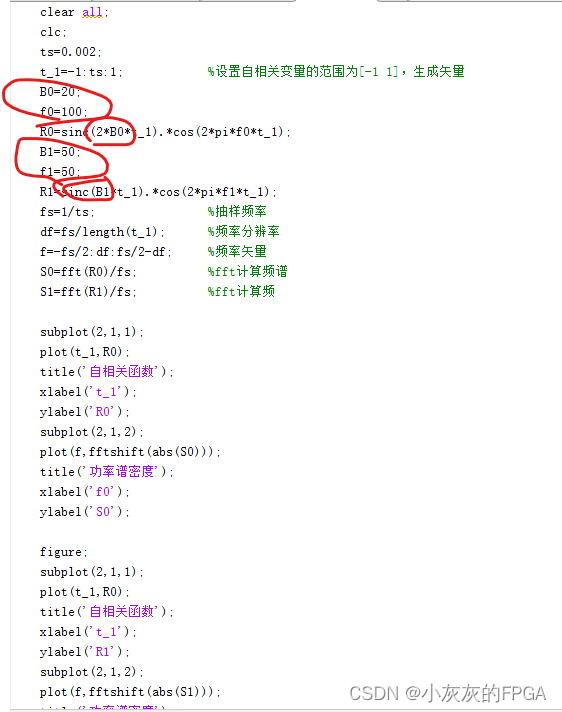
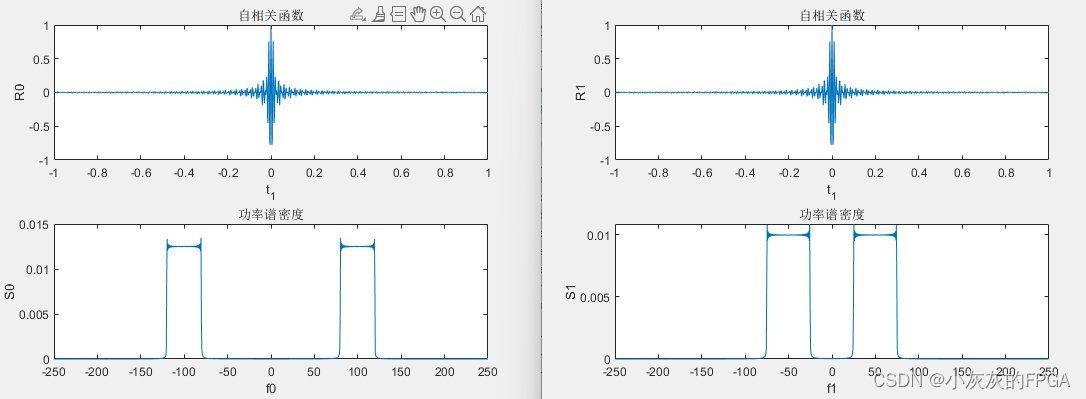
在这里插入图片描述

左图随机过程的中心频率在±100Hz，带宽40dB范围内；
左图随机过程的中心频率在±50Hz，带宽50dB范围内；
三、随机过程通过线性系统
1、定义
一个平稳随机过程X(t)通过某个线性时不变滤波器h(t)，该滤波器的输出Y(t)是随机过程。
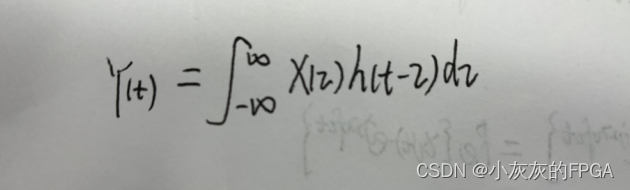
在这里插入图片描述

输出过程Y(t)的功率谱密度与输入过程X(t)的功率谱密度以及线性滤波器的频率响应关系式
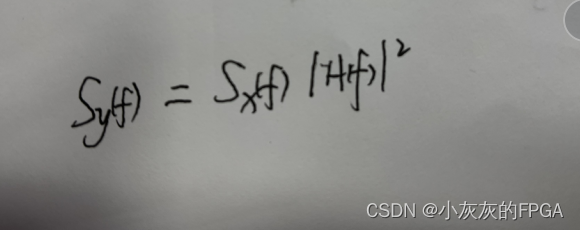
在这里插入图片描述

2、Matlab实现与绘制

matlab代码示例：
白噪声输入序列Xn,均值为0，
方差为1的高斯分布随机变量组成，
通过一个滤波器产生的序列，滤波器的脉冲响应为：

在这里插入图片描述

四、Matlab源码
1、平稳随机过程源码

clear all;
clc;
%产生100行2000列的高斯分布随机数
%均值为0，方差为1，每一行代表一个离散时间序列
N1=2000;
N2=100;
x=randn(N2,N1);  
%计算每一行的自相关函数估值和频率谱密度估值
%xcorr计算自相关值的函数
%lags自相关系数的延迟时间，50
%coeff,归一化自相关系数
for ii=1:N2[Rx(ii,:),lags]=xcorr(x(ii,:),50,'coeff');Sf(ii,:)=fftshift(abs(fft(Rx(ii,:))));
end
Rx_av=sum(Rx)/N2;       %自相关估值平均
Sf_av=sum(Sf)/N2;       %功率谱密度估值平均
subplot(2,1,1);
plot(lags,Rx_av);
title('自相关函数');
axis([-50 50 -1 1])     %axis - 设置坐标轴范围和纵横比,y[-50 50],x[-1 1]
subplot(2,1,2);
plot(lags,Sf_av);
title('功率谱密度');
axis([-50 50 0 2])      %axis - 设置坐标轴范围和纵横比,y[-50 50],x[0 2]

2、带通随机过程源码

clear all;
clc;
ts=0.002;
t_1=-1:ts:1;            %设置自相关变量的范围为[-1 1]，生成矢量
B0=20;
f0=100;
R0=sinc(2*B0*t_1).*cos(2*pi*f0*t_1);
B1=50;
f1=50;
R1=sinc(B1*t_1).*cos(2*pi*f1*t_1);
fs=1/ts;                %抽样频率
df=fs/length(t_1);      %频率分辨率
f=-fs/2:df:fs/2-df;     %频率矢量
S0=fft(R0)/fs;          %fft计算频谱
S1=fft(R1)/fs;          %fft计算频subplot(2,1,1);
plot(t_1,R0);
title('自相关函数');
xlabel('t_1');
ylabel('R0');
subplot(2,1,2);
plot(f,fftshift(abs(S0)));
title('功率谱密度');
xlabel('f0');
ylabel('S0');figure;
subplot(2,1,1);
plot(t_1,R0);
title('自相关函数');
xlabel('t_1');
ylabel('R1');
subplot(2,1,2);
plot(f,fftshift(abs(S1)));
title('功率谱密度');
xlabel('f1');
ylabel('S1');

3、随机过程通过线性系统源码

clear all;
clc;
%产生100行2000列的高斯分布随机数
%均值为0，方差为1，每一行代表一个离散时间序列
N1=2000;
N2=100;
x=randn(N2,N1);  
%计算每一行的自相关函数估值和频率谱密度估值
%xcorr计算自相关值的函数
%lags自相关系数的延迟时间，50
%coeff,归一化自相关系数
for ii=1:N2y(ii,1)=x(ii,1);for jj=2:N1y(ii,jj)=0.6*y(ii,jj-1)+x(ii,jj);end[Ry(ii,:),lags]=xcorr(y(ii,:),50,'coeff');Sf(ii,:)=fftshift(abs(fft(Ry(ii,:))));
end
Ry_av=sum(Ry)/N2;       %自相关估值平均
Sf_av=sum(Sf)/N2;       %功率谱密度估值平均
subplot(2,1,1);
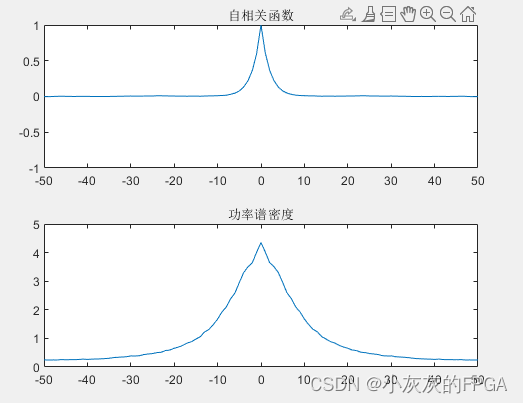
plot(lags,Ry_av);
title('自相关函数');
axis([-50 50 -1 1])     %axis - 设置坐标轴范围和纵横比,y[-50 50],x[-1 1]
subplot(2,1,2);
plot(lags,Sf_av);
title('功率谱密度');
axis([-50 50 0 5])      %axis - 设置坐标轴范围和纵横比,y[-50 50],x[0 2]