1. Push-Relabel算法思想

对于一个网络流图: 该算法直观可以这样理解，先在源节点处加入充足的流(跟源节点$s$相连的所有边的容量之和)，然后开始按一定规则进行流渗透，一个边一个边的向汇点渗透，直到没法再渗透（类似于Ford-Fulkerson算法中找不到增广路径了），那么这时再把一些剩余的流回收到源节点$s$就可。
主要分为两个步骤：push和relabel。push表示从所有节点找出一个存水量大于0的节点$u$，将它所存的水尽可能推向与它相邻的节点$v$。要实现该push的操作必须满足下面条件：该点存水量$e(u)>0$，节点$u$的高度大于节$v$的高度。本次推送的流值$(\mathbf{u},\mathbf{v}).f=\min \mathbf{e}(\mathbf{u}),(\mathbf{u},\mathbf{v}).capacity$为边 $\mathbf{edge}(\mathbf{u},\mathbf{v})$的当前容量，这个值在推进过程中会一直变换。relabel表示某一个节点存水量大于0但水流不出去时，我们对该节点高度增加1，这就是所谓relabel操作，使得该节点的存水量流入比它低的节点。一开始的时候我们设置源节点高度为$N$,此处$N$为节点数，其他所有节点高度为0，并且汇节点的高度固定为0，其他节点高度在算法执行过程中高度$h$会改变。

算法步骤：
1.初始化前置流：将与源点s相连的管道流量$f(0,i)$设为该管道的容量，即$f(0,i)=c(0,i)$；将源点$s$的高度$h(0)=V$，($V$表示图的顶点个数)，其余顶点高度$h(i)=0$；将源的点余量$e(0)$设为源容量减去源的流出量，即$e(0)=-\sum f(0,i)=-\sum c(0,i)$，与源$s$相连的点余量设为该点的流入量$e(i)=c(0,i)$，其余点都为0。

2.搜索是否有节点的点余量$e(u)>0$，如果存在，表示要对该点进行操作——重标记或者压入流：检查与该点$u$全部的相邻点$v$，若该点比它相邻点的高度大$h(u)>h(v)$,该管道的当前容量为$c(u,v)$，将该点$u$的余量以最大方式压入该管道$delta=min(e(u),c(u,v))$,然后对节点$u$,$v$的余量$e$、边$(u,v)$的容量进行相应的进行减加操作；如果找不到高度比自己低的相邻节点$v$,则对节点$u$的高度增加1，即$h(u)=h(u)+1$。如此继续进行Push操作。以上的重标记或压入流操作循环进行，直至该点的余量$e(u)$为0。

3.重复第2步，直找不到余量大于0的节点，停止算法，最后输出汇点$t$的余量$e(t)$,该值就是最后所求的最大流。最小割。

2.Push-Relabel算法原理示意图

给定的网络流图如下：

第一步：初始化操作：

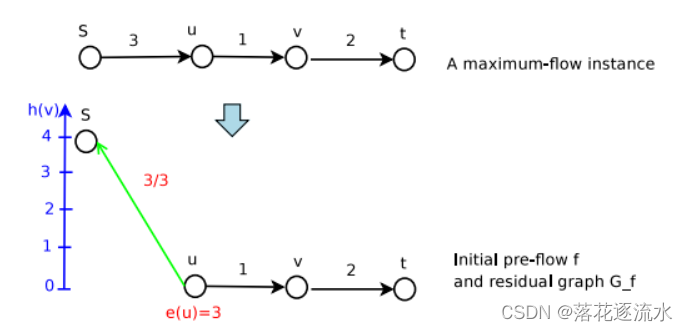
第一次Push不成功，进行Relabel

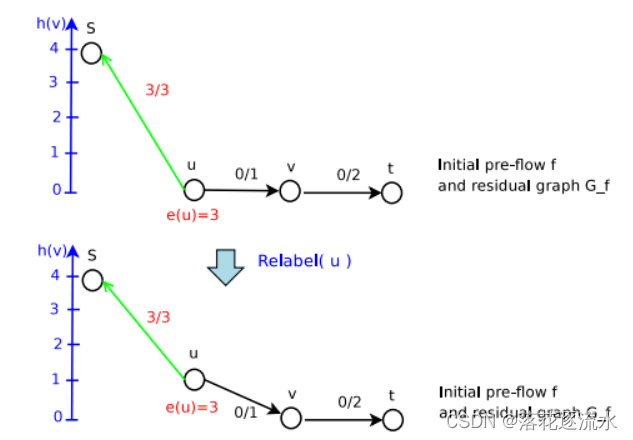
第二次Push，成功

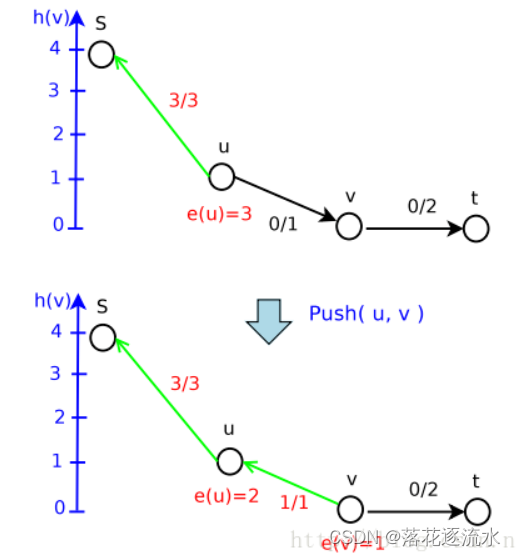
继续Push

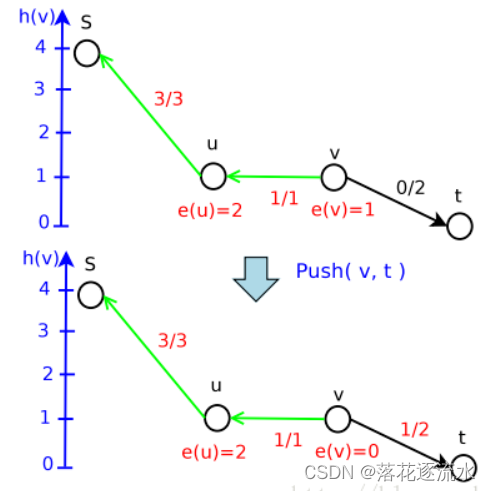
继续Push

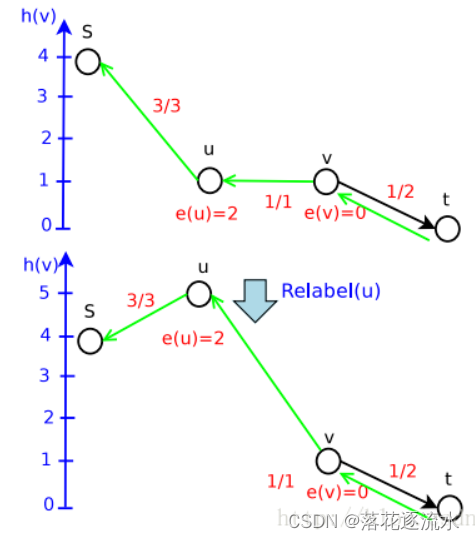
继续Push

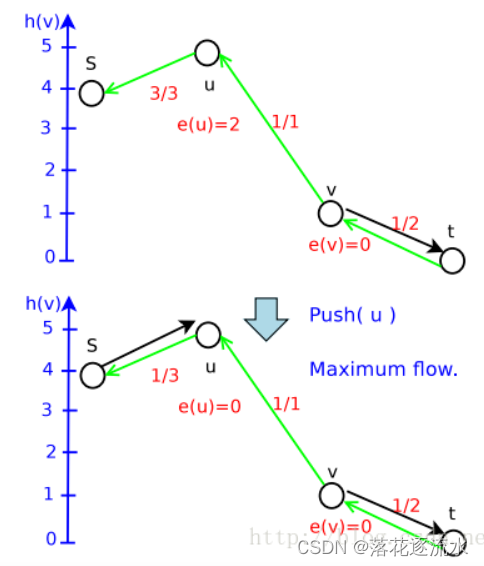
至此结束。

3.Push-Relabel算法具体实例

求解下面网络流图的最大流：

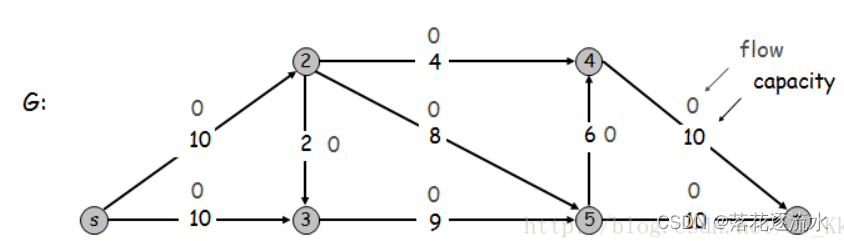
源节点为s
,汇节点为t

具体程序实现如下：

/****************************************************
Description:Push-Relabel算法求解网络最大流
Author:Robert.TY
Date:2016.12.10 
****************************************************/ 
#include<iostream>
#include<limits>
#include<iomanip> 
using namespace std;
struct Point{char ch;//节点标识 int e;//存货量int h;//高度 
};    
Point point[6];               
int graph[6][6]={{0,10,10,0,0,0},{0,0,2,8,4,0},{0,0,0,9,0,0},{0,0,0,0,9,10},{0,0,0,0,0,10},{0,0,0,0,0,0}} ;        
int Push_Relabel(int s, int t,int n); //参数为 起点  端点  节点数 int main(){  int  n=6;  point[0].ch='s';  point[0].e=0; point[0].h=0; point[1].ch='u';  point[1].e=0; point[1].h=0; point[2].ch='v';  point[2].e=0; point[2].h=0; point[3].ch='a';  point[3].e=0; point[3].h=0; point[4].ch='b';  point[4].e=0; point[4].h=0; point[5].ch='t';  point[5].e=0; point[5].h=0; cout<<"原始网络图邻接矩阵："<<endl;for(int i=0;i<=5;i++){for(int j=0;j<=5;j++){cout<<setw(6)<<graph[i][j]<<" ";}cout<<endl;} cout<<"max_flow="<<Push_Relabel(0, n-1,n)<<endl; cout<<"graph流图矩阵："<<endl;for(int i=0;i<=5;i++){for(int j=0;j<=5;j++){cout<<setw(6)<<graph[i][j]<<" ";}cout<<endl;} return 0;  
} int Push_Relabel(int s, int t,int n)  
{  int  max_flow;point[s].h = n;  //起始点高度置为n 最高//初始化 将start点的库存 流出去 update剩余图 for (int u = 1; u <= t; u++) {  if (graph[s][u] > 0) {  point[u].e = graph[s][u];  point[s].e -= graph[s][u];  graph[u][s] = graph[s][u];  graph[s][u] = 0;  }   }while(1) {  int finishflag = 1;  for (int u = s+1; u < t; u++) {  //搜索除  节点s 节点t以外的节点 if (point[u].e > 0) {  //发现库存量大于0的节点 u  进行push finishflag = 0;  int relabel = 1;   //先假设顶点u需要relabel  提高高度h for (int v = s; v <= t && point[u].e > 0; v++) {   //搜索能push的顶点   if (graph[u][v] > 0 && point[u].h >point[v].h) {  //发现节点v relabel = 0;  //顶点u不需要relabelint bottleneck = min(graph[u][v], point[u].e);  point[u].e -= bottleneck; //u节点库存量减少 point[v].e += bottleneck; //v节点库存量减少graph[u][v] -= bottleneck;  graph[v][u] += bottleneck;  }  }  if (relabel==1) {  //没有可以push的顶点,u节点需要relabel 提高高度point[u].h += 1;   }  }  }  if (finishflag==1) { // 除源点和汇点外,每个顶点的e[i]都为0 max_flow = 0;  for (int u = s; u <= t; u++) {  if (graph[t][u] > 0) {  max_flow += graph[t][u];  }  }  //cout<<"max_flow="<<max_flow<<endl;break;  }  }  return max_flow;  
}  

结果如下：

原始网络图邻接矩阵：0     10     10      0      0      00      0      2      8      4      00      0      0      9      0      00      0      0      0      9     100      0      0      0      0     100      0      0      0      0      0
max_flow = 19
graph 流图矩阵：0      0      1      0      0      010      0      2      2      0      09      0      0      0      0      00      6      9      0      4      00      4      0      5      0      10      0      0     10      9      0--------------------------------
Process exited after 0.04971 seconds with return value 0Press ANY key to exit...

最大流可以通过最后一行的数值得到，即与t直接相关联的流量。

参考：最大流网络之Push-Relabel算法

4. push relabel与图割

Push-relabel算法是一种用于求解最大流问题的算法，也可以应用于图像分割领域。下面是将Push-relabel算法应用于图像分割的基本步骤：

构建图：首先，将输入图像转换为图的形式。每个像素被表示为一个节点，每个相邻的像素之间存在一条边，边的权重可以表示像素之间的差异或相似度。
初始化：对图进行初始化，通常将每个节点的标签初始化为一个唯一的整数。
推送流：从源节点开始，通过不断地推送流和重新标签化的操作，将流从源节点推送到汇节点。在这个过程中，Push-relabel算法会尝试将更多的流推送到已经饱和的节点，直到无法再推送更多的流为止。
重新标签：在推送流的过程中，当一个节点接收到的流超过其容量时，该节点会变得“饱和”。Push-relabel算法会为这个节点分配一个新的标签，并将这个节点与新标签之间的边进行更新。
更新残量网络：在推送流和重新标签的过程中，Push-relabel算法会不断更新残量网络，即还没有被推送到的边的集合。
判断终止条件：如果无法再找到新的增广路径（即无法再推送更多的流），则算法终止。
后处理：在得到最大流后，需要将结果映射回原始的图像。通常，可以将每个节点的标签映射为其所属的集合（即分割结果），或者将每个边的流量映射为边缘检测结果。
输出结果：最后，根据映射后的结果进行适当的后处理，如去除小面积的区域、平滑边缘等，以提高分割的质量。
通过以上步骤，可以使用Push-relabel算法进行图像分割。需要注意的是，Push-relabel算法通常会得到多解，因此需要进行合适的后处理和参数调整，以获得最佳的分割结果。

伪代码：

Push-relabel算法的伪代码如下：初始化：对于每个节点u，设置low_water_mark[u] = 0和high_water_mark[u] = INF（一个很大的数）
对于每个节点u，设置label[u] = 0和delta[u] = 0
对于每条边(u,v)，设置residual_capacity[u,v] = capacity[u,v]，residual_flow[u,v] = 0
while there is a path from source to sink in the residual graph:从源节点开始，使用DFS或BFS等搜索算法搜索增广路径
在搜索过程中，维护一个当前节点的集合C和一条从源节点到集合C的最小割
对于每个节点u，如果u不在C中且delta[u] > 0，执行push操作：
从集合C中选择一个节点v，使得(u,v)在residual_graph中且residual_capacity[u,v] > 0
将流从u推送到v，即令delta[v] = delta[v] + delta[u]，residual_flow[u,v] = residual_flow[u,v] + delta[u]，residual_capacity[u,v] = residual_capacity[u,v] - delta[u]
将low_water_mark[v]更新为low_water_mark[u] + delta[v]，high_water_mark[v]更新为high_water_mark[u] + delta[v]，label[v]更新为label[u] + delta[v]
将low_water_mark[u]更新为max(low_water_mark[u], high_water_mark[v])，high_water_mark[u]更新为max(high_water_mark[u], label[v])，label[u]更新为label[v] - delta[u]
输出结果：将每个节点的标签映射为其所属的集合（即分割结果），或者将每个边的流量映射为边缘检测结果。需要注意的是，Push-relabel算法通常会得到多解，因此需要进行合适的后处理和参数调整，以获得最佳的分割结果。

参考：
参考：
参考：
参考：
参考：