原理

奇异值分解是让机器从大量数据集中提取出关键信息的重要手段。（矩阵中的泰勒公式，哈哈）

思考：如果就矩阵的本质是线性变换而言的话，那A矩阵分解后是不是相当与先进行旋转→放缩→旋转呢？

求解奇异值的步骤：

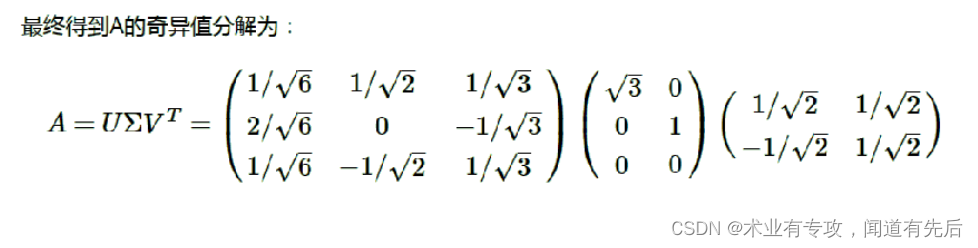
SVD的用途：

1.通过SVD对数据的处理，我们可以使用小得多的数据集来表示原始数据集，这样做实际上是
去除了噪声和冗余信息，以此达到了优化数据、提高结果的目的。
2.隐形语义索引：最早的SVD应用之一就是信息检索，我们称利用SVD的方法为隐性语义检索
（LSI）或隐形语义分析（LSA）
3.推荐系统：SVD的另一个应用就是推荐系统，较为先进的推荐系统先利用SVD从数据中构建一
个主题空间，然后再在该空间下计算相似度，以此提高推荐的效果。

注：SVD和PCA不同，PCA是对数据的协方差矩阵进行矩阵的分解，而SVD是直接在原始矩阵上进行分解

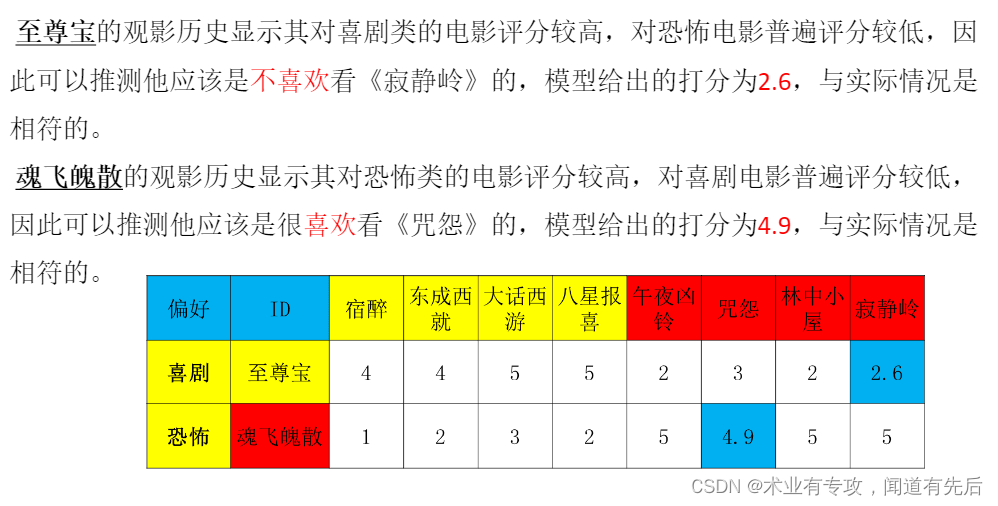
一个推荐系统：

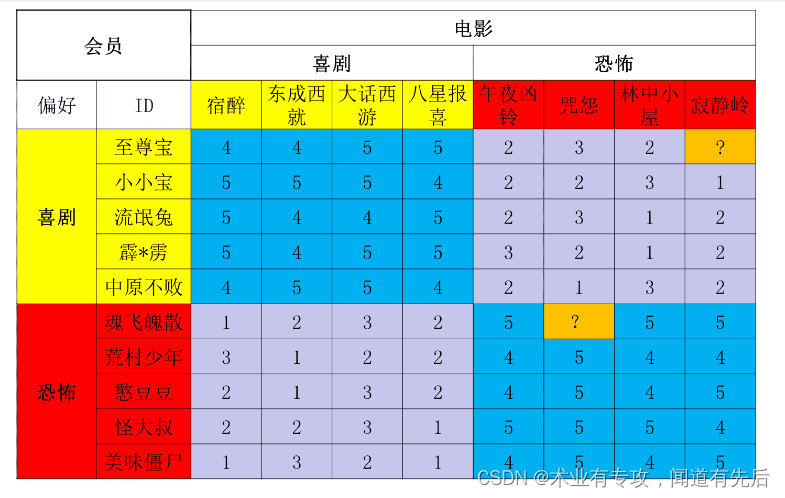
转换为矩阵，空缺值填充为0

按重要程度挑选奇异值

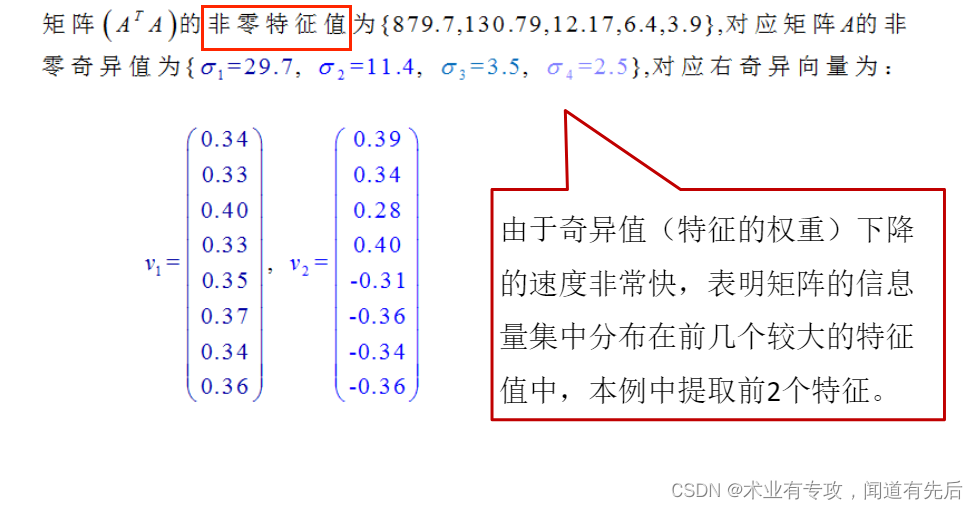
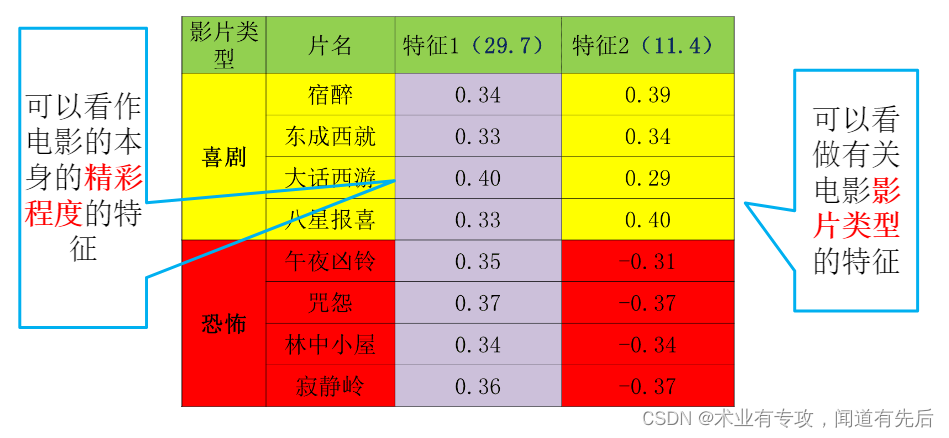
原理

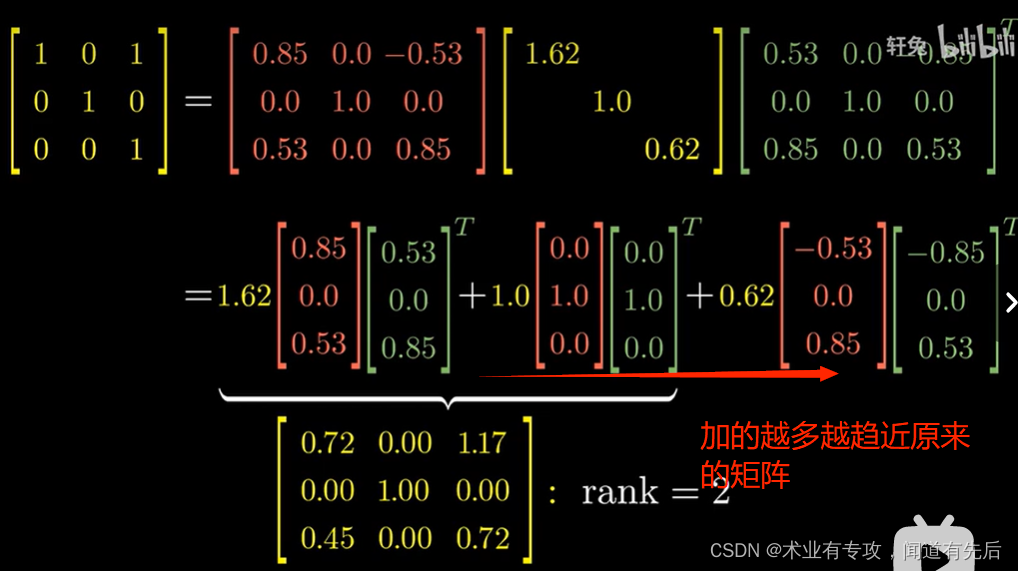
挑选重要的分解如下

计算

图像压缩技术