一、简答题

1、试述距离判别法、Fisher判别法和贝叶斯判别法的异同。

二、

2、设$X$~$N_2$(μ，Σ)，其中$X$ ~ ($X_1$,$X_2$,$X_3$)，μ = (${\mu }_1$，${\mu }_2$)'，Σ = $\left[\begin{array}{cc}{\sigma }_1^2& c\\ c& {\sigma }_2^2\end{array}\right]$

（1）证明$X_1$+$X_2$和$X_1$-$X_2$的充要条件是${\sigma }_1^2$=${\sigma }_2^2$；
（2）试求$X_1$+$X_2$和$X_1$–$X_2$的分布。

---

3、四个变量的距离矩阵如下，试用类平均法对其进行分类，画出聚类图，并给出将其分为两类的结果。

$\left[\begin{array}{cccc}0& & & \\ 2& 0& & \\ 6& 4& 0& \\ 6& 6& 5& 0\end{array}\right]$

---

4、已知6个样品的观测值为：1，4，5，6，9，11。分别用重心法（粗分类按数值大小均分）和密度法选取凝聚点，用K均值法分为3类。

---

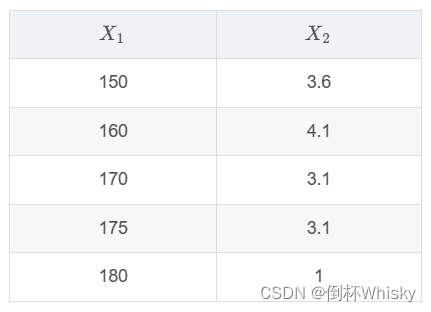
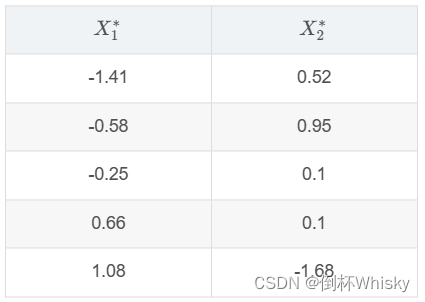
5、五个地区国内生产总值$X_1$和存储量$X_2$和标准化数据如下，求出的相关阵R如下。（1）进行主成分分析；（2）计算每个主成分的贡献率以及每个原始变量的信息提取率；若要求损失代价小于15%，应选取几个主成分？（3）按主成分得分对五个地区进行排序。

$R=\left[\begin{array}{cc}1& -3/4\\ -3/4& 1\end{array}\right]$

---

6、设某总体可用2个指标来描述，在因子分析时计算出的特征值和对应的特征向量如下：

${\lambda }_1$=1.96，$l_1$= (0.63,0.59,0.51)’
${\lambda }_2$=0.64，$l_2$= (-0.22,-0.49,0.84)’

求：
（1）计算因子载荷矩阵$A$，并建立因子模型；
（2）计算共同度$h_i^2$；
（3）计算公共因子对X的贡献。