在上一篇中我们推导了损失函数 J ( θ ) = 1 2 m ∑ i = 1 m ( y i − h θ ( x i ) ) 2 J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (y^{i} - h_{\theta}(x^{i}))^2 J(θ)=2m1∑i=1m(yi−hθ(xi))2的由来,结尾讲到最小化这个损失函数来找到最优的参数 θ \theta θ,通常是使用梯度下降实现的。
梯度下降广泛用于机器学习和统计建模中的参数估计,特别是在训练线性回归模型时。它的目标是最小化一个损失函数(目标函数),这个函数量化了模型预测和真实数据之间的误差。梯度下降通过迭代地调整模型的参数来减少成本函数的值。
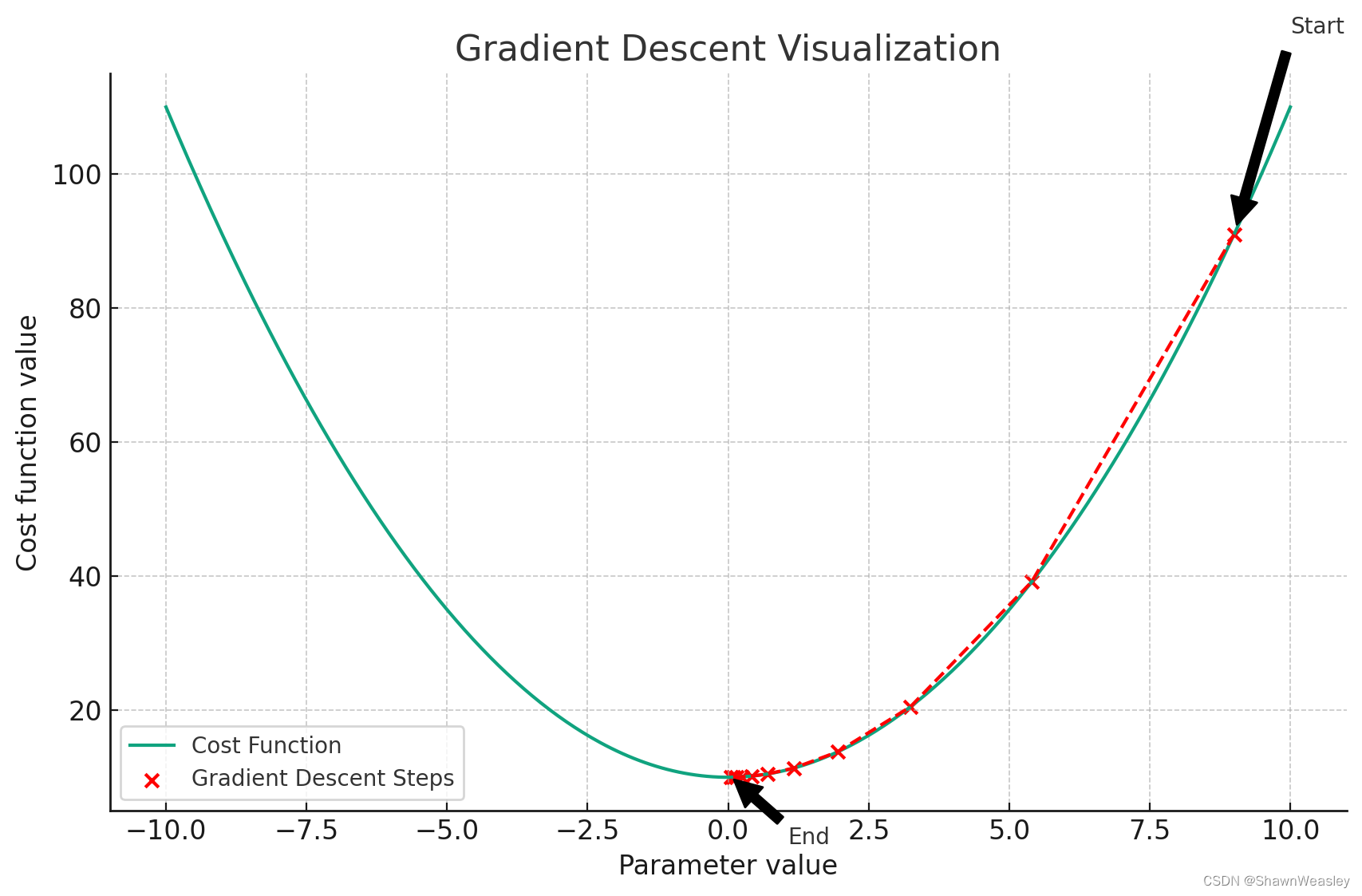
梯度下降的过程类似于一个“盲人下山”的过程:
起始点:就像盲人随机地在山上的某个位置开始,梯度下降算法通常从一个随机的参数值开始。这个起始点可能远离最小值,也就是最低点。
目标值(误差最低值):算法的目标是找到成本函数的最小值,这就好比盲人想要下山到达山谷底部,那里是海拔最低的地方。
获取移动方向:盲人通过脚下的坡度来判断下山的方向,而梯度下降算法通过计算成本函数的梯度来确定下降的方向。梯度告诉我们成本函数上升最快的方向,我们需要往相反方向移动来降低成本函数的值。
控制移动距离(步长):盲人下山时的每一步都不会太大,以免跌倒;同理,梯度下降算法中的学习率决定了每一步下降的距离。学习率太大可能会越过最小值,太小则下降过程会非常缓慢。
递归移动(迭代更新):盲人会一步一步地移动,每走一步都基于当前位置的坡度来决定下一步的方向。梯度下降算法通过迭代地更新参数,每次迭代都基于当前参数的梯度来更新,直到找到最小值或者达到其他停止条件。
在这个下山(梯度下降)概念中,又细分出几种算法,其中如上述的普通梯度下降被命名为:批量梯度下降,除了批量梯度下降外还有随机梯度下降和小批量梯度下降。
批量梯度下降:
批量梯度下降(Batch Gradient Descent)和上述的方法一样,小步多次逐步找到最终的目标值,在每次迭代中使用全部的训练数据来计算损失函数的梯度。因为要用到全部训练数据,所以内存占用高、性能差、速度慢、准确度高。
批量梯度下降的详细步骤:
- 初始化参数:
在开始迭代之前,首先随机选择一组参数 θ \theta θ或者从一个零向量开始。 - 计算梯度:
在每次迭代中,先计算损失函数对于每个参数 θ j \theta_j θj的梯度。这涉及到对整个训练集的计算,如下所示: ∇ θ J ( θ ) = − α 1 m ∑ i = 1 m ( y i − h θ ( x i ) ) x i \nabla_{\theta} J(\theta) = -\alpha \frac{1}{m} \sum_{i=1}^{m} (y^{i}-h_{\theta}(x^{i}) )x^{i} ∇θJ(θ)=−αm1i=1∑m(yi−hθ(xi))xi
其中:
- ∇ θ J ( θ ) \nabla_{\theta} J(\theta) ∇θJ(θ)表示损失函数 J ( θ ) J(\theta) J(θ)关于参数向量 θ \theta θ的梯度
- m m m是训练样本的数量
- x i x^{i} xi是第 i i i个训练样本的特征
- y i y^{i} yi是对应的目标值
- y i − h θ ( x i ) y^{i} - h_{\theta}(x^{i}) yi−hθ(xi)是预测误差,也就是模型对第 i i i个训练样本的预测值 h θ ∗ ( x i ) h_{\theta}* (x^{i}) hθ∗(xi)与实际值 y i y^{i} yi之间的差异
- x i x^{i} xi(第 i i i的特征向量)与预测误差相乘,表示梯度是如何随着特征 x i x^{i} xi的变化而变化
- α \alpha α表示步长
- 更新参数:
计算出梯度后,更新参数 θ : = θ − α ∇ θ J ( θ ) \theta := \theta - \alpha \nabla_{\theta} J(\theta) θ:=θ−α∇θJ(θ)
α 是学习率,决定了在参数空间中移动的步长。
迭代直至收敛:
重复步骤2和步骤3直到损失函数的值不再显著变化,或者达到一定的迭代次数。
所以相对于 θ j \theta_j θj的下一个位置 θ j ′ \theta_j^{\prime} θj′就可以表示为 θ j \theta_j θj减去 ( − 1 m ∑ i = 1 m ( y i − h θ ( x i ) ) x i ) (-\frac{1}{m} \sum_{i=1}^{m} (y^{i}-h_{\theta}(x^{i}) )x^{i}) (−m1∑i=1m(yi−hθ(xi))xi),即:
θ j ′ = θ j + α 1 m ∑ i = 1 m ( y i − h θ ( x i ) ) x j i \theta_j^{\prime} = \theta_j + \alpha \frac{1}{m} \sum_{i=1}^{m} \left(y^{i} - h_{\theta}(x^{i}) \right) x_j^{i} θj′=θj+αm1i=1∑m(yi−hθ(xi))xji
随机梯度下降:
随机梯度下降是批量梯度下降的一个优化版本,每次只找一个样本,迭代速度快,但不一定每次都朝着收敛方向。对于每个参数 θ j ′ \theta_j^{\prime} θj′,更新规则如下:
θ j ′ = θ j + ( y i − h θ ( x i ) ) x j i \theta_j^{\prime}= \theta_j + \left({y^{i} - h_ \theta}(x^{i}) \right) x_j^{i} θj′=θj+(yi−hθ(xi))xji
小批量梯度下降:
小批量梯度下降在每次迭代中使用一个小批量(batch)的样本来计算梯度和更新参数。相当于取少量的数据牺牲一些每次移动的准确性,从而极大提高运算速度,因此也是最常用的梯度下降方法。对于每个参数 θ j ′ \theta_j^{\prime} θj′,更新规则如下:
θ j ′ = θ j − α 1 B ∑ i = k k + B − 1 ( h θ ( x i ) − y i ) x j i \theta_j^{\prime}= \theta_j - \alpha \frac{1}{B} \sum_{i=k}^{k+B-1} \left( h_{\theta}(x^{i}) - y^{i} \right) x_j^{i} θj′=θj−αB1i=k∑k+B−1(hθ(xi)−yi)xji